Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.106 n.11-12 Pretoria Nov./Dec. 2010
http://dx.doi.org/10.4102/sajs.v106i9/10.180
RESEARCH ARTICLE
Repeat-punctured superorthogonal convolutional turbo codes on AWGN and flat Rayleigh fading channels
Narushan Pillay; HongJun Xu; Fambirai Takawira
School of Electrical, Electronic and Computer Engineering, University of KwaZulu-Natal, South Africa
ABSTRACT
Repeat-punctured turbo codes, an extension of the conventional turbo-coding scheme, has shown a significant increase in bit-error rate performance at moderate to high signal-to-noise ratios for short frame lengths. Superorthogonal convolutional turbo codes (SCTC) makes use of superorthogonal signals to improve the performance of the conventional turbo codes and a coding scheme that applies the repeat-punctured technique into SCTC has shown to perform better. We investigated two new low-rate coding schemes, repeat-punctured superorthogonal convolutional turbo codes (RPSCTC) and dual-repeat-punctured superorthogonal convolutional turbo codes (DRPSCTC), that make use of superorthogonal signaling, together with repetition and puncturing, to improve the performance of SCTC for reliable and effective communications. Simulation results in the additive white Gaussian noise (AWGN) channel and the frequency non-selective Rayleigh fading channel are presented together with analytical bounds of bit error probabilities, derived from transfer function bounding techniques. From the simulation results and the analytical bounds presented, it is evident that RPSCTC and DRPSCTC offer a more superior performance than SCTC in the AWGN channel, as well as in flat Rayleigh non-line-of-sight fading channels. The distance spectrum is also presented for the new schemes and accounts for the performance improvement rendered in simulations. It is important to note that the improved performance that SCTC, and consequently RPSCTC and DRPSCTC, exhibit is achieved at the expense of bandwidth expansion and complexity and would be ideal for power-limited satellite communication links or interference-limited systems.
Keywords: puncturing; repetition; superorthogonal convolutional turbo codes; turbo codes; Walsh-Hadamard
INTRODUCTION
Modern digital cellular systems employ some form of channel coding to improve bit-error rate (BER) performance. Convolutional coding is the most widely used in these systems. However, operating at high signal-to-noise ratios (SNRs) requires larger antennas and bandwidths to be used, resulting in a large link budget. In the early 1990s, turbo codes (TCs) were introduced by Berrou et al.1, who showed their performance to be a few tenths of a decibel (dB) from Shannon's theoretical limit. Typically, for large frame lengths, for example N = 16 384, SNRs, Eb/N0, of -0.15 dB at a BER level of 10-3 have been reported.1,2,3 TCs have three enhancements in the coding area, namely the use of recursive systematic convolutional codes, random interleaving and the separation of intrinsic and extrinsic information in the decoder for cooperation. The performance of TCs improves with increasing interleaver size, due to the larger interleaver gain.3,4 However, increasing the interleaver size requires a simultaneous increase in the information frame length, because the interleaver size is set identically to the information frame length for the conventional TC, which makes it difficult to use TCs in applications that demand low-transmission delays, such as real-time voice communications. An error floor manifests in the BER performance of TCs because of the presence of low-weight codewords with small multiplicities. Several techniques have been proposed to lower the error floor,4,5,6,7,8,9 one of which is to use a repeat-punctured structure in the second parity branch of the conventional TC scheme.4 The repeat-punctured TC scheme proposed by Komulainen and Pehkonen not only increases the interleaver size, but also enlarges the low-weight codewords.4 Repeat-punctured turbo codes (RPTC) have shown a significant increase in performance at moderate to high SNRs.4 For example, for an information frame length N = 1024, simulation results have shown that the RPTC scheme has an approximate 2 dB coding gain over the conventional TCs, at a BER level of 10-5.
Superorthogonal convolutional turbo codes (SCTC), introduced by Komulainen and Pehkonen4, is a low-rate coding scheme that is suitable for code spreading, for achieving coding gain and bandwidth expansion in direct-sequence code-division multiple access systems and for automatic repeat-request systems with partial retransmission.3,4,5 SCTC exhibits an improved performance over the classical turbo coding algorithm. For a small frame length (e.g. N = 200) and a constraint length K = 4, Eb / N0 values of approximately 0.7 dB at a BER level of 10-3 have been reported. Motivated by the improved performance of RPTC, we investigated the performance of repeat-punctured superorthogonal convolutional turbo codes (RPSCTC). We can go one step further and include repetition and puncturing on both branches of the encoder. A scheme that utilises this configuration is referred to as dual-repeat-punctured superorthogonal convolutional turbo codes (DRPSCTC). Both of the above schemes use orthogonal signaling and parallel concatenation, together with repetition and puncturing, to improve the performance of SCTC for reliable and effective communications. Simulation results in the additive white Gaussian noise channel and the flat Rayleigh fading (FRF) channel are presented together with analytical bounds of bit error probabilities, derived from transfer function bounding techniques. The distance spectrum is also presented for the new scheme and compared to the low-rate SCTC scheme.
The paper is organised as follows: firstly, the concept of RPSCTC together with the encoding and decoding structures is introduced. We then present the DRPSCTC scheme and evaluate the performance on the AWGN channel and the FRF channel. Thereafter we present some analysis followed by the simulation results for memory depths, m = 2 and m = 4, together with their analytical BER bounds for AWGN and FRF channels and the codeword distance spectrum.
REPEAT-PUNCTURED SUPERORTHOGONAL CONVOLUTIONAL TURBO CODES
Encoder
Orthogonal, bi-orthogonal and superorthogonal convolutional codes are well documented.4,10 For an orthogonal convolutional encoder, all of the possible output sequences per branch of the trellis are mutually orthogonal. If we enlarge the orthogonal signal set to incorporate their complementary sequences, we have a bi-orthogonal signal set that has twice as many members for the same sequence length. By taking advantage of this extended set, we can have a bi-orthogonal convolutional code.3 That is, all of the encoder output sequences that leave the same state are antipodal. For superorthogonal codes, all of the encoder output sequences that either leave the same state or merge within the same state are antipodal and only one sequence and its complement are needed for every two states of the trellis. Many methods for generating the orthogonal signal set exist; one possible choice for generating the set of orthogonal sequences is the Walsh functions, which can be obtained from Hadamard matrices.3,4,10 A SCTC is simply a parallel concatenation of superorthogonal recursive convolutional codes (SRCC).
Spectral thinning is primarily responsible for the near Shannon-capacity performance of TCs and consequently the performance of the schemes presented in this paper. This phenomenon ensures that the constituent codes in the conventional TC do not produce low-weight codewords simultaneously, which is achieved through the use of the pseudorandom interleaver in the conventional TCs. The information bits are first permuted by the interleaver and then encoded by the second component encoder, reducing the probability of both component recursive systematic convolutional encoders producing low-weight codewords at their outputs. The phenomenon of spectral thinning is demonstrated in Figure 1. It can be seen that, as the interleaver length B is increased towards infinity for hypothetical distance spectra, the distance spectrum begins to 'thin' for low-weight codewords. It is important to note that this thinning of the distance spectrum allows the free-distance asymptote of a TC to dominate the performance for lower SNRs and thus achieve near Shannon-capacity performance.11

RPTCs were introduced by Kim et al.12, who made use of a repeat-puncture mechanism to exploit the fact that larger interleavers increase the BER performance of the conventional TC.3,4,12,13 In the conventional TC, the information frame length is set identically to the interleaver size, such that if we want to increase the interleaver size then we need to pass larger frames of information into the encoder. However, larger information frames correspond to larger processing delays, both in the encoder and the decoder and would not be tolerable in many applications, such as real-time voice communications. RPTCs employ a repetition operation block prior to interleaving, which allows for small frame lengths and larger interleavers to be used in the same system. Simulations show an improved performance over the classical TCs for moderate to high SNRs.12 With a pseudorandom interleaver, the weight-2 input sequence is known to produce low-weight codewords for the conventional TC. However, with RPTC, a weight-2 input sequence becomes a weight-2T input sequence, where T represents a repetition index. This significantly improves the performance of the TC, because the probability of the second constituent encoder producing a low-weight codeword is reduced, as a result of the recursive nature of the component encoders.
Figure 2 shows the structure of the RPSCTC encoder. Similar to the conventional SCTCs, the RPSCTC encoder consists of two parallel concatenated SRCCs. As an example, a more detailed diagram with memory m = 4 is depicted in Figure 3. The first parity sequence



is produced from the first constituent code, SRCC 1, with an input data frame of length N. Because the parallel concatenated code is made up of superorthogonal recursive convolutional component codes, the length of the first parity sequence is 2m-1N for an input frame length N,4,10 and thus corresponds to a rate:

However, unlike the conventional TC, where the input data frame of length N is directly permuted by an interleaver of length N, the input data frame of length N is first repeated T times and thereafter interleaved by an interleaver, π, of length TN. The second parity sequence:

is produced from the second constituent code, SRCC 2, with an interleaved data frame of length TN as input and in the same manner corresponds to a rate:

The total code rate for RPSCTC is therefore:

When we puncture, the objective is for T to look like unity. In this paper, a repetition factor of T = 2 was used, however, T can be increased to lower the code rate even further, or to generate a series of rate-compatible codes. The distance spectrum shows that an RPTC with T = 3 has slightly more codewords at the low-weight end of the spectrum than when T = 2.12 This difference is as a result of the excessive puncturing required when T = 3. In addition, it is important to note that as T is increased, the computational complexity also increases.
In the case of RPSCTC and SCTC, there is no common channel output stream as in the case of conventional TCs because the systematic information bit is not explicitly sent via the channel – but with appropriate mapping of the Walsh functions, the outputs can be made systematic. Komulainen and Pehkonen explain how the recursive nature of a code leads to the codewords being systematic in the case of SCTC.4,10 As a repetition factor, T = 2, was employed prior to producing the second parity sequence, we are at liberty to puncture every second bit out of every T bits from the Walsh sequence (punctured bits are replaced by a dummy bit '0' at the receiver, representing an erasure) in order to recover the loss in code rate (Figure 4). In Figure 4, punctured bits are represented by the positions of the shaded blocks. One of the bits in the first parity sequence was punctured to increase the code rate to R = 1/15. These positions also represent the positions where dummy bits would be inserted at the receiving end. Puncturing causes a drop in the performance of the code; however, further puncturing strategies could be investigated to minimise this drop in performance.

The punctured second parity sequence is then transmitted together with the first parity sequence to the receiver front-end. The Walsh-Hadamard generator, shown in exploded view of SRCC 1 or SRCC 2 in Figure 3, uses Walsh functions obtained from Hadamard matrices to generate the orthogonal sequences. The Walsh-Hadamard generator can be, simply, a lookup table with the superorthogonal output sequences. For memory, m = 4, corresponding to Figure 3, the Hadamard matrix,

and its complementary matrix,

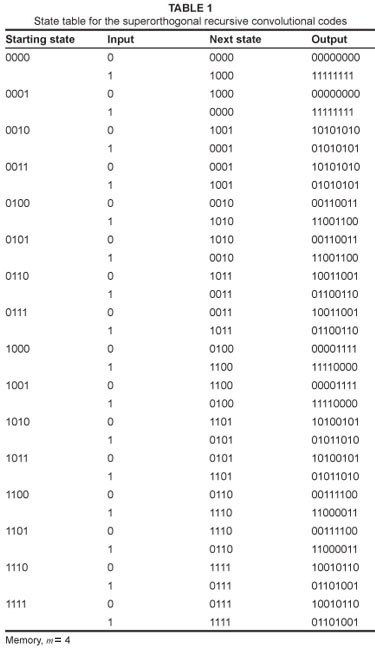
need to be considered, as shown in Figure 5, where all the row and column sequences are Walsh sequences. Table 1 shows the state table for the SRCC with memory depth, m = 4, where the output sequences are Walsh sequences.

Corresponding to an input information stream,

the output from SRCC 1 is

and the output from the second constituent encoder prior to puncturing is

The general structure of a SCTC encoder is derived in Box 1. All states are fed back to the input, making the structure recursive or an infinite impulse response. If necessary, one of the bits of the Walsh sequences can be punctured, similarly to ordinary TCs, to increase the code rate. The manner in which the trellis is terminated has an effect on the performance of the SCTCs, similar to classical TCs. The technique for trellis termination is outlined by Robertson.14
Decoder
Unlike the Viterbi algorithm, which finds the most likely sequence to have been transmitted, the maximum a posteriori (MAP) algorithm determines the most likely information bit to have been transmitted at each bit time k. Using a posteriori probabilities, for a small probability of bit error (Pb), the performance difference between MAP and soft-output Viterbi algorithm (SOVA) is very small. However, at low Eb / N0 and high Pb values, MAP outperforms the latter.13 The well-known MAP algorithm proceeds somewhat like the Viterbi algorithm, but in two directions, forward and backward, over a block of code bits.2,8,13,15 Similarly to the conventional TCs, RPSCTC uses the MAP algorithm in each of the component decoders.
The decoding structure shown in Figure 6 makes use of an iterative technique, together with serial concatenation of the constituent decoders. An outer decoder, Decoder 1, and an inner decoder, Decoder 2, in cooperation produce soft decisions that are converted into extrinsic log-likelihood ratios (LLRs) that are mutually exchanged, thus increasing the reliability of the resulting decisions. In the first step of the decoding for RPSCTC, the punctured, corrupted first parity sequence from the channel is sent to Decoder 1.

Because the sequence was punctured before transmission, dummy bits now need to be added and, similarly, for the second parity sequence. Figure 7 illustrates the manner in which the dummy bits are added at the input of the decoder. The lightly shaded, dash-outlined blocks represent positions at which bits were punctured to increase the code rate. Before either corrupted parity sequence is sent to a component decoder, dummy bits, '0', are introduced into these positions.

These introductions serve to reconstruct the original parity sequences prior to puncturing at the encoder. The reconstructed first parity sequence [Sqn 3] is sent to the first decoder, Decoder 1. Decoder 1 assumes zero a priori information and uses the MAP algorithm to yield N soft LLRs, L1(dk | y), at its output. These LLRs need to be converted into N extrinsic decisions, which can be used to assist the second decoder, Decoder 2, in its LLR computations. Taking into account the channel measurement and zero a priori information, the extrinsic information is computed in a manner similar to that used in the conventional TC. At this point, it is important to consider Decoder 2's initial processing. The reconstructed second parity sequence [Sqn 4] is fed into Decoder 2. Because Decoder 2 is operating on enlarged sequences, the a priori information assigned to Decoder 1's extrinsic output has to be enlarged. These N extrinsic decisions from Decoder 1,

are first repeated T times to yield,

This process yields the extrinsic decisions, which are of the same form as the original input message sequence. Earlier it was pointed out that the second parity sequence from the encoder contained systematic bits, but in a permuted form. It is thus important to interleave the repeated extrinsic sequence,

before input to Decoder 2. Decoder 2 now uses this second input to improve the reliability of its computation of

These TN soft LLRs are routinely converted into TN extrinsic decisions,

The extrinsic decisions are then de-interleaved

and the de-interleaved sequence is averaged according to [Eqn 8] to produce N de-interleaved extrinsic decisions,

where i = 0, 1, 2, 3. The process of averaging is responsible for a performance improvement in the decoding, since TN decisions from Decoder 2 are being converted into N decisions and this averaging mechanism is continuously working to improve the reliability of the assist information to Decoder 1. The mutual exchange of extrinsic information in the overall decoder is iterated several times. After a sufficient number of iterations, the soft output from Decoder 2,

is de-interleaved and averaged similarly to [Eqn 8] to yield N soft decisions. The soft decisions are then converted into hard decisions, that is, the estimate of the original message sequence.
DUAL-REPEAT-PUNCTURED SUPERORTHOGONAL CONVOLUTIONAL TURBO CODES
Encoder
The dual-repeat-punctured superorthogonal convolutional turbo codes (DRPSCTC) scheme is an extension of the RPSCTC scheme. A simple modification to the structure, that is, dual repetition, can further improve the performance. The structure of the encoder for DRPSCTC is shown in Figure 8.

The structure is almost identical to the encoder used for RPSCTC, with the major difference being that a repetition block is used prior to encoding both parity sequences. The message sequence of length N is first sent through a repeater structure which enlarges the sequence to TN entries. On their respective branches, the enlarged sequences are interleaved and then encoded with superorthogonal signals to yield sequences of length 2m-1TN. To control the code rate, the sequences need to be punctured using a special technique.
The aim of the special puncturing technique is to puncture the sequences at the same rate used to investigate the low-rate RPSCTC and SCTC schemes, so that comparisons can be made between these schemes. Figure 9 illustrates the technique employed in the puncturing of DRPSCTC-coded outputs. For memory m = 4 and repetition index T = 2, there should be 2m-1TN, bits at the output of the branch for every input bit (i.e. 16 bits), which equates to a total of 32 bits


at the output for two parity sequences (Figure 9). The completely shaded blocks in Figure 9 represent the bits that are punctured. One bit still requires puncturing to increase the code rate to
R = 1/15. On the right side of Figure 9, two bits, represented by the hatched blocks, are monitored for a '+1' or a '−1', respectively. The first of these two bits is punctured if a '+1' is detected. However if a '+1' is not found, then the second of these two bits is checked for a '−1' and punctured correspondingly. In the event of both these bits holding the opposite value (a probability of 0.25), then both these bits are punctured, which is still on average effectively a code rate of R = 1/15.
Decoder
The decoder for DRPSCTC is similar to the structure of the decoder for RPSCTC. However, there is no explicit systematic output in the DRPSCTC decoder, thus eliminating the need for interleaving at the input. Firstly, the sequences need to be reconstructed before being sent to the constituent decoders. Figure 10 illustrates how the sequences are reconstructed. On reception of the parity sequences, the lengths of each of these sequences need to be checked to determine which sequence was punctured for an extra bit. If the first parity sequence is only shorter by one bit, then a '+1' is introduced into the sequence. Similarly, if the second parity sequence is found to be the shorter sequence, then a '−1' is introduced. Alternatively, if both sequences are short by a single bit, then a '−1' is introduced into the first sequence and a '+1' is introduced to the second. This technique eliminates any probability of error of this bit, represented by the hatched, dash-outlined blocks in the right portion of the diagram. At this point, each of the parity sequences should be of length 2m-1N. Next, dummy bits '0' are inserted into previously punctured bit positions, which are indicated by the lightly shaded, dash-outlined blocks in Figure 10.

The structure of the decoder of DRPSCTC is shown in Figure 11. In the first iteration, Decoder 1 has a single input: the corrupted first parity sequence reconstructed to length 2m-1TN. Using this input the MAP algorithm is used to generate soft LLRs


at the decoder output. Note that the soft LLRs are in a π1 permuted format and are thus denoted by a single dash. [Sqn 12] is then converted into soft extrinsic information

in a manner similar to the conventional turbo decoding and the ensuing schemes are discussed. This extrinsic information is de-interleaved by the first interleaver mapping, then interleaved by the second interleaver mapping. It is important to note that the order of interleaving and de-interleaving here depends on the order of interleaving done within the encoder. The resulting sequence of scrambled extrinsic decisions is then followed by averaging and repetition to improve the reliability of the assist information to Decoder 1. Decoder 2 takes two inputs, namely the a priori information sent from Decoder 1 and the second corrupted parity sequence with dummy bits in previously punctured positions, to produce soft LLRs

in a π2 permuted format. The extrinsic sequence

is then de-interleaved by the second interleaver mapping to yield [Sqn 9], which is then permuted by π1.
These TN elements are then averaged and repeated T times to produce a priori information suitable for improving the error performance of Decoder 1. Averaging is performed similarly to the method described for the RPSCTC scheme in [Eqn 8]. After the mutual exchange of information between the decoders is iterated several times, the soft output from Decoder 2 is de-interleaved

then averaged to yield N soft decisions, which are converted into hard decisions to yield an estimate of the original message sequence.
MAXIMUM-LIKELIHOOD PERFORMANCE BOUNDS
There are two main tools for the performance evaluation of TCs: computer simulation and the standard union bounds. Computer simulation generates reliable probability of error estimates as low as 10-6 and is useful for rather low SNRs, because the error probabilities for larger SNRs are too small to simulate. The union bound provides an upper bound on the performance analysis of RPSCTCs and DRPSCTCs with maximum-likelihood decoding averaged over all possible interleavers.
The union bounds for the RPSCTC and DRPSCTC schemes are all evaluated using the same transfer function method discussed by Divsalar et al.16 and by Xu and Takawira5. In this section, we need only present the expressions for the encoders for the RPSCTC and DRPSCTC schemes.
For RPSCTC, the probability of producing a codeword fragment of weight d given a randomly selected length N input sequence of weight i for Encoder 1 is given by

and by

for Encoder 2, where t(•) is the transfer function for the constituent encoder obtained by using the technique presented by Divsalar et al.16, d1 and d2 are the codeword weights for Encoder 1 and Encoder 2, respectively and the denominator in [Eqn 10] and [Eqn 11] represents the total number of codewords for information weight i and Ti, respectively.
As a result of the dual structure for DRPSCTC, both component encoders take as input a message block of length TN. Thus the probability of producing a codeword of weight d conditioned on a weight i input sequence is given by

where q = 1 for Encoder 1 and q = 2 for Encoder 2.
The codeword distance spectra are given by

for RPSCTC and

for DRPSCTC; where

represents the number of codewords of SRCC1 where the input sequence is of weight x and the output parity sequence is of weight y and

is represented similarly. These coefficients can be obtained using the techniques employed by Komulainen and Pehkonen4, and by Kim et al.12
The union bound can then be obtained from
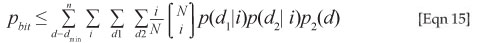
where the two-codeword probability for the AWGN channel is denoted by

where Q(.)is the Q-function and R is the rate of the code and
Eb / N0 is the SNR.
For application of the union bound to Rayleigh fading channels,10,17,18,19 two-codeword probability is necessary. The two-codeword probability, p2(d), with channel state in fully-interleaved channel is obtained by

SIMULATION RESULTS
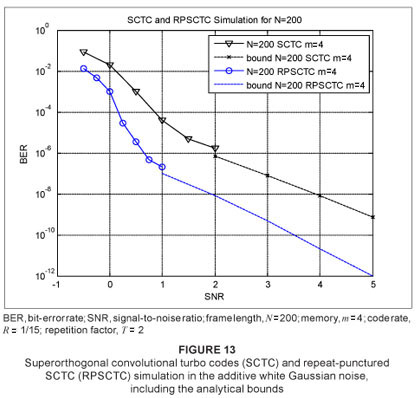
In order to investigate the performance of RPSCTC and DRPSCTC, we simulated the schemes in the AWGN channel and the flat Rayleigh non-line-of-sight (NLOS) fading channel. An input frame of length N = 200 was used. A uniform interleaver was chosen and a straightforward puncturing pattern was employed, although other extravagant patterns could be investigated to yield better performances. For the decoder, 18 iterations were chosen, although this could be decreased at higher SNRs to shorten simulation time without compromising on accuracy. SNR has been previously defined for AWGN and Rayleigh fading channels13,19,20,21 The simulation results for the AWGN channel are illustrated in Figure 12 for memory m = 2 and code rate R = 1/3 (punctured from R = 1/4 to R = 1/3) and in Figure 13 for memory m = 4 and code rate R = 1/15 (punctured from R = 1/16 to R = 1/15). The performance curves are shown converging to the bounds. It can be seen that a coding gain of approximately 0.5 dB was achieved at a BER level of 10-3 and a coding gain of almost 1.5 dB was achieved at a BER level of 10-6 for a constraint length K = 3.

Rayleigh fading is a statistical model for the effect of a propagation environment (or the heavy build-up of urban environments) on a radio signal and is a reasonable model for tropospheric and ionospheric signal propagation.
For NLOS between the transmitter and receiver, the scheme was also simulated in a Rayleigh fading channel, the results for which are presented in Figures 14 and 15. Again, the measure of quality of service chosen is a plot of BER versus SNR. As a stopping criterion for the simulations for both SCTC and RPSCTC, 150 frame errors were used. The velocity used for the moving receiver was vc = 50 km/h and a fc = 2 GHz carrier frequency was used with Doppler frequency fd given by [Eqn 18]. The speed of light c is 3 x 108 m/s.



Again, a frame length of N = 200 was considered at a code rate of R = 1/15. An SNR range of 2 dB –11 dB was considered so that the performance for low probability of errors could be investigated. A coding gain of almost 1 dB was achieved throughout the SNR range of SCTC and RPSCTC.
Simulation results for NLOS channels (modelled by the Rayleigh distribution) are exemplified in Figures 14 and 15. For frequency non-selective (FRF) channels with side information, a coding gain of approximately 0.5 dB was achieved at all BER values.
Figure 16 shows the simulation in the AWGN channel for DRPSCTC for a frame length N = 200, memory m = 4 and code rate R = 1/15, supported by its bound. The BER versus SNR for DRPSCTC is plotted together with the simulations for RPSCTC and SCTC for memory m = 4 with their bounds. It can be seen that, as the SNR increases, the performance of DRPSCTC starts to improve, in comparison to RPSCTC. The turning point for this scenario can be seen at approximately 0.2 dB.
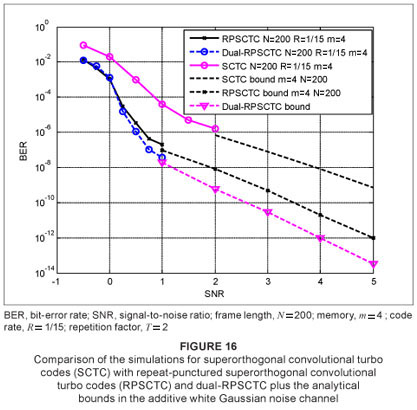
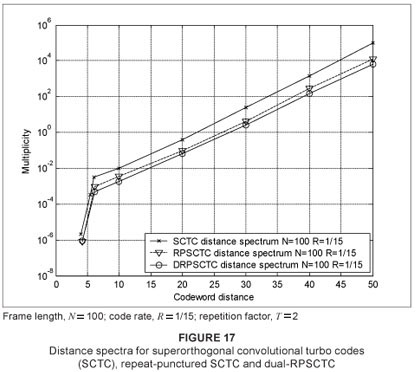
Figure 17 depicts the codeword distance spectra of the SCTC, RPSCTC and the DRPSCTC schemes with multiplicity on the ordinate axis and codeword distance on the abscissa axis. The distance spectrum verifies the performance improvement shown in the previous graphs (Figures 12–16). It can be seen that the number of codewords with low weights (small distances, d) has been decreased and the spectrum has been shifted to the right as a result of the presence of a larger number of high-weight codewords.
CONCLUSION
We have presented the results for two new schemes, RPSCTC and DRPSCTC, simulated in the AWGN and the FRF channels and presented together with their union bound, based on maximum-likelihood, derived from transfer function bounding techniques and the codeword distance spectrum. From the simulations and the analytical bounds presented, it is evident that RPSCTC and DRPSCTC offer a superior performance to that of SCTC in the AWGN channel, as well as in NLOS channels. The codeword distance spectrum that was presented motivates for this performance improvement. It is important to note that the improved performance that SCTC, and consequently RPSCTC and DRPSCTC, exhibit is achieved at the expense of bandwidth expansion and complexity and would be ideal for power-limited satellite communication links or interference-limited systems. One of the drawbacks of SCTC, RPSCTC and DRPSCTC would be the fact that the rate of the code is exponentially related to the memory depth of the constituent encoders used. Thus many more extravagant puncturing strategies could be investigated to yield better BER performances. In addition, the low-rate coding schemes presented above can be compared with low-rate turbo-Hadamard codes.
REFERENCES
1. Berrou C, Glavieux A, Thitimajshima P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. Paper presented IEEE International Conference on Communications. Proceedings of IEEE International Conference on Communications; IEEE Xplore; 1993 May 23–26; Geneva, Switzerland. New York: IBM Corporation; 1993. vol. 2, p. 1064–1070. [ Links ]
2. Divsalar D, Pollara F. Multiple turbo codes for deep-space communications. The Telecommunications and Data Acquisition Progress Report 42121. Pasadena: Jet Propulsion Laboratory, 1995; p. 66–77. [ Links ]
3. Leanderson CF. Low-rate turbo codes. Project report SE-221 00. Lund: Lund University; 1998. [ Links ]
4. Komulainen P, Pehkonen K. A low-complexity superorthogonal turbo-code for CDMA applications. Paper presented IEEE International Symposium on Personal, Indoor and Mobile Radio Communications; 1996 Oct 15-18; Taipei, Taiwan. New York: ROC; 1996. vol. 2, p. 369–373. [ Links ]
5. Xu H, Takawira F. Performance bounds of turbo codes with redundant input. Project Report, School of Electrical and Computer Engineering, Inha University, Korea, and Guilin Institute of Electronic Technology, PR China; School of Electrical and Electronic Engineering, University of Natal, South Africa, 2003. [ Links ]
6. Anderson JD. Turbo codes extended with outer BCH code. Electron Lett. 1996;32(22):2059–2060. [ Links ]
7. Benedetto S, Montorsi G. Performance evaluation of parallel concatenated codes. Paper presented IEEE International Conference on Communications; 1995 June 18–22; Seattle, USA. New York: IBM Corporation; 1995. vol. 2, p. 663–667. [ Links ]
8. Bahl LR, Cocke J, Jelinek F, Raviv J. Optimal decoding of linear codes for minimizing symbol error rate. IEEE Trans Inf Theory. 1974;IT20:284–287. [ Links ]
9. Narayanan KR, Stuber GL. Selective serial concatenation of turbo codes. IEEE Commun Lett. 1997;1(5):136–138. [ Links ]
10. Komulainen P, Pehkonen K. Performance evaluation of superorthogonal turbo codes in AWGN and flat Rayleigh fading channels. IEEE J Sel Areas Commun. 1998;16(2):196–205. [ Links ]
11. Perez LC, Seghers J, Costello Jr DJ. A distance spectrum interpretation of turbo codes. IEEE Trans Inf Theory. 1996;42(6):1698–1709. [ Links ]
12. Kim Y, Cho J, Oh W, Cheun K. Improving the performance of turbo codes by repetition and puncturing. Project Report, Division of Electrical and Computer Engineering, Pohang University of Science and Technology. [ Links ]
13. Sklar B. Digital communications. Fundamentals and applications. Beijing: Publishing House of Electronics Industry; 2001. [ Links ]
14. Robertson P. Illuminating the structure of code and decoder of parallel concatenated recursive systematic (turbo) codes. Paper presented IEEE Globecom. Proceedings of IEEE Global Telecommunications Conference; The Global Bridge; 1994 Nov 28 -Dec 02; San Francisco, CA. New York: IBM Corporation; 1994. vol. 3, p. 1298–1303. [ Links ]
15. Viterbi AJ. An intuitive justification and a simplified implementation of the MAP decoder for convolutional codes. IEEE J Sel Areas Commun. 1998;16(2):260–264. [ Links ]
16. Divsalar D, Dolinar S, Pollara F. Transfer function bounds on the performance of turbo codes. TDA Progress Report 42122, Communications Systems and Research Section; California Institute of Technology, Aug 1995, p. 44–55. [ Links ]
17. Hall EK, Wilson SG. Design and performance analysis of turbo codes on Rayleigh fading channels. Paper presented Conference on Information Sciences and Systems; 1996 Mar 20-22; New Jersey, USA. [ Links ]
18. Chatzigeorgiou I, Rodrigues MRD, Wassell IJ, Carrasco R. Pseudo-random puncturing: A technique to lower the error floor of turbo codes. Int Symp Inf Theory. 2007:656–660. [ Links ]
19. Qi J. Turbo code in IS-2000 code division multiple access communications under fading. MSc thesis, Kansas, Wichita State University, 1999. [ Links ]
20. Ould-Cheikh-Mouhamedou Y, Crozier S. Improving the error rate performance of turbo codes using the Forced Symbol method. IEEE Commun Lett. 2007;11(7):616–618. [ Links ]
21. Hall EK, Wilson SG. Design and analysis of turbo codes on Rayleigh fading channels. IEEE J Sel Areas Commun. 1998; 16(2):160–174. [ Links ]
 Postal address:
Postal address:
School of Electrical, Electronic and Computer Engineering
University of KwaZulu-Natal, Howard College campus
King George V Avenue
Durban 4041, South Africa
Received: 22 Dec. 2009
Accepted: 11 July 2010
Published: 18 Nov. 2010
Correspondence to: Narushan Pillay
email: pillayn@ukzn.ac.za
This article is available at: http://www.sajs.co.za
© 2010. The Authors. Licensee: OpenJournals Publishing. This work is licensed under the Creative Commons Attribution License.














