Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.106 n.7-8 Pretoria Jul./Aug. 2010
RESEARCH LETTER
The use of a genetic algorithm in optical thin film design and optimisation
Efrem K. EjiguI; Beartys M. LacquetII
IDepartment of Electrical and Electronic Engineering Science, University of Johannesburg, South Africa
IIFaculty of Engineering and the Built Environment, University of the Witwatersrand, South Africa
ABSTRACT
We used a genetic algorithm in the design and optimisation of optical thin films and present the effects of the choice of variables, refractive index and optical thickness, in both applications of this algorithm, in this paper. The Fourier transform optical thin film design method was used to create a starting population, which was later optimised by the genetic algorithm. In the genetic algorithm design application, the effect of the choice of variable was not distinct, as it depended on the type of design specification. In the genetic algorithm optimisation application, the choice of refractive index as a variable showed a better performance than that of optical thickness. The results of this study indicate that a genetic algorithm is more effective in the design application than in the optimisation application of optical thin film synthesis.
Keywords: crossover; Fourier transform; genetic algorithm; merit value; mutation; optimisation; starting population
INTRODUCTION
The subject of designing optical thin films has been abundantly researched over two decades and a number of design and optimisation methods in thin film synthesis have been developed.1,2,3 A genetic algorithm has mainly been used as an optimisation tool, rather than as a designing tool, in applications other than optical thin films. A great deal of research is thus needed to apply a genetic algorithm efficiently to optical thin film synthesis.
The effect of the choice of variables in genetic algorithm design and optimisation applications is very interesting to investigate because of the change in performance of the genetic algorithm, according to the choice of the variable of the thin film; different optical thin film parameters taken as a variable result in a different quality of the final design and optimisation solution. The aim of this study was twofold, (1) to show the effect of the choice of variables in genetic algorithm thin film design and optimisation and (2) to discover in which application the genetic algorithm performs better. A number of variables from the optical properties of thin films can be considered in this regard, but, in this study, only the refractive index and optical thickness were considered. The reason behind the selection of these two thin film variables is the fast effect they have in the change of the phase thickness of the thin film during optimisation. The effect of using the refractive index or optical thickness as a variable is discussed by studying the performance difference between the final design and the desired design.
This paper is structured as follows:
• Firstly, we discuss the theoretical background of genetic algorithms and the use of the Fourier transform in optical thin film design and optimisation.
• Secondly, we present the effect of the choice of variables in genetic algorithm design and optimisation application by considering a reflector design as an example, before comparing several genetic algorithm applications.
• Lastly, we conclude the findings of the study.
THEORETICAL BACKGROUND
Fourier transform design
Fourier transform is an analytical optical thin film synthesis method in which it is possible to relate the spectral transmittance of an inhomogeneous layer to its refractive index profile n(x) by the following expressions4:

where

and k is a wave number calculated as:

in which λ is the wavelength.
In [Eqn 1] x is twice the optical distance from the geometrical centre and is given by:

in which u is the physical distance from the geometrical centre.
The variable Q in [Eqn 1] is a suitably even function of the desired transmittance and is given by different forms, one of which is4,5,6:

where T is the desired design transmittance.
In [Eqn 1] Φ is the phase function, which is suitably odd and given by different forms4,5:

where N is a real number between 1 and 5.
No exact phase value is available and so the phase function represented by [Eqn 5] was chosen from the available forms because using it results in a better final refractive index solution.
By applying the Fourier transform in [Eqn 1] and integrating it with respect to x, the value of n(x) is thus found to be:

Genetic algorithm design
A genetic algorithm is an evolutionary algorithm whereby an optimal solution can be found to an optimisation problem and is different from the classical optimisation methods in several ways.1,3,7 It functions on the principles of evolution found in nature and imitates the process of survival of the fittest.8,9 A genetic algorithm gives a solution to an assigned variable by optimising the solution that is produced from the created starting population. The starting population of a certain size can be created from the variable by evaluating all the options available. In the case of genetic algorithm thin film design, the variable can either be refractive index or optical thickness.7 The variables can also have previously evaluated values or can be constructed from values to which a boundary value is assigned. The Fourier transform, or any other thin film design method, can be used in order to evaluate the variables in the starting population.2 Once the starting population is created, the genetic algorithm can be used to create new solutions, through crossover and mutation, to combine and select the most suitable new solution.7,10 The genetic algorithm design procedure is discussed in detail by Cusick et al.9 and Ejigu and Lacquet11.
The genetic algorithm toolbox and Fourier transform12,13 are used randomly and analytically to create a starting population of refractive index or optical thickness variables, respectively. Firstly, the refractive index is varied within the boundary of 1.7 (low, L) and 3.2 (high, H), while the optical thickness of each layer is kept uniform at 0.066 µm. Secondly, the optical thickness is varied within the boundary of zero and quarter wavelengths, while the refractive index profile is set in the form of a HLH......LH multilayer representation. The high and low refractive index materials selected are applicable within the desired design wavelength range. A multilayer structure of a two-material system is constructed by arranging one material on top of the other, depending on the design across the thickness, for instance, in the HLH......LH/LHL......HL form.
The merit value (MF) is used to represent the difference between the desired transmittance and the computed transmittance over a range of wavelengths and is given by1:
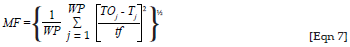
The MF is computed by using the multilayer matrix method. In [Eqn 7] TO and T are the desired and computed transmittances respectively, while WP is the total of wave number points. In this case, 100 points are considered, while j is the iteration number at which the summation is done and tf is a tolerance factor to be set, which, in [Eqn 7], is 0.01.
For this study, a Matlab computer code was generated using the genetic algorithm toolbox14 for the genetic algorithm analysis, while another code was generated for the Fourier transform by using [Eqn 1] to [Eqn 6]. The transmission spectrum was analysed by a Matlab code that used the matrix method.15
METHODS AND RESULTS
In order to show the effect of the choice of variable, a reflector with the following properties was considered: reflectance of >99% at 0.98 µm central wavelength, a bandwidth of 0.20608 µm and an overall optical thickness of 13 µm. The reflector was designed in the wavelength range of 0.7 µm - 1.3 µm by using the genetic algorithm. The genetic algorithm was used to optimise the same kind of reflector, with a rejection band in the range of 0.88182 µm - 1.0879 µm, designed by Fourier transform. In each case, two designs were investigated to determine, (1) the effect of the variables and (2) which genetic algorithm applications performed better in optical thin film synthesis.
Optimisation by genetic algorithm
The optimisation was carried out on the designs of the Fourier transform in two ways.
The first optimisation was on a refractive index starting population size of 150. The genetic algorithm was run for 15 000 generations and the resulting spectral performance is displayed in Figure 1.

The result obtained from this optimisation explains the behaviour of the effect of the refractive index as a variable. The rejection region of the spectral performance was within a bandwidth of 0.2965 µm, which was 9.042% wider than the desired design. The depth of the central wavelength was 0.06951, which was 6% lower than desired, while the full width at half maximum (FWHM) was 0.2182 µm, which was almost equal to that which was desired. The central wavelength point shifted by 1% to 0.99 µm. There were five peaks outside the rejection band: three in the low wavelength region and two in the high wavelength region. In the low wavelength region, the peak at 0.7 µm differed from the desired design by 0.0253, at 0.7485 µm by 0.04587 and at 0.8152 µm by 0.0977; the closer to the rejection band the higher the difference. In the high wavelength region, the peak at 1.3 µm differed by 0.15 and at 1.197 µm by 0.1134; in this case, the further from the reflection band the higher the difference. All the minima outside the rejection band remained at the desired level. The transmittance curve was also less symmetrical than that of the desired curve by 2.75%. This result can be explained by the unequal number of peaks on either side of the rejection band and the position of the central wavelength with respect to the desired one. After 15 000 generations the merit value improved from 23.66 to 15.21.
The second optimisation was for an optical thickness starting population size of 150, on which the genetic algorithm was run for 15 000 generations. The spectral performance of this optimisation is depicted in Figure 2.

The rejection region had a bandwidth of 0.3216 µm, which was wider than the desired design by 11.552%. The FWHM was 0.2182 µm and equalled the one desired. The depth at the central wavelength was 0.11, which was 10% lower than desired and the central wavelength point shifted by 2% to 1 µm. The region outside the rejection band had four peaks, three of which were in the lower wavelength region and one was in the higher wavelength region. In the low wavelength region, the peak at 0.7 µm differed from the desired design by 0.082, at 0.803 µm by 0.123 and at 0.736 µm by 0.0739. In the high wavelength region, the peak at 1.227 µm differed from that which was desired by 0.0941. The uniformity in the decrease of the difference could not be seen in the low wavelength region as the last peak showed different behaviour. All the minima had the same level as that desired, except for the last minimum, which, at 0.7212 µm, was lower by 0.73% in the low wavelength region. The transmittance curve was less symmetrical to that of the desired curve by 4%. As with all other optimisation methods, optimising using the genetic algorithm decreased the number of layers, resulting in the layer thickness becoming unrealistically small and leading to the exclusion of the layer.1 The improvement in the merit value from 54.57 to 17.6 was seen after 15 000 generations.
Comparing the two optimisations it is clearly seen that the refractive index as a variable is a better performer than the optical thickness. The comparisons of the spectral performances inside and outside the rejection band show that the refractive index variable outperforms the optical thickness variable in every aspect. In studying the merit value, it was found that the refractive index variable converges faster, resulting in an improved final merit value. From this investigation it is possible to conclude that genetic algorithm optimisation, with respect to refractive index, produces a better result.
A possible reason why the refractive index variable outperforms the optical thickness variable could be that there is no precise method of converting the homogenous refractive index profile into its two material equivalents. The approximate way of converting the profile thus results in the deterioration of spectral performance. This has a direct effect on the optimisation convergence rate and the final merit value.
Design by genetic algorithm
A reflector with the same optical characteristics as was used for the optimisation process was designed by genetic algorithm in two ways, (1) with refractive index as a variable and (2) with optical thickness as a variable.
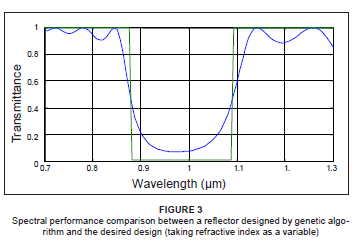
The genetic algorithm was run for 15 000 generations, taking refractive index as a variable. The rejection band in the spectral performance (shown in Figure 3) had a bandwidth of 0.2965 µm, which was wider than the desired design by 9.042%. The FWHM equalled that which was desired and the transmittance depth was 0.06908, which was 5.9% shallower than desired. The central wavelength shifted by 1.375% to the 0.99375 µm position. The region outside the rejection band had five peaks, three of which were in the low wavelength region and two in the high wavelength region. In the low wavelength region, the peak at 0.7 µm differed from the desired design by 0.0254, at 0.7485 µm by 0.0451 and at 0.8212 µm by 0.0901. In the high wavelength region, the peak at 1.197 µm differed by 0.1133 and by 0.1472 at 1.3 µm. In the low wavelength region, the peaks increased in size the closer they got to the rejection band, but the reverse occurred in the high wavelength region. All the minima stayed at the desired level. This spectrum was less symmetrical by 2.75% than the desired design. The merit value improved from 41.49 to 15.17 over the 15 000 generations.
The genetic algorithm was once again run for 15 000 generations, this time taking optical thickness as a variable. The rejection band in this spectral performance (shown in Figure 4) had a bandwidth of 0.2484 µm, which was wider than the desired design by 4.232%. The FWHM equalled that which was desired and the depth was >0.01. The reference wavelength shifted by 0.78% to a new position of 0.9878 µm. The region outside the rejection band had eight peaks, five of which occurred in the low wavelength region and three in the high wavelength region. In the low wavelength region, the peak at 0.7 µm differed from that which was desired by 0.0249, at 0.7303 µm by 0.0304, at 0.8091 µm by 0.044, at 0.7667 µm by 0.0298 and at 0.8515 µm by 0.0939. In the high wavelength region, the peak at 1.3 µm differed from the desired design by 0.0602, at 1.209 µm by 0.0406 and at 1.136 µm by 0.0839. A minimum occurred at 0.8636 µm in the low wavelength region, differing from the desired value by 0.0191, while, in the high wavelength region, the minimum at 1.112 µm differed by 0.01. The overall spectral performance was less symmetrical than the desired design by 1.56%. After 15 000 generations the merit value improved from 29 to 8.788.

The designs were then compared and it was found that the optical thickness variable demonstrated a far better performance than the refractive index variable. The spectral performance showed superiority both inside and outside the regions of rejection. The merit value converged faster when using optical thickness as a variable, resulting in an improved final value. However, this may not be the case every time because factors such as bandwidth can affect the result. For instance, it was seen that in the narrow band reflectors design, the refractive index variable outperformed the optical thickness variable. This investigation demonstrated that the choice of either the refractive index or optical thickness as a variable is dependent on the design specifications; hence the effect of the choice of variable is not distinct.
Comparing the performance of a genetic algorithm in the design and optimisation tasks provides important information about whether a genetic algorithm would be a good tool for optical thin film synthesis. Genetic algorithms used in design and optimisation applications perform excellently and, at the same time, the performance feature of a genetic algorithm in both applications shows some similarity. In both cases, however, the spectrum did not perform well in the high wavelength region when compared to the low wavelength region; the central wavelength shifts all favoured the high wavelength region. As a result, it was difficult to maintain symmetry within the transmission spectrum, especially in the high wavelength region. The FWHM also tended to keep the same value in both cases.
A genetic algorithm is easy to use for designing purposes, but it is not ideal to use it to optimise the results of other designs because other optimisation methods can provide a better result in much less time.1,3 The main difficulty in using a genetic algorithm as an optimisation tool is that its final result is directly dependent on the quality of the starting population and to create this quality is difficult. One significant drawback of using a genetic algorithm in both cases, however, is that a much longer generation time is needed to produce a quality result.
CONCLUSION
In optical thin film synthesis efficient design and optimisation methods are the basic elements needed for securing a refined design. A number of methods can be employed to execute this task. The ongoing research to find a better and refined method has always brought a great deal of improvement to the existing ones and has also often led to the development of entirely new methods.
The use of genetic algorithms is an emerging method that requires more research in order to be able to apply it efficiently in optical thin film synthesis. Hence our study was conducted to show the effect of the choice of variables when using a genetic algorithm either in designing or optimising optical thin films. We found that the refractive index variable provided a better result in the optimisation application than the optical thickness variable.
The creation of a quality starting population from other design methods (e.g. Fourier transform) is an enormous task. As a result, the use of a genetic algorithm may not be an ideal choice for the optimisation of optical thin film designs. Nevertheless, this study has shown that using a genetic algorithm is a very good and easy design method, of which the only significant drawback is the large generation time needed to produce the desired result. The final conclusion is that it is better to use a genetic algorithm in the design application than in the optimisation application in thin film synthesis.
ACKNOWLEDGEMENTS
We would like to thank the Department of Electrical and Electronic Engineering Science at the University of Johannesburg, the National Research Foundation of South Africa and the South African Technology and Human Resources for Industry Programme for funding the research conducted in this study.
REFERENCES
1. Dobrowolski J, Kemp R. Refinement of optical multilayer systems with different optimization procedures. Appl Opt. 1990;29:2876-2893. [ Links ]
2. Dobrowolski J. Computer design of optical coatings. Thin Solid Films. 1988;163:97-110. [ Links ]
3. Bloom A. Refining and optimization in multilayers. Appl Opt. 1981;20:66-73. [ Links ]
4. Fabricius H. Gradient-index filters: Designing filters with steep skirts, high reflection, and quintic matching layers. Appl Opt. 1992;31:5191-5196. [ Links ]
5. Dobrowolski J, Lowe D. Optical thin film synthesis program based on the use of Fourier transforms. Appl Opt. 1978;17:3039-3050. [ Links ]
6. Verly P, Dobrowolski J. Iterative correction process for optical thin film synthesis with Fourier transform method. Appl Opt. 1990;29:3672-3684. [ Links ]
7. Michelssen E, Ranjithan S, Mittra R. Optimal multilayer filter design using real coded genetic algorithm. IEE Proc Part J. 1992;139:413-420. [ Links ]
8. Man K, Tang K, Kwong S. Genetic algorithms: Concepts and applications. IEEE Trans Ind Electron. 1996;43:519-534. [ Links ]
9. Cusick T, Iezekiel S, Miles R. All-optical microwave filter design employing a genetic algorithm. IEEE Photonics Technol Lett. 1998;10:1156-1158. [ Links ]
10. Lai M, Jeng S. Compact microstrip dual-band bandpass filters design using genetic-algorithm techniques. IEEE Trans Microw Theory Tech. 2006;54:160-168. [ Links ]
11. Ejigu EK, Lacquet B. Design of reproducible polarized and non-polarized edge filters using genetic algorithm. J Opt. 2010;12(3):035401. [ Links ]
12. Swart P, Kotze A, Lacquet B. Effects of the nature of the starting population on the properties of rugate filters designed with genetic algorithm. J Lightwave Technol. 2000;18:853-859. [ Links ]
13. Fabricius H. Gradient-index filters: Conversion into a two index solution by taking into account dispersion. Appl Opt. 1992;31:5216-5220. [ Links ]
14. Houck C, Jones J, Kay M. The genetic algorithm optimization toolbox (genetic algorithmOT) for Matlab 5, NCSU-IE TR 95-09 [document on the Internet]. No date [cited 1996 July]. Available from: ftp://ftp.eos.ncsu.edu/pub/simul/genetic algorithmOT [ Links ]
15. Lidell HM. Computer-aided techniques for the design of multilayer filters. Bristol: Adam Hilger Ltd., 1981; p. 2-189. [ Links ]
 Correspondence to:
Correspondence to:
Efrem Ejigu
Postal address: PO Box 292030
Melville 2109, Johannesburg, South Africa
email: efremkz@gmail.com
Received: 11 Feb. 2010
Accepted: 23 Apr. 2010
Published: 05 July 2010
This article is available at: http://www.sajs.co.za














