Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.106 n.5-6 Pretoria May./Jun. 2010
RESEARCH LETTER
Competence of Science Foundation students in some simple strategies for problem solving
Mailoo Selvaratnam; Nkosana Mavuso
Science Foundation, North-West University, Mafikeng campus, South Africa
ABSTRACT
The competence of over 300 Science Foundation students in five important problem-solving strategies was studied at the North-West University over a period of three years. The study method adopted was the analysis of students' answers to carefully designed questions that tested whether they competently used the following strategies for problem solving: clarifying problems by presenting them clearly, identifying explicitly the principles and laws associated with the solutions, focusing sharply on the goal, using equations for deductions and calculations and proceeding step-by-step with the solution. The results showed that their competence in the use of intellectual strategies was very poor. This lack of competence could be expected to lead to lack of self-confidence and could also seriously handicap their learning throughout their courses. We suggest that greater emphasis should be placed, in all science courses, on the training of students in intellectual skills and strategies. Such training should be integrated with the teaching of subject content throughout the courses.
Keywords: intellectual strategies; problem solving; question testing strategies; thinking strategies; training of students
INTRODUCTION
Intellectual skills and strategies1,2,3,4,5,6,7 are the 'tools' for all our mental activities; competence in them is essential for effective learning and problem solving. A systematic study was done, over a period of three years (2006-2008), to test the competence of Science Foundation students at our university in some of the most important intellectual skills and strategies that are needed for successful problem solving in science. Details of this study were given in a paper previously published in this journal,8 which discussed students' competence in questions that tested intellectual skills. This paper will discuss their performance in questions used to test competence in intellectual strategies. Five intellectual strategies were tested:
• clarifying problems initially by presenting them clearly
• identifying the principles and laws associated with the solutions
• focusing sharply on the goal and formulating a strategy for reaching that goal
• using equations, whenever possible, for deductions and calculations
• proceeding step-by-step in order to formulate a solution.
The usefulness of these strategies for successful problem solving will be discussed, along with the analysis of students' answers, in the Results and Discussion section of this paper. Some of these strategies are also useful for solving problems encountered in daily life.
SUBJECTS OF THE STUDY
The students tested were Science Foundation students at the North-West University. Science Foundation students do not have the minimum qualifications needed to enter science courses at universities and the main objective of the Science Foundation programme is to rectify this limitation. The majority of the students were from under-resourced rural schools in the North-West Province and from 'township' schools in other provinces. Most of them had a matriculation pass, at the standard grade, in mathematics and one or two science subjects and had an M-score of 4. The total number of students tested was 313: 110 students in 2006, 99 students in 2007 and 104 students in 2008.
METHODS
The study method used was the analysis of students' answers to carefully designed questions. The study involved diagnostic testing of students to identify the areas in which they were having difficulties in processing the appropriate information. The criteria used to design the test questions and the method of question administration were detailed in the previous paper.8
A representative sample of the questions used in this study is given in Table 1. These questions have been classified in the table into five types, based on the type of strategy tested.
RESULTS AND DISCUSSION
Table 1 comprises (from left to right) a sampling of the questions used in the study, the number of students tested for each question and the percentage of students who answered each question correctly. The number of students varied from question to question because some questions were used in the test for one year only and others for two years; the specific test year is indicated in parenthesis after each number. The results showed that students' competence in most of the intellectual strategies tested was very poor.
Clarifying problems initially so as to aid solution
Questions 1-5 tested whether students used the important strategy of first clarifying problems (e.g. by drawing a diagram that correlates all the relevant data given) before attempting their solutions.
Question 1 is easy to answer if the data given are first correlated together in a diagram. The required answer may then be read easily from the diagram below:
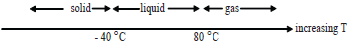
The diagram, itself, provides the answers: no reasoning is required. From the diagram it is easy to see that the substance will be a solid at -50 ºC, a liquid at 50 ºC and a gas at 90 ºC. About 40% of the students tested, however, were unable to answer this question correctly. Most of these students did not attempt to correlate the data given (e.g. by drawing a diagram). They either did not recognise the importance of doing this to aid the solution or were unable to correlate the given information.
Question 2 was very poorly answered. Part (a) of this question merely tests the ability to represent, in a correlated manner, the information given as a diagram (see figure below).
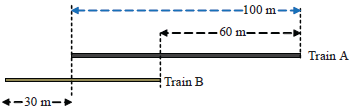
More than 80% of the students tested, however, were unable to do this. This problem does not have conceptual difficulties. It only tests the ability to identify clearly the information given and process it step-by-step. More than 20% of the students did not even attempt to answer the question: this suggests avoidance of mental effort and perhaps a lack of self-confidence.
Question 3, like Question 2, is a simple non-science question, but about 35% of the students tested could not solve it. Again, the solution is easy if one proceeds step-by-step and tabulates the steps in the solution. The answer is: A, 4 litres; B, 6 litres; C, 7 litres; D, 15 litres. Tabulation is often a useful strategy for solving some types of problems in science, for example, problems involving balanced equations for reactions.
Questions 4 and 5 are similar. The noteworthy difference between them is that in Question 5, unlike in Question 4, one is asked first to represent the given information as a diagram. Comparison of performance in Questions 4 and 5 should reveal whether students' difficulties are due to, (1) their failure to recognise the necessity for first correlating the given information as a diagram or (2) their inability to accomplish this. The results (Table 1) showed that 65% of the students tested were able to represent the information given in the problem statement on a line and then answer Question 5 correctly. In contrast, only 46% solved Question 4. This suggests that the difficulties of some students in solving Question 4 may, again, result from their failure to recognise the usefulness of initially correlating the given information as a diagram before attempting its solution.
Identifying the principles and laws associated with the solutions
Questions 6-8 tested whether the students recognised that deductions and conclusions must always be based on principles and laws. Question 6 deals with mass. Since this is a basic physical quantity, it is independent of any other physical quantity, such as length, time or temperature. Thus, in order to answer this question correctly, students needed to recognise that mass will not depend on pressure or temperature. About 85% of the students tested, however, thought that mass changes when temperature is changed; most of them thought that mass will be doubled when temperature is doubled and halved when pressure is doubled.
Question 7 was also very poorly answered. About 90% of the students thought that the volume of a liquid will be doubled when temperature is doubled, despite the fact that this contradicts familiar experience (e.g. we know that the volume of water increases only slightly when it is heated). Students' answers to Questions 6, 7 and 9 (and also their answers to other questions not given here) suggest that many of them implicitly assume, without any justification, that when the value of some physical quantity is doubled the value of another quantity will also be doubled.
About 85% of students answered Question 8(a) incorrectly; most students thought that when 2000 cm3 of liquid 'A' is mixed with 2000 cm3 of liquid 'B', the final volume will be 4000 cm3. This is incorrect because volume, unlike mass, is not an additive property. Masses can be added together, as a consequence of the law of conservation of mass, which states that mass cannot be created or destroyed. But this law cannot be applied to volume and thus, the final volume cannot be calculated from the data given in this question.
Students' answers to Questions 6-8 reveal that the majority do not recognise that deductions and conclusions must always be based on principles and laws. Lack of recognition of this important requirement often leads to errors and failures in problem solving.
Focusing sharply on the goal
Questions 9-11 were designed to test whether students begin to solve a problem by identifying and focusing on the goal4 (e.g. by identifying and focusing on the physical quantity that has to be calculated). This is a very important strategy because it would simplify problem solving and help avoid errors.
In Question 9, the goal is the calculation of the mole fraction (xA), for which the defining equation (xA = nA/ntotal) was given in the problem statement. This equation shows that xA depends only on nA (moles of substance A) and ntotal (total moles of all substances present). Therefore, xA cannot be affected by any other quantity unless it changes nA or ntotal. Owing to the fact that nA and ntotal are basic physical quantities that are not affected by any other quantity, xA will not change if temperature or pressure is changed. Although the solution to this question is easy, student performance was very poor, with only about 5% of them recognising that the mole fraction does not depend on temperature or pressure. Most students thought that mole fraction will be doubled when temperature or pressure is doubled. The error of these students is probably a result of their failure to focus on the defining equation for xA to deduce the answer.
Question 10, like Question 9, is easy to solve if one starts the solution by focusing on the defining equation for the required quantity (density), which is density = mass/volume. Since mass (3.00 g) and volume (1.00 dm3) are given in the data, density = 3.00 g/1.00 dm3. If one begins the solution of the problem with the defining equation and uses it to do the required calculation, then all the data and information given that are irrelevant will not cause any confusion. Despite its simplicity, about 55% of the students tested were unable to solve this problem correctly. Analysis of students' answer scripts revealed that most of the unsuccessful students tried to use the given equation for the dissociation of PCl5 (an irrelevant equation) to do the calculation. Some of them tried to use this equation to calculate the mass of PCl3 formed, while others tried to calculate the mass of undissociated PCl5. This problem (albeit a more difficult version) has been tested on more than 500 chemistry students in Sri Lanka, the United States of America and the United Kingdom, with more than 75% of these respondents having difficulty.9
Question 11, which also primarily tests whether one starts the solution by focusing on the defining equation for the required quantity, is more difficult to solve than Questions 9 and 10. This is because the solution also requires the distinction between two related quantities: volume of solvent and volume of solution. Because the total volume of ethanol and water will evidently be greater than the volume of water (which is 1.00 dm3), the concentration c, in the equation c = n/V, will be less than 1.0 mol/dm3 (because n = 1.00 mol and V is greater than 1.00 dm3). The results indicated that 85% of the students did not solve this problem correctly; most students thought that V = 1.00 dm3 and therefore that c = 1.00 mol/dm3.
It was hypothesised above that the primary reason for students' poor performance in Questions 9, 10 and 11 can be associated with their failure to start the solutions by identifying the goal and focusing sharply on it. Previous research4,9,10 also supports this hypothesis and, therefore, it is our opinion that this is one of the most significant reasons for students' failures in problem solving.
Use of equations for calculations and deductions
Questions 12-15 tested whether the students used equations,10,11 and not verbal reasoning, for calculations and deductions. Often students use verbal reasoning (i.e. reasoning using statements) for some types of deductions and calculations, even though equations could be used. Verbal reasoning, however, is cumbersome, more difficult and more error-prone and it may be advisable to avoid it whenever possible.
Question 12 is straightforward to solve if one uses the defining equation for density (density = mass/volume) for deducing the answer. This equation shows that density depends only on mass and volume. It will not depend on any other quantity unless that quantity affects mass or volume. In the problem considered, mass and volume are constant and therefore density will not change, when temperature is changed, from its initial value of 2.0 × 10-3 g/cm3. Although the solution is easy, about 70% of the students tested had difficulty in answering the question. Their difficulty was probably because they did not analyse the defining equation for density to deduce the answer.
Question 13 is not difficult to solve if the law of conservation of mass, which was given as a statement in the question, is first transformed into an equation that is then used for the calculations. The statement given for the law of conservation of mass may be transformed into the general equation mtotal (before reaction) = mtotal (after reaction). For the reaction considered in Question 13, the total mass before chemical reaction is 0.50 g. After the reaction at 50 ºC, the substances present are N2O4 and NO2 and therefore mtotal (after reaction) = mN2O4 (at 50 ºC) + mNO2 (at 50 ºC). Application of the general equation written above to the problem considered will therefore give
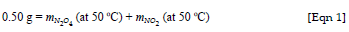
The use of this equation to do the required calculations is simple and shows that mN2O4 (at 50 ºC) = 0.30 g and mtotal (at 50 ºC) = 0.50 g. Students' performance in this question (Table 1) was very poor: about 90% (average performance in the two parts over 2 years) of the students tested were unable to answer it. The main reason for their difficulties was probably their use of verbal reasoning.
Questions 14 and 15 were also poorly answered. Here too, as in Question 13, students' difficulties were probably a result of their attempts to solve the problems through verbal reasoning. The solutions would be easier, in our view, if the relevant information in the problem statements are transformed first into equations and the equations are then used for the calculations. The equation relating the selling price (S), cost price (C) and profit (P) (see Question 14) is

and the two equations relating the two quantities x and y (see Question 15) are

Proceeding step-by-step
Questions 16 and 17 tested whether the students proceeded with the solution of a problem in a step-by-step manner, concentrating on just one step at a time, without being distracted by the other steps. This is an important strategy for successful problem solving because it allows the complete problem to be broken down into simpler problems that are easier to solve.
Question 16 involves the use of a simple equation (t = k/N) to calculate the time t needed by three men (i.e. N = 3) to paint the walls of a house, if two men need 9 hours. Though this problem is simple and familiar, over 80% of students were unable to solve it. This suggests incompetence in step-by-step reasoning. The given equation has to be applied twice, using step-by-step reasoning, to solve this problem. The equation t = k/N shows that to calculate the time t needed by three men (i.e. N = 3) to paint the walls of a house, the value of k must be known. Because this is not given, it must first be calculated and this can be done by applying the equation t = k/N to the given data (t = 9 hours when N = 2 men). Then, using this value of k, the time needed by three men to paint the walls of the house can be calculated as 6 hours.
Question 17 also tested whether a step-by-step method was used to calculate the average speed. Over 90% of the students were unable to do this calculation, with most of them calculating the average speed incorrectly, by adding together the two speeds of the car (80 km/h and 100 km/h) and then dividing that either by two or by the total time taken for travel.
Further investigation of students' answers for Questions 16 and 17 revealed that the main reason for their poor performances in these two questions was their attempts to do the calculation in one step.
CONCLUSION
In this study, in which the main objective was to test, using carefully designed questions, the competence of Science Foundation students at the North-West University in five important intellectual strategies, we showed that most of the students tested were not competent in this regard.
There are two aspects to the difficulties associated with the use of strategies. These are, (1) the lack of recognition of the usefulness of the strategy and (2) inability to use the strategy (which will need competence in some intellectual skills). The students tested had difficulties with both these aspects. The results of this study essentially agree with those obtained by Drummond12, although Drummond's study focused on first year university students and used questions that were more difficult than the questions in this study.
Lack of competence in intellectual skills and strategies could be expected to lead to a lack of self-confidence and avoidance of mental effort, which would seriously handicap the ability of students to learn throughout their courses. This lack of competence may be the reason for many students memorising standard 'recipes' and procedures and trying to use them for problem solving. When confronted with unfamiliar problems, such as those given in this test paper, most students do not seem to know where to start and how to proceed with obtaining the solutions. They then manipulate the given data and the equations with which they are familiar, without much understanding.
Emphasis in most educational courses in South Africa (which may also be true for many other countries) is predominantly on subject content knowledge. The curriculum, for example, is generally stated only in terms of knowledge that has to be learned and insufficient emphasis is placed on the explicit training of students in intellectual skills and strategies. This approach is undesirable because the development of students' intellectual abilities should be a primary objective of all science courses.3 We strongly suggest that greater emphasis should be placed on the systematic training of students in intellectual skills and strategies. Such training should be integrated with the teaching of subject content throughout the courses.
REFERENCES
1. Marzano RJ, Brandt RS, Hughes CS, et al. Dimensions of thinking: A framework for curriculum instruction. Alexandria: Association for Supervision and Curriculum Development; 1988. [ Links ]
2. Selvaratnam M, Frazer MJ. Problem solving in chemistry. London: Heinemann Educational Publishers; 1982. [ Links ]
3. White RT. Learning science. Oxford: Basil Blackwell; 1988. [ Links ]
4. Selvaratnam M, Mazibuko B. Importance of focusing sharply on the goal for successful problem solving. S Afr J Chem. 1998;51:42-46. [ Links ]
5. Cook E, Cook RL. Cross proportions: A conceptual method for developing quantitative problem-solving skills. J Chem Educ. 2005;82:1187-1189. [ Links ]
6. Gagne RM. The conditions of learning. New York: Holt, Rinehart and Winston; 1977. [ Links ]
7. Selvaratnam M, Canagaratna SG. Using problem-solution maps to improve students' problem solving skills. J Chem Educ. 2008;85:381-385. [ Links ]
8. Selvaratnam M, Mavuso N. Competence of Science Foundation students in basic intellectual skills. S Afr J Sci. 2010;106(1/2):70-75. [ Links ]
9. Selvaratnam M, Frazer MJ. Problem solving in chemistry. London: Heinemann Educational Publishers, 1982; p. 2. [ Links ]
10. Selvaratnam M. Students' difficulties with problem solving. Educ Chem. 1983;20:126-131. [ Links ]
11. Selvaratnam M. A guided approach to learning chemistry. Cape Town: Juta & Co, 1998; p. 17-22. [ Links ]
12. Drummond HP. Students' competence in the intellectual skills and strategies needed for learning South African matriculation chemistry effectively. PhD thesis, North-West University, Mafikeng; 2003. [ Links ]
 Correspondence to:
Correspondence to:
Nkosana Mavuso
Postal address:
Science Foundation, North-West University
Private Bag X2046, Mmabatho
2735, South Africa
email: Nkosana.Mavuso@nwu.ac.za
Received: 10 July 2009
Accepted: 10 Mar. 2010
Published: 31 May 2010
This article is available at: http://www.sajs.co.za














