Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.106 n.3-4 Pretoria Mar./Apr. 2010
RESEARCH ARTICLE
Channel and delay estimation for base-station-based cooperative communications in frequency flat-fading channels
Hongjun Xu; Laneil Padayachee
School of Electrical, Electronic and Computer Engineering, University of KwaZulu-Natal - Howard College campus, South Africa
ABSTRACT
Base-station-based cooperative communication is an asynchronous cooperative communication system. The challenge therein is to estimate the relative delay between the transmitters in the system. A channel and delay estimation algorithm based on the distributed Alamouti scheme has been previously discussed for the asynchronous cooperative system. The algorithm only makes accommodation for positive delay, that is, when data from Transmitter one always arrives at the receiver before data from Transmitter two. In reality, the data from Transmitter one does not always arrive at the receiver before data from Transmitter two in the asynchronous cooperative system, because of the constantly changing mobile environment in the system. This paper extends the algorithm to accommodate both positive and negative delays, which is when the data from Transmitter one arrives at the receiver before or after data from Transmitter two, in a Rayleigh block flat-fading channel. Simulation results show that the Cramér-Rao lower bound for channel and delay estimation is achieved for different delay values. The symbol error rate performance is also achievable compared to the channel and the delay is known at the receiver.
Keywords: asynchronous cooperative communication; channel estimation; cyclic prefix; distributed space-time coding; pilot symbol design
I. INTRODUCTION
Cooperative diversity is a relatively new transmission scheme that combines the ideas of relays and multiple antennas, while avoiding the size limitations of a single mobile node. It provides spatial diversity by allowing multiple nodes, each with a single antenna (it is possible to increase the number of antennas), to work together to form a virtual multiple-input-multiple-output (MIMO) system. Sendonaris et al.1,2 have shown that even with a noisy inter-user channel, cooperative communication still leads to improved performance, and is generally a more robust system. One real MIMO system is the space-time block code (STBC) system, which achieves both space and time diversity. If both STBC and cooperative diversity are incorporated together, a distributed STBC system is formed.3,4
In this paper, we focus on cooperative communication using the Alamouti scheme,5 which is a special-case, full-rate orthogonal STBC with two transmit antennas and one receive antenna. A typical example of the system is a base-station-based cooperative communication in macrocell downlink networks, which is proposed by Skjevling et al.6 In the base-station-based cooperation system, all base stations are connected via a very fast-wired local area network and are setup to transmit data to one mobile user. Skjevling et al.6 discussed a precoded distributed STBC synchronous cooperative diversity system. But in reality this scenario is unlikely. The challenge therein is to estimate the relative delay between the transmitters in the system. This problem has been addressed, which resulted in a channel and delay estimation algorithm that achieved the lower Cramér-Rao bound (CRB).7 Tourki and Deneire provided a simple maximum likelihood channel and delay estimation algorithm, but this system was only derived for positive delays, that is, when Transmitter one's data always arrives at the receiver before Transmitter two's data.7
The main motivation behind this paper is to extend the scheme in Tourki and Deneire7 to accommodate negative delays (i.e. when Transmitter two's data arrives at the receiver before Transmitter one's data). This extension is significant, for example, in the case of a macrocell, as considered in this paper. Specifically, the macrocell considered here consists of two base stations transmitting the same data to one node. Since the node is mobile, it could be closer to either base station at any given time, and it cannot be arbitrarily assumed that the first signal it receives is from base station one, as the Alamouti's scheme5 strictly dictates the role of each of the two transmitters in the transmission scheme. By extending the delay estimation search to negative delays, the receiver can determine which transmitter's data arrived first, and hence properly decode the received signals.
This paper is structured as follows: in Section II, the system model of Tourki and Deneire7 is extended to accommodate negative delays, in Section III the channel and delay estimation algorithm for both positive and negative delays is derived, in Section IV the detection scheme for a single receiver is shown, in Section V the symbol error probability is discussed, in Section VI the simulation results are presented and, finally, in Section VII the conclusions are drawn.
II. SYSTEM MODEL
The system model consists of two base stations (BS1 and BS2) transmitting data to one mobile node, each with a single transceiver.7 The channel gains from BS1 and BS2 to the mobile node are h1 and h2 , respectively, where h1 and h2 are assumed to be the complex scalar channel parameters. It is assumed that both base stations have knowledge of both pilot sequences d1 and d2. In reality, this can be achieved via either a wired, high-speed connection such as Ethernet, or a wireless transmission of the data between two base stations preceding the transmission scheme presented here.
The data sequences to be transmitted are replicated in space and timeaccording to the time-reversed block form of the Alamouti's scheme,5 allowing the mobile node to combine and decode the two received signals, using a simple linear technique while enjoying the benefits of spatial diversity.
The data transmission model is shown in Figure 1. To begin with, the data set to be transmitted is parsed into two blocks of N symbols each, dn and dn+1, where n is the block number. Training symbols d1 and d2, each of length L, are then added at the end of dn and dn+1, respectively, to form two (N + L) x 1 vectors. To insert a cyclic prefix of training symbols between any two successive blocks, these vectors are pre-multiplied by a precoding matrix Fp. Multiplying the vectors by Fp results in two (N + 2L) x 1 blocks, sn and sn+1.
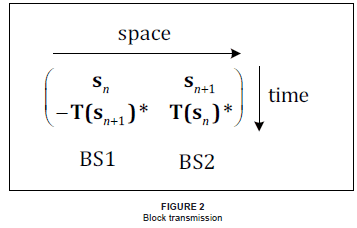
The blocks are then transmitted according to the time-reversed block form of the Alamouti's scheme shown in Figure 2. In Figure 2, (.)* indicates the complex conjugate operator.
The precoding matrix Fpand time-reversal matrix T 7 are given by
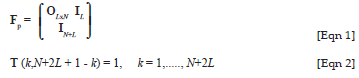
where OLxN is a (L x N) matrix of zeros, IL and IN+L are identity matrices of dimensions (L x L) and (N + L) x (N + L), respectively.
By defining τ = τ2 - τ1 as the difference between the arrival time of the two signals, where τ1 and τ2 are the arrival times of the first (BS1) and second (BS2) signal respectively, the received signal r can then be defined as7

where
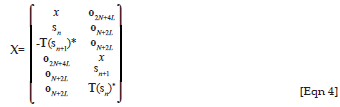
and

In [Eqn 3] to [Eqn 5], r is a symbol vector of length (2N + 4L); τ  [-(L-1), L-1] is the relative delay between the two received signals; hi, i = 1, 2, are the zero mean complex scalar channel parameters. They are also assumed to be Rayleigh block flat-fading, that is, the amplitude of the fading envelope follows a Rayleigh distribution which stays constant for the duration of each frame, but varies independently from frame to frame. In [Eqn 3], b is assumed to be zero mean complex additive white Gaussian noise (AWGN), with each entry having a variance of N0/2 per dimension, while X is the data matrix where x denotes symbols from the previous frame which are treated as 'don't-cares'. The matrix A(τ), denotes the delay matrix.
[-(L-1), L-1] is the relative delay between the two received signals; hi, i = 1, 2, are the zero mean complex scalar channel parameters. They are also assumed to be Rayleigh block flat-fading, that is, the amplitude of the fading envelope follows a Rayleigh distribution which stays constant for the duration of each frame, but varies independently from frame to frame. In [Eqn 3], b is assumed to be zero mean complex additive white Gaussian noise (AWGN), with each entry having a variance of N0/2 per dimension, while X is the data matrix where x denotes symbols from the previous frame which are treated as 'don't-cares'. The matrix A(τ), denotes the delay matrix.
For positive delay A(τ) is given by
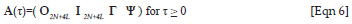
where
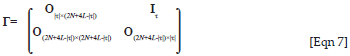
and
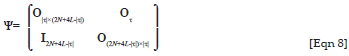
where |·| is the absolute value operator.
It is worthwhile to note that for the synchronous case, 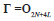 and
and 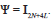 .
.
To extend the received signal model to accommodate negative delays, one needs only to modify [Eqn 6]. To understand this extension, one first needs to understand how [Eqn 6] accounts for the asynchronicity of the system. Figure 3 shows the illustration of A(τ) for τ > 0.
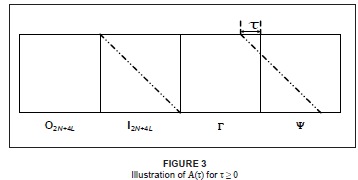
In Figure 3, the dashed-dotted lines represent ones and blank spaces represent zeros in the corresponding matrices.
When A(τ) is multiplied by the data matrix X, for τ > 0 it can be seen that the received signal from BS1 will just be s1[n], but from BS2, the delayed τ symbols from the previous frame [s2(n-1)] are received first and the last τ symbols of s2[n] will be received in the next frame.
For negative delays, only the symbols from BS1 will be delayed, and hence the resulting equation for A(τ) is
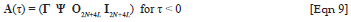
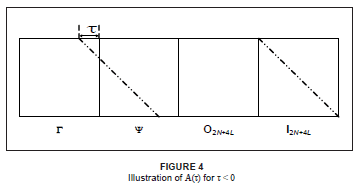
Figure 4 shows the illustration of A(τ) for τ < 0. Once again, the dashed-dotted lines represent ones, and blank spaces represent zeros in the corresponding matrices.
III. CHANNEL AND DELAY ESTIMATION ALGORITHM
A maximum likelihood (ML) estimator used by Tourki and Deneire7 and Sirbu8 is also used for the channel and delay estimation in this section. Firstly we summarise the estimation algorithm of Tourki and Deneire7 for τ > 0, and then use the same approach to derive the estimation algorithm for τ < 0.
Let ts1 and ts2 be defined as

where Ts is a time-reversal matrix of size L (i.e. Ts is basically a small version of the matrix T).
The section of the received signal where the pilot symbols from each transmitter overlap are defined as S(τ) = [ss1(τ) ss2(τ)]. For convenience, 'L1:L2' is defined as a sequence from index L1 to L2.
Figure 5 shows S(τ) for τ > 0, where ss1 and ss2 are defined as

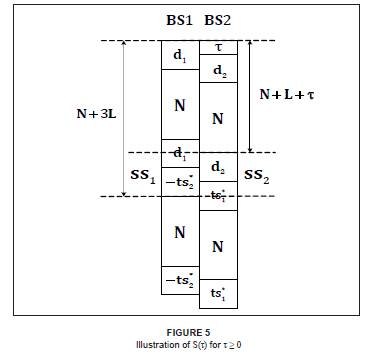
and

Figure 6 shows S(τ) for τ < 0. From Figure 6, it is observed that the symbols from BS1 are shifted.
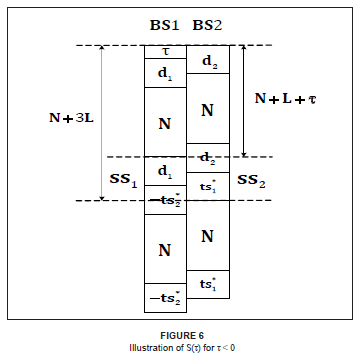
The modified equations for ss1 and ss2 for τ < 0 are given by

From Figures 5 and 6, one can define z(τ) as z(τ) = S(τ)h = r(N + L + |τ| + 1: N + 3L). It then follows that7

where [.]# represents the pseudo-inverse operator and  is the linear least squares estimate of h for a given value of τ.
is the linear least squares estimate of h for a given value of τ.
Since delay search space has been extended to accommodate negative delay values, the ML estimator used by Tourki and Deneire7 and Sirbu8 has to be modified to

and

where  is the final estimate of h based on the delay estimate
is the final estimate of h based on the delay estimate 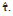
The minimum square error (MSE) of the channel estimation is given by

where E[.] is the expectation operator and H represents the conjugate and transpose operation.
IV. DETECTION SCHEME
The data symbols are extracted and decoded as follows:
While ignoring the noise terms, define ra and rb as7
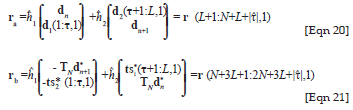
where TN is a time-reversal matrix of size N.
For a clearer understanding, ra and rb are illustrated in Figures 7 and 8.
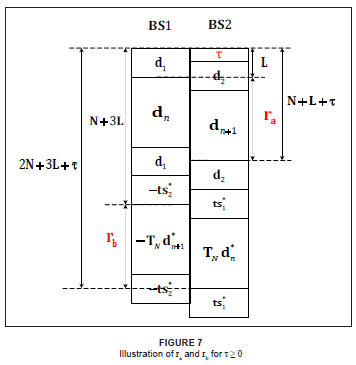
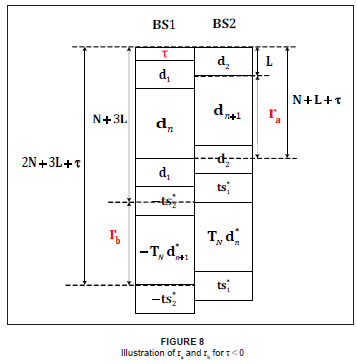
A block form of the decoding scheme has been derived here, and uses the same orthogonal system properties as the scheme in Tourki and Deneire7. As will be shown, the following block form also allows for a simple modification to accommodate negative delays.
Define rw, rx and rn as
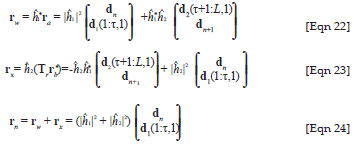
where Tr is a square time-reversal matrix of size N + τ, and ra and rb are defined in [Eqn 20] and [Eqn 21], respectively.
The estimate of 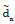 for τ > 0 is given by
for τ > 0 is given by

Define ry, rz and rn+1 as
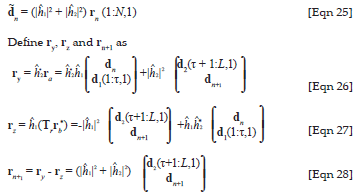
Then the estimate of 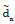 +1 for τ > 0 is given by
+1 for τ > 0 is given by
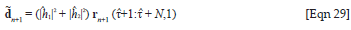
Using a similar approach one can obtain the estimate of dn and dn+1for τ < 0 by
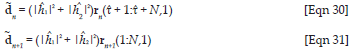
V. SYMBOL ERROR RATE
The symbol error rate (SER) of orthogonal STBC over Rayleigh block flat-fading channels can be evaluated using the well-known approach of averaging the conditional SE R, P(E|γ), over the probability density function, pγ(γ), of the instantaneous signal-to-noise ratio (SNR) per symbol, γ, as shown below

The analysis done by Shin and Hong Lee9 yields the closed form SER of STBC for M-PSK signals transmitted over a Rayleigh block flat-fading channels as
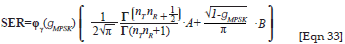
where
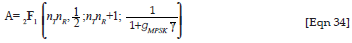
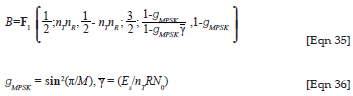
with Es being the symbol energy and R being the transmission rate, the numbers nT and nR are the numbers of transmit and receive antennas, respectively, 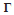 (.) represents the gamma function, 2F1 and F2 represent the Gauss and Appell hypergeometric functions respectively and φ is the moment generating function for the instantaneous SNR given by
(.) represents the gamma function, 2F1 and F2 represent the Gauss and Appell hypergeometric functions respectively and φ is the moment generating function for the instantaneous SNR given by

VI. SIMULATION RESULTS
In our simulations, each block contains 140 symbols of which 112 are used for data and L = 14 for the pilot sequence. When choosing the pilot sequence length, there is a trade-off between estimation performance and bandwidth efficiency. With this in mind, a sequence length of 14 was chosen as a reasonable balance between the two. The 4-PSK modulation was used, and the channel and noise parameters used were as described from [Eqn 3]. The channels were assumed to be unknown and hence needed to be estimated. Unless otherwise stated, the delay was assumed to remain constant over each frame, but was allowed to vary randomly from frame to frame. The delays were uniformly distributed between -(L-1) and (L-1). The SNR values that were used refer to the ratio between symbol and noise energy. The single-input-single-output (SISO) equaliser used was a minimum mean square error (MMSE) equaliser.
Channel estimation performance
Channel and delay estimation was normally implemented using a training sequence or pilot sequence. Tourki and Deneire7 did not discuss the method to design the pilot sequence. To estimate channel and delay, it is not merely enough to simply transmit a known set of symbols as pilot sequences. These sequences have to be carefully designed in order to achieve the best channel estimation performance possible. The design of the pilot sequence in frequency flat-fading channels for asynchronous cooperative communication systems has been discussed by Padayachee10,11. To derive optimal pilot sequences, the base station has to have information about the channel delay. In Padayachee10,11, a packet transmit scheme was proposed to enable the base stations to use an estimate of the delay to select the corresponding optimal pilot sequences for that specific delay.
The scheme can be divided into three phases. In the first phase, the base stations transmit x pilot frames consisting of pilot symbols only. The mobile receiver then uses these frames to obtain an average estimate of the channel delay, and then transmits the estimated delay back to the base stations via the feedback channel in phase two. In phase three, the base stations use this delay estimate to select the corresponding optimal pilot sequences for channel estimation, to be used in the next y normal frames consisting of data and pilot symbols. It is assumed that the delay remains constant over each round of the above three phases, but is allowed to vary from round to round.
In our simulations, we also use the two transmit schemes. Figure 9 shows the MSE performance of the channel estimation. It has the following plots:
• MSE of the channel estimation when the channel and delay are unknown.
• MSE of the channel estimation when the channel and delay are unknown and where the packet scheme is used. After every 200 data frames, five pilot symbol frames are sent at an SNR of 10 dB.
• CRB for channel estimation.
The CRB serves as a fundamental lower bound on the performance of any unbiased estimator. The CRB for channel estimation as derived by Berriche et al.12 is given by

where tr(.) represents the trace operator. It is important to note, however, that this bound was derived assuming that the delay was a known parameter, therefore it is only used here in order to obtain a tractable comparison.
It can be observed from Figure 9 that, for low SNRs, the channel estimation of the normal scheme significantly differs from the CRB, due to the relatively high error rate of the delay estimation. However, using the packet scheme, which has a relatively low error rate, the channel estimation performance practically achieves the CRB. This is because feedback is used in the packet transmit scheme to choose an optimal pilot sequence.
SER performance
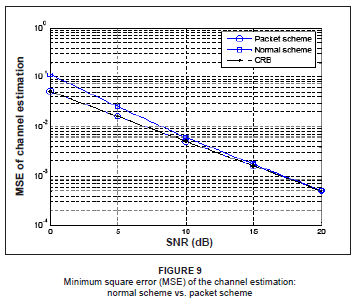
The SER derivation [Eqn 33] was done assuming that the channel and delay were known parameters, as obtaining a closed form expression of the SER would otherwise prove rather complex. This assumption was made in order to obtain a tractable comparison, and its result is plotted in Figure 10 as the 'ideal'.
From Figure 10, it can be observed that at low SNRs, the normal scheme performance is between 1 dB and 2 dB worse than the 'ideal', whereas the packet scheme is approximately 0.5 dB off the 'ideal'. This performance demonstrates that if the packet scheme is used, relaxing the known channel and delay assumption only results in a mere 0.5 dB difference. Also, if the channel is assumed to be known, the delay estimation exhibits very low error rate and the SER performance achieves the 'ideal', demonstrating that the channel estimation dominates the system performance.
VII. CONCLUSION
In this paper, the scheme proposed by Tourki and Deneire7 was extended to accommodate negative delays in base-station-based cooperative communication systems. The various concepts and modifications were explained in detail. A block form of the decoding scheme was also presented, which allowed for a simple modification to accommodate negative delays. Both the normal scheme and the packet scheme were simulated. It was shown via the simulations that the packet scheme outperformed the normal scheme by achieving the CRB for channel estimation. As far as the SER is concerned, the packet scheme demonstrated that performance gains were achievable at minimal expense in bandwidth efficiency. The only limitation for the packet scheme is that the delay remains constant over the three phases. Possible future work would be to extend the scheme presented in this paper into frequency-selective fading channels.
REFERENCES
1. Sendonaris A, Erkip E, Aazhang B. User cooperation diversity. Part I: System description. IEEE Trans Commun. 2003;51(11):1927-1938. [ Links ]
2. Sendonaris A, Erkip E, Aazhang B. User cooperation diversity. Part II: Implementation aspects and performance analysis. IEEE Trans Commun. 2003;51(11):1939-1948. [ Links ]
3. Laneman JN, Wornell GW. Distributed space-time coded protocols for exploiting cooperative diversity in wireless networks. IEEE Trans Inf Theory. 2003;49(10):2415-2425. [ Links ]
4. Li X. Space-time coded multi-transmission among distributed transmitters without perfect synchronisation. IEEE Signal Process Lett.2004;11(12):948-951. [ Links ]
5. Alamouti SM. A simple transmit diversity technique for wireless communications. IEEE J Sel Areas Commun.1998;16(8):1451-1458. [ Links ]
6. Skjevling H, Gesbert D, Hjørungnes A. Precoded distributed space-time block codes in cooperative diversity-based downlink. IEEE Trans Wireless Commun.2007;6(12):4209-4214. [ Links ]
7. Tourki K, Deneire L. Channel and delay estimation algorithm for asynchronous cooperative diversity. Wireless Pers Commun.2006;37:361-369. [ Links ]
8. Sirbu M. Channel and delay estimation algorithms for wireless communication systems. PhD thesis, Helsinki University of Technology, Helsinki; 2003. [ Links ]
9. Shin H, Hong Lee J. Exact symbol error probability of orthogonal space-time block codes. Paper presented at: IEEE Globecom 2002. Proceedings of IEEE Globecom conference; 2002 Nov 17-21; Taipei, Taiwan. New York: IEEE Communications Society; 2002, p. 1197-1201. [ Links ]
10. Padayachee L. A channel and delay estimation algorithm for asynchronous cooperative diversity with pilot symbol design. Paper presented at: SATNAC 2008. Proceedings of Southern African Telecommunication Networks and Applications Conference; 2008 Sep 7-10; Wild Coast Sun, Eastern Cape, South Africa. Pretoria: Telkom; 2008. [ Links ]
11. Padayachee L. Asynchronous cooperative communication with channel and delay estimation. MSc thesis, University of KwaZulu-Natal, Howard College campus, Durban; 2009. [ Links ]
12. Berriche L, Abed-Meraim K, Belfiore JC. Cramér-Rao bounds for MIMO Channel Estimation. Paper presented at: IEEE International Conference on Acoustics, Speech, and Signal Processing 2004. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing; 2004 May 17-21; Montreal, Canada. New York: IEEE Signal Processing Society; 2004, p. 397-400. [ Links ]
 Correspondence to:
Correspondence to:
Hongjun Xu
Postal address:
School of Electrical, Electronic and Computer Engineering, King George V Avenue
Durban, 4041, South Africa
email: xuh@ukzn.ac.za
Received: 20 Oct. 2009
Accepted: 11 Jan. 2010
Published: 23 Apr. 2010
This article is available at: http://www.sajs.co.za














