Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.105 n.11-12 Pretoria Nov./Dec. 2009
REVIEW ARTICLES
Experimental measurement and computational fluid dynamics simulation of mixing in a stirred tank: a review
A. OchiengI, *; M. OnyangoII; K. KiriamitiIII
IDepartment of Chemical Engineering, Vaal University of Technology, Private Bag X021, Vanderbijlpark 1900, South Africa
IIDepartment of Chemical and Metallurgical Engineering, Tshwane University of Technology, Private Bag X680, Pretoria 0001, South Africa
IIIDepartment of Chemical and Process Engineering, Moi University, P.O. Box 3900, Eldoret, Kenya
ABSTRACT
Stirred tanks are typically used in many reactions. The quality of mixing generated by the impellers can be determined using either experimental and simulation methods, or both methods. The experimental techniques have evolved from traditional approaches, such as the application of hot-wire anemometry, to more modern ones like laser Doppler velocimetry (LDV). Similarly, computational fluid dynamics (CFD) simulation techniques have attracted a lot of attention in recent years in the study of the hydrodynamics in stirred tanks, compared to the empirical modelling approach. Studies have shown that the LDV technique can provide very detailed information on the spatio-temporal variations in a tank, but the method is costly. For this reason, CFD simulation techniques may be employed to provide such data at a lower cost. In recent years, both integrated experimental and CFD approaches have been used to determine flow field and to design various systems. Both CFD and LDV data reveal the existence of flow maldistribution caused by system design features, and these in turn show that the configurations that have, over the years, been regarded as standard may not provide the optimal operating conditions with regards to the system homogeneity and power consumption. The current trends in CFD studies point towards an increasing application of more refined grids, such as in large eddy simulation, to capture turbulent structures at microscales. This trend will further improve the quality of the simulation results for processes such as precipitation, in which micromixing and reaction kinetics are important.
Key words: simulation, mixing, hydrodynamics, CFD, stirred tank, LDV
Introduction
Mixing in stirred tanks is driven by the impeller-generated convective motion at larger scales, by turbulent transfer at smaller scales and diffusion at molecular scales.1 Smith2 reported that the lack of a fundamental understanding of the processes in stirred vessels leads to losses in the order of US$10 billion per year due to non-optimal energy utilisation. Thus, there is a need to identify and quantify the operating hydrodynamic parameters that influence the quality of mixing. This can be done by using both experimental3,4 and simulation methods.5 Experimental methods have typically been used to study the hydrodynamics in mixing tanks, and the interpretation of the data can be enhanced if there is an understanding of the physics of the flow. In this regard, mathematical models based on experimental data or on the fundamental principles of fluid flow have been employed to obtain detailed information on the flow field, and this enhances the understanding of the mixing mechanisms involved. Computational fluid dynamics (CFD) method, which is based on partial differential equations describing fluid flow, has proved to be a useful tool for studies of system hydrodynamics, especially during the last ten years.6–8
Measurements of mixing time and circulation time can be used to investigate the macroscale mixing performance of a stirred tank resulting from the bulk fluid flow.5 These mixing parameters do not account for spatial variations, which are the characteristic features of stirred tanks. Information on these spatial variations can be obtained using high precision measurement techniques, such as the laser Doppler velocimetry (LDV).4,9 However, this technique is only applicable to translucent tanks and fluid, which are not suitable for most chemical engineering applications. These technical limitations can therefore preclude the use of such a method to study the influence of hydrodynamics on reactor performance in many industrial applications. Experimental methods, however, still provide useful data for validation of simulation results. The present review focuses on singlephase systems with minimal reference to multiphase systems.
Experimental methods
Until about twenty years ago, and due to computational limitations, mixing studies were largely carried out using experimental methods. The studies were aimed at determining optimal tank geometries and impeller type.4,10 More recently, the experimental methods that have been employed, such as the LDV, focus on the measurement of the flow field, which is comparable to that of the CFD simulation method. The limitation of the LDV method is that it cannot be used to generate data in an opaque system, like stainless steel, which is a material of choice for many reactors. In this regard, the application of CFD simulation techniques to generate flow field in such a system, and the validation of fluid flow in an identical but transparent vessel, can provide insight into the hydrodynamics of a reactor.
Reactor geometry
In some studies, high precision equipment, such as hot-wire anemometry, digital particle image velocimetry and LDV, have been employed to study the flow field in a stirred tank. The studies have shown that there is a complex interaction between the tank geometry and the impeller performance. Mixing tanks can have a flat-or profile-based bottom, and the degree of the bottom curvature depends on the intended operation. Flatbottomed stirred tanks are commonly used for liquid systems, while elliptically or dished-bottomed tanks are used in solid– liquid or solid–liquid–gas systems to aid particle suspension. Many studies have been conducted in flat-bottomed tanks and with conventional impellers, such as the Rushton turbine, pitched blade impeller and flat-blade paddles. Relatively few studies have been done using round-or dished-bottomed tanks.
It is known that round-bottomed tanks enhance particle suspension by eliminating dead zones at the wall junctions.11 Dead zones, or regions of segregation, can be found at the wall junctions, especially for high aspect ratio tanks with flat bottoms. To reduce the dead zones in high aspect ratio tanks, the tank internals, such as baffles and draft tubes, are used to improve mixing. Similarly, multiple impellers12 have been employed to improve mixing in such systems. Configurations of the high aspect ratio tanks deviate from the standard ones, in which the liquid height is typically the same as the tank diameter for a tank stirred by a single impeller. The standard impeller diameter and its clearance distance from the bottom is one-third of its tank diameter.13
A large number of hydrodynamic studies has been conducted using these standard configurations and it recently has been shown that mixing can be improved with non-standard tank configurations.10,14 In a single-impeller stirred tank, the fluid flow in the lower part of the tank is largely dependent on the interaction between the downward stream and the tank bottom, which results in the generation of an upward jet. This jet is an important feature in a mixing tank and has attracted attention, especially with regards to solid–liquid mixing.15,16 The upward jet is influenced by baffles and it decays with an increase in tank height.
Baffles
Turbulent mixing is typically carried out in baffled tanks, which are usually equipped with four equally-spaced baffles with the width of the baffle usually being one-twelfth to onetenth of the tank diameter.13 In these tanks, power consumption increases with the number of baffles, but a decrease in the number of baffles results in poor mixing. Without baffles, swirl and central vortex formation may be experienced, which results in low shear rate, even if a high shear impeller, like the Rushton turbine, is used. Baffles change the flow patterns by converting part of the circumferential and radial velocity components into the axial velocity component.6,14 This enhances the axial circulation of the fluid, and at the same time introduces loops in the vicinity of the baffles. These loops can be suppressed by an increased upward current induced by a draft tube.
Draft tubes
The use of a draft tube introduces an additional wall in the system, the effect of which on the hydrodynamics is still not well understood, especially in tanks stirred using mixed-flow impellers. More detailed studies still are needed to determine the optimum draft tube configuration corresponding to tank and impeller geometries. The design parameters for a draft tube include the liquid level above the draft tube, bottom clearance and the ratio of draft tube diameter to that of the tank. In an earlier study, Oldshue13 recommended that the draft tube bottom clearance should be at least one draft tube diameter. The highest flow per power can be obtained by this device, especially if used in a fully baffled tank. A small draft tube cross-sectional area results in a high velocity in the draft tube. This leads to an increased head loss, which is a function of the square of the fluid velocity in the draft tube.13 Some recent studies have shown that draft reduces mixing time and power draw, whilst it improves axial mixing.14,17
Impellers
Impellers are classified either as axial or radial pumping, and the ones that do not fall into these two categories are referred to as mixed-flow impellers. The axial ones generate high flows while the radial ones are high-shear impellers. The choice of an impeller influences both capital and operation cost in mixing processes. The subsequent cost of operation depends on the power dissipated, and this is determined by the required level of homogenisation. Nienow3 performed mixing studies using different types of impellers and made a comparison between the performance of these impellers and the Rushton turbine.
Impeller types
Impellers are characterised by power number and pumping number, which are indicative of the circulation velocity and power draw, respectively. A retrofitting operation with constant power and impeller speed can be carried out to evaluate the relative influence of impeller geometry and pumping characteristics on the quality of mixing. It has been found that large impeller diameters are better for bulk mixing than large power number, small diameter ones.3
The Rushton turbine is the most widely used radial pumping impeller, for which the principal direction of discharge is normal to the axis of rotation. The impeller is typically made of six vertical blades bolted to a support disc and is used in applications that require high shear.13 It has been extensively studied in both single-phase13 and multiphase18 systems. Most impeller blades (such as those of the Rushton turbine) and baffles influence mixing at the mesoscale.
The axial impellers, which include the pitched-blade impeller and marine-type propeller, generate a high circulation flow. For solid–liquid systems, this enhances suspension of solid particles in the bulk liquid, and therefore increases the surface area of the particles available for mass transfer. A hybrid of axial and radial impellers is the mixed-flow impeller. These are later generation impellers which include the Lightnin A315 propeller,19 Chemineer, Maxflot-T and Erato Intermig.20 The Lightnin A315 propeller is used in systems where high circulation and high dispersive mixing are important, such as in gas–liquid systems.21 More recently, a lightning type of impeller (Mixtec HA735) was used to study mixing time.14
In some systems, more than one impeller may be required to provide efficient mixing. Multiple impellers are used in tanks with a high aspect ratio, where a single impeller may not generate momentum high enough to overcome the hydrostatic head. The multiple impellers may all be Rushton turbines,12 pitched blade impellers11 or a combination of the two types.19 In systems where the Rushton turbine is one of the impellers used, it is common practice for the lowest impeller to be a Rushton turbine.7 In this type of impeller assembly, the clearance between the respective impellers and the clearance from the tank bottom affect their performance. This clearance should be wide enough to avoid interference between the flow generated by the upper and lower impellers.
Impeller clearance
Most studies have been carried out at the standard impeller clearance (one-third of the tank diameter). Further, it has been shown that the impeller clearance does affect the fluid flow pattern.6 However, it has been reported that the flow pattern generated by the Rushton turbine changes from the typical two loops at a standard clearance to a single loop pattern at a low clearance. For a multiple impeller system, the optimal clearance at which there is minimal interference between the flow generated by the upper and lower impellers is equivalent to the tank diameter.12 Well-spaced impellers generate smooth and high fluid flows, which are characterised by mean velocity of the fluid and turbulence intensity.
Mean velocity and turbulent field
Turbulence and flow pattern
Mixing in stirred tanks is influenced by both the mean velocity and turbulent intensity. The turbulence structures and the bulk fluid flow pattern in general, have been studied for decades using parameters like flow number, mixing time and power number. In particular, it has been reported that trailing vortices behind the impeller blades influence the pumping capacity of the impellers.22 It is important to note that the mean flow parameters like the impeller power number, pumping number and mixing time, do not give detailed information on the level of turbulent field distribution and local pressure or concentration gradients, which influence mass transfer and, consequently, affect product quality. This has been the motivation for obtaining accurate data for the flow field using high-precision equipment.
Measurements of flow field
The mean flow field has been measured by methods such as hot-wire anemometry,23 hot-film anemometry,24 LDV25 and particle image velocimetry.26 The LDV and digital particle image velocimetry methods give more accurate data, but at a higher cost, which is one of the factors that limits the application of these methods. Laser Doppler velocimetry studies have shown that the interaction between the upward flow stream in a stirred tank and the free surface results in the formation of one vortex at the tank corner (where the free surface and the vertical wall meet)6 and a second vortex just below the region where the shaft and the free surface meet.27 Such hydrodynamic structures affect mixing quality.
Mixing and power
Measurements of mixing time
Experimentally, mixing time can be determined using a conductivity meter,28 pH meter18 or decolourisation method.29 For example, the mixing time required to achieve 90% homogenisation (t90) is the time it takes for the fluctuation of the response signal to be below 10% of the concentration achieved at perfect mixing, which is adequate for most systems. For the decolourisation method, the visual determination of the point at which the colour changes can be very subjective, and this compromises the reproducibility of such results. This is compounded by the fact that there is no unanimous agreement on the level of homogeneity that the decolourisation method gives. Kraume and Zehner4 took the decolourisation point to be equivalent to the 95% homogenisation level, whilst Bujalski et al.7 reported that decolourisation occurs at the 90% homogenisation level, obtained using a conductivity meter. Unfortunately, many authors do not report the level of homogenisation that decolourisation represents.
Effect of measurement techniques on mixing time
It has been reported that the location of a probe has no influence on mixing time.30 However, more recent studies show that the mixing time depends on the probe and injection locations,18 probe size19 and tracer concentration. Guillard and Tragardh18 found that a shorter mixing time could be obtained injecting at the top, compared to injecting at the bottom. However, even with a top injection, Otomo et al.31 obtained results which varied with radial location by as much as 100%. The quality of mixing must be evaluated on the basis of power required to achieve a given level of homogenisation. Homogenisation energy, which is a product of mixing time and the corresponding power dissipated, has been used to evaluate the mixing efficiency.19 Given the difficulties with experimental techniques, the CFD technique is an important tool that can be used to obtain such data, once the model has been validated.
Computational fluid dynamics simulation methods
The CFD simulation technique comprises grid generating, equation solving and result processing modules. A lot of effort has been devoted to the simulation and modelling of an impeller. Some of the most common approaches to modelling an impeller are impeller boundary condition,32 snap shot,33 sliding grid,34 multiple frames of reference35 and inner–outer.36 In a great number of these studies, impellers with simple geometries, such as the Rushton turbine, have been modelled. Modelling of curvedblade impellers poses a great challenge with regards to grid generation.
Grid generation and boundary conditions
For engineering design purposes, it is important to refine the grid to the extent that the simulation results are quantitatively and qualitatively comparable with experimental ones. Any further improvement in accuracy obtained with a finer grid may not deserve the additional computational cost required. The main factors to be considered in determining the grid size of a stirred vessel include: (a) boundary conditions, (b) impeller modelling approach, (c) model volume, (d) flow regime (turbulent or laminar), (e) the number of phases involved, (f) accuracy of results required and (g) computational resources. A summary of a sample of grid sizes for liquid only systems that have been reported in the literature is given in Table 1. A detailed description of the grid distribution for a stirred tank model has been given by Montante et al.6

Boundary conditions
The boundaries define the model volume which comprises the tank and impeller. The way boundary conditions like the impeller disc, blades, baffles and vessel walls are defined, determines the required grid size. The blades, disc and baffles may be defined as thin surfaces (2D)40 or surfaces with thickness (3D).35 In more recent versions of the CFD codes, there are wall functions that allow resolution of the boundary layer down to the wall. If present, draft tubes require special attention with regards to grid distribution, to account for the additional wall in the domain.
Model volume
There is a rapid increase in grid size (number of cells) with an increase in model volume for a given cell size. By decreasing the cell size, the control volume decreases, and this results in an increase in the value of the diffusion conductance at the cell face. This causes a decrease in the Peclet number, and enhances the resolution of the turbulent field. Murthy and Jayati40 employed 1 376 000 cells in a 0.79 litre tank to simulate the velocity field for a single-phase system.
Discretisation schemes and equation solvers
Dicretisation schemes and the equation solvers influence the precision and accuracy of the simulation results. However, the choice is constrained by the computational power available. In addition, the choice can be made on the basis of the dominating transport phenomena: convectional or diffusional mass transfer.
Discretisation schemes
The discretisation schemes that are widely used are upwind, power law, higher upwind, central differencing, hybrid and quadratic upstream interpolation for convective kinetics (QUICK). The upwind scheme is first-order accurate, and may be used to initiate a simulation. The hybrid discretisation scheme is formulated on the basis of the cell Peclet number, which gives the ratio of the convective flow to diffusion. The cell Peclet number depends on the flow and fluid properties:

where Pe is the Peclet number; ρ is the fluid density; u is the velocity; Γ is the diffusion coefficient; and Δx is the cell size. The third-order accurate scheme, QUICK, is obviously more computationally demanding than the others. Sahu and Joshi45 assessed the competitiveness of upwind, hybrid and power law schemes, and concluded that power law was the most robust of the three schemes. More recently, Aubin et al.46 compared upwind, higher order upwind and QUICK, and concluded that the best prediction of the circulation number was obtained with QUICK, followed, interestingly, by the upwind, and not the second-order upwind scheme as would be expected.
Solution algorithms
The pressure and velocity terms in the governing equations require coupling before the equations are solved. For a steady state flow, velocity-pressure coupling is done using algorithms, such as the semi-implicit pressure-linked equations (SIMPLE), SIMPLE-revised (SIMPLER), SIMPLE-consistent (SIMPLEC) and pressure implicit with splitting operators (PISO). Unlike the other schemes, SIMPLEC and PISO can be used in both steadyand unsteady-state systems. Sahu et al.43 employed both SIMPLE and SIMPLER and reported that simulation with higher grid sizes (finer grids) could not converge easily with SIMPLE.
Impeller modelling
Impeller boundary condition and inner-outer methods
The impeller boundary condition, being a black-box approach, requires input of experimentally determined velocity and turbulence quantities at the surface swept by the impeller, and it is the least computationally demanding approach. First, its major limitation is the dependency on experimental data. Therefore, the accuracy of the simulation is influenced by the accuracy of the experimental data used at the boundary. Second, boundary conditions are tank geometry specific. Therefore, data obtained in a given geometry may only be applicable to closely similar geometries.36 With the inner-outer approach, the vessel is subdivided into two partially overlapping zones, and an unmatched boundary is specified between the impeller tip and the baffles. It has been reported that the inner-outer approach gives a poor prediction of experimental results,6,36,44 and therefore, currently, it is less commonly applied.
Multiple frame of reference and sliding grid methods
In both multiple frame of reference and sliding grid approaches, no experimental data is needed; instead, the impeller is explicitly simulated. The multiple frame of reference and sliding grid approaches are similar in that in both cases the vessel is divided into two sub-domains: the inner sub-domain moves with the impeller, while the outer sub-domain is stationary with the baffles. The main limitations of the multiple frame of reference approach include: failure to account for the transient interaction between the impeller and the baffles, failure to predict the rate of decay of the local maximum velocity in the wall jet47 and inability to predict mixing time. In some applications, unbaffled tanks have been employed to simplify the numerical complexity involved in modelling the interaction between the baffles and the rotating impeller blades.39
The sliding grid approach enhances computational stability and accuracy by resolving the non-linearity at every time step. Due to the higher computational demand of the sliding grid approach compared to the multiple frame of reference approach, the sliding grid approach has been widely applied to single-phase systems,36 whilst the multiple frame of reference approach has been employed in multiphase systems and singlephase systems in which high density grids were defined.38 Montante et al.6 reported that the sliding grid approach produced better results with finer grids than the inner-outer one, such that beyond 160 272 cells, the inner-outer approach did not produce an observable improvement in the accuracy.
Turbulence modelling
The turbulence models based on the Reynolds-averaged Navier-Stokes equations fall into two categories, namely: eddy-viscosity model and Reynolds stress models. The twoequation eddy-viscosity models include the renormalisation group (RNG) k-ε, standard k-ε48 and k-ω49 models. Aubin et al.46 reported that there was no significant difference between the predictions of the velocity field obtained with the k-ε and RNG k-ε turbulence models. Hartmann et al.37 have shown that better prediction of the mean velocity and turbulent fields can be obtained with the large eddy simulation approach.
Mixing
Velocity field
The Reynolds-averaged Navier-Stokes equations are solved with the standard k-ε turbulence model, for which the continuity equation is:

where Ui is the mean velocity vector and ρ is the fluid density. The momentum equation is:

where p is the pressure; τij is the Reynolds stress; and FB represents the coriolis and centrifugal forces. For the multiple frames of reference approach, the transient terms are zero. However, the coriolis (Fc) and centrifugal (Fce) forces are important. The transient terms are retained in the case of the sliding grid approach.
Tracer transport
Mixing time can be obtained by solving the transient form of the hydrodynamics transport equation for a non-buoyant tracer given by:
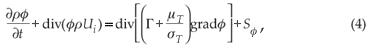
where ø is the tracer mass fraction; Γ and µT are the molecular and turbulent diffusivities, respectively; σT is the turbulent Schmidt number; and S ø is the source term. The CFD simulations for macromixing time can be compared with the corresponding empirical relations in the literature:
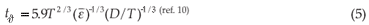
and
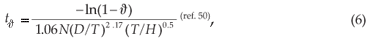
where  is the level of homogeneity (0<
is the level of homogeneity (0< <1) and, for the time (t95) required to achieve 95% homogeneity,
<1) and, for the time (t95) required to achieve 95% homogeneity,  = 0.95; T and D are the diameters of the tank and impeller, respectively; N is the impeller speed; and H is the liquid depth. Equations 5 and 6 are typically used to determine mixing time experimentally, while in CFD, Equations 2 and 3 are solved to obtain flow field, in which a simulated tracer is injected at one point and detected by a probe at another point. In this way, the CFD simulation results can be validated with the experimental ones.
= 0.95; T and D are the diameters of the tank and impeller, respectively; N is the impeller speed; and H is the liquid depth. Equations 5 and 6 are typically used to determine mixing time experimentally, while in CFD, Equations 2 and 3 are solved to obtain flow field, in which a simulated tracer is injected at one point and detected by a probe at another point. In this way, the CFD simulation results can be validated with the experimental ones.
Validation of simulation results and scale up
Among the experimental methods used to validate simulation results, LDV is currently one of the mostly widely employed methods because of its precision and accuracy. Simulation methods have been developed to link the typical experimental and theoretical approaches for investigating mixing features, such as wall jet, to the CFD simulation methods.15 The experimental methods for measuring mixing time have been successfully adopted in CFD simulation.5,7,40 Previously, the required computational power could not allow simulations with very fine grids. However, technology has improved in recent years and simulation of mixing time, using computationally intensive methods such as large eddy simulations, are increasingly being reported.8,51,52
Experimental validation of the simulations
It has consistently been shown over the years that in a stirred tank, the best prediction is obtained for the axial velocity component and the worst prediction is obtained for the kinetic energy dissipation rate.6,7,14 In addition, the same authors have reported that better prediction is obtained in the regions of high turbulence, such as the impeller region. Generally, there is a mismatch between the experimental and simulation results in the wall region. This can be attributed to the formation of small circulation loops at the junction of the baffles and the wall. The small circulation loops formed at the junction of the baffles and the tank wall are not well predicted by the k-ε model. It is therefore likely that the mismatch in the wall region could be as a result of the errors involved in the implementation of wall treatment algorithms (wall functions) and the anisotropic flows caused by the baffles.14 Predictions of the flow in the region closer to the surface of a mixing tank are generally poor and this has been attributed to the limitation of the k-ε model in representing the free surface.
Some simulation results indicate high velocity near the wall and these have been shown by experimental methods to represent the wall jet.16 A comparison of the numerical predictions with experimental data for the jet trajectories has been carried out by Torré et al.,53 and the results show a very good agreement. Their analysis of the transport of a passive scalar revealed the optimum injection conditions to maximise the mixing benefits of the bulk flow pattern. Recent studies show that the wall jet flow pattern can be enhanced by the use of a draft tube. It has been reported by Ochieng et al.,14 that the use of the draft tube resulted in a reduction of the mixing time by 23–50%, depending on the bottom clearance of the impeller. The typical design of a draft tube reactor is that the draft tube cross-sectional area is equal to that of the annulus.13 For these two cross-sectional areas to be equal, the diameter of the draft tube must be equal to 0.701 T. A draft tube of this diameter, that is centrally positioned in the tank, can be very conveniently defined on the stationary frame of the multiple frame of reference or sliding grid approach. For a draft tube diameter smaller than this, the superficial velocity is higher in the draft tube than in the annulus, and this results in a poor flow pattern, forming a double loop in the annulus; this is more pronounced when the draft tube diameter is less than 0.4 T.14
Scale up
Scale-up criteria depend on the impeller performance, flow regime, reactor geometry, phase hold-up and physical properties of the phases involved. Also, the scale-up criteria depend on whether the flow generated by the impeller is convective mixing or turbulent dispersion. A scale-up can be done on the basis of a constant impeller tip speed, which is related to the convective flow or specific power. Scale-up criteria can be given in the form of an equation:54

where N is the impeller speed; D is the diameter of the impeller; ko is a constant; and the exponent n depends on the process investigated. Wernersson and Tragardh55 employed multiple Rushton turbines in tanks of different sizes and concluded that scale-up with constant power was valid for the system. For example, flat-bottomed tanks scale-up with higher values of n compared to round-bottomed tanks.56
Conclusion
The quality of mixing is influenced by the performance of the mixing tanks, and this has been a subject of investigation for many years. Many impeller types have been employed to improve mixing in either a single-phase or multiphase system. However, the efficiency of mixing achieved in such systems depends on the geometry of the tank and impeller, as well as on the properties of the fluid. The conventional methods of evaluating the quality of mixing, namely of mixing time and power, may not provide sufficient information for the optimal design of such systems.
This review shows that modern techniques, such as LDV and CFD, can reveal the salient design features of the system. In particular, these studies have revealed mixing maldistribution features such as dead zones in the conventional stirred tank configurations. It has been further shown that the tank and impeller configurations that have over the years been regarded as standard may not provide the optimal operating condition with regards to system homogeneity and power consumption. The current research trend on stirred tanks shows that the simultaneous application of LDV and CFD techniques can provide detailed data for the system scale up. This can reduce the cost of a mixing process and improve product quality. The information on the fluid-flow pattern in tanks stirred by impellers mounted on multiple shafts still is lacking.
1. Nagata S. (1975). Mixing: Principles and Applications. John Wiley & Sons, New York. [ Links ]
2. Smith J.M. (1990). Industrial needs for mixing research. Trans. Inst. Chem. Eng. 68A, 3–6. [ Links ]
3. Nienow A.W. (1996). Mixing studies: a comparison of Rushton turbines with some modern impellers. Chem. Eng. Res. Des. 74A, 417–423. [ Links ]
4. Kraume M. and Zehner P. (2001). Experience with experimental standards for measurements of various parameters in stirred tanks: a comparative test. Trans. Inst. Chem. Eng. 79A, 811–818. [ Links ]
5. Javed K.H., Mahmud T. and Zhu J.M. (2006). Numerical simulation of turbulent batch mixing in a vessel agitated by a Rushton turbine. Chem. Eng. Process. 45(2), 99–112. [ Links ]
6. Montante G., Lee K., Brucato C.A. and Yianneskis M. (2001). Numerical simulations of the dependency of flow pattern on impeller clearance in stirred vessels. Chem. Eng. Sci. 56, 3751–3770. [ Links ]
7. Bujalski W., Jaworski Z. and Nienow W. (2002). CFD study of homogenization with dual Rushton turbine – comparison with experimental results II: the multiple frame of reference. Trans. Inst. Chem. Eng. 80A, 97–104. [ Links ]
8. Marchisio D.L. (2009). Large eddy simulation of mixing and reaction in a confined impinging jets reactor. Comput. Chem. Eng. 33(2), 408–420. [ Links ]
9. Mavros P., Mann R., Vlaer S.D. and Bertr J. (2001). Experimental visualisation and CFD simulation of flow patterns induced by a novel energy-saving dual configuration impeller in stirred vessels. Trans. Inst. Chem. Eng. 78A, 857–866. [ Links ]
10. Nienow A.W. (1997). On impeller circulation and mixing effectiveness in the turbulent flow regime. Chem. Eng. Sci. 52, 2557–2565. [ Links ]
11. Sharma R.N. and Shaikh A.A. (2003). Solids suspension in stirred tanks with pitched blade turbines. Chem. Eng. Sci. 58, 2123–2140. [ Links ]
12. Pinelli D. and Magelli F. (2000). Analysis of the fluid dynamic behaviour of the liquid and gas phases in reactors stirred with multiple hydrofoil impellers. Ind. Eng. Chem. Res. 39(9), 3202–3211. [ Links ]
13. Oldshue J.Y. (1983). Fluid Mixing Technology, p. 15. McGraw Hill, New York. [ Links ]
14. Ochieng A., Onyango M.S., Kumar A., Kiriamiti H.K. and Musonge P. (2008). Mixing and power draw in a tank stirred by a Rushton turbine at a low clearance. Chem. Eng. Process. 47(5), 842–851. [ Links ]
15. Bittorf K.J. and Kresta S.M. (2003). Prediction of cloud height for solid suspensions in stirred tanks. Chem. Eng. Res. Des. 81(A5), 568–577. [ Links ]
16. Jaworski Z. and Zakrzewska B. (2002). Modelling of the turbulent wall jet generated by a pitched blade turbine impeller: the effect of turbulence model. Chem. Eng. Res. Des. 80(8), 846–854. [ Links ]
17. Cate A., Denksen J.J., Kramer H.J.M., van Rosemalen G.M. and van den Akker H.E.A. (2001). Microscopic modelling of hydrodynamics in industrial crystallizers. Chem. Eng. Sci. 56, 2495–2509. [ Links ]
18. Guillard F. and Tragardh C. (2003). Mixing in industrial Rushton turbine agitated reactors under aerated conditions. Chem. Eng. Process. 421, 373–386. [ Links ]
19. Bouaifi M. and Roustan M. (2001). Power consumption, mixing time and homogenization energy in dual-impeller agitated gas-liquid reactors. Chem. Eng. Process. 40, 89–95. [ Links ]
20. Szalai E.S., Arratia P., Johnson K. and Muzzio F.J. (2004). Mixing analysis in a tank stirred with Ekato Intermig® impellers. Chem. Eng. Sci. 59, 3793–3805. [ Links ]
21. Bakker A. (1992). Hydrodynamics of stirred gas-liquid dispersion. Ph.D. thesis, Technical University of Delft, the Netherlands. [ Links ]
22. Ranade V.V. and Tayalia Y. (2001). Modelling of fluid dynamics and mixing in shallow bubble column reactors: influence of sparger design. Chem. Eng. Sci. 56(4), 1667–1675. [ Links ]
23. Ewing D.H., Hussein W.J. and George K. (1995). Spatial resolution of parallel hot-wire probes for derivative measurements. Exp. Therm. Fluid Sci. 11(2), 155–173. [ Links ]
24. Abel R. and Resch F.J. (1978). A method for the analysis of hot-film anemometer signals in two-phase flows. Int. J. Mult. Flow 4(5-6), 523–533. [ Links ]
25. Wu H. and Patterson G.K. (1989). Laser Doppler measurement of turbulentflow parameters in a stirred mixer. Chem. Eng. Sci. 44(10), 2207–2221. [ Links ]
26. Fan J., Rao Q., Wang Y. and Fei W. (2004). Spatio-temporal analysis of macro-instability in a stirred vessel via digital particle image velocimetry (DPIV). Chem. Eng. Sci. 59, 1863–1873. [ Links ]
27. Yianneskis M., Popiolek Z. and Whitelaw J.H. (1987). An experimental study of the steady and unsteady flow characteristics of stirred reactors. J. Fluid Mech. 175, 537–555. [ Links ]
28. Jaworski Z. and Pianko-Oprych P. (2002). Two-phase laminar flow simulations in a Kenics static mixer: standard Eulerian and Lagrangian approaches. Chem. Eng. Res. Des. 80(A8), 910–916. [ Links ]
29. Kuzmanic B. and Ljubicic N. (2001). Suspension of floating solids with up-pumping pitched blade impellers; mixing time and power characteristics. Chem. Eng. J. 84(3), 325–333. [ Links ]
30. Rao K.S.M.S.R. and Joshi J.B. (1988). Liquid-phase mixing: power consumption in mechanically agitated solid-liquid contactors. Chem. Eng. J. 39(2), 111–124. [ Links ]
31 Otomo N., Bujalski W., Nienow A.W. and Koji T. (2003). A novel measurement technique for mixing time in an aerated stirred vessel. J. Chem. Eng. Japan 36(1), 66–74. [ Links ]
32. Brucato A., Ciofalo M., Grisafi F. and Micale G. (1994). Complete numerical simulation of flow field in baffled stirred vessel: inner–outer approach. Inst. Chem. Eng. Symp. Ser. 136, 155–162. [ Links ]
33. Ranade V.V. and van den Akker H.E.A. (1994). A computation snap shot of a gas liquid flow in a baffled stirred reactor. Chem. Eng. Sci. 49(24B), 5175–5192. [ Links ]
34. Luo J.Y., Gosman D.A., Issa R.I., Middleton J.C. and Fitzgerald M.K. (1993). Full flow field computation of mixing in baffled stirred vessels. Trans. Inst. Chem. Eng. 71A, 342–344. [ Links ]
35. Luo J.Y., Issa R.I. and Gosman D.A. (1994). Prediction of impeller induced flow in mixing vessels using MFR. ICHEME Symposium Series 136, 549–556. [ Links ]
36. Brucato A., Ciofalo M., Grisafi F. and Micale G. (1998). Numerical prediction of flow fields in baffled stirred vessels: a comparison of alternative modelling approaches. Chem. Eng. Sci. 53(21), 3653–3684. [ Links ]
37. Hartmann H., Derksen J.J., Montavon C., Pearson J., Hamill I.S. and van den Akker H.E.A. (2004). Assessment of large eddy and RANS stirred tank simulations by means of LDA. Chem. Eng. Sci. 59(12), 2419–2432. [ Links ]
38. Bartels C., Breuer M., Wechsler K. and Durst F. (2002). Computational fluid dynamics applications on parallel-vector computers: computations of stirred vessel flows. Comp. Fluids 31(1), 69–97. [ Links ]
39. Alexopaulos A.H., Maggioris D. and Kiparissides C. (2002). CFD analysis of turbulence non-homogeneity in mixing vessels: a two-compartment model. Chem. Eng. Sci. 57(10), 1735–1752. [ Links ]
40. Murthy S. and Jayanti S. (2002). CFD study of power, mixing time for paddle mixing in unbaffled vessels. Trans. Inst. Chem. Eng. 76A, 482–498. [ Links ]
41. Nere K.N., Patwardhan A.W. and Joshi J.B. (2001). Prediction of flow in stirred tanks: new constitutive equations for eddy viscosity. Ind. Eng. Chem. Res. 40, 1755–1772. [ Links ]
42. Yoon H.S., Sharp K.V., Hill D.F., Adrian R.J., Balachpartar S., Ha M.Y. and Kar K. (2001). Integrated experimental and computational approach to simulation of flow in a stirred tank. Chem. Eng. Sci. 56(23), 6635–6649. [ Links ]
43. Sahu A.K., Kumar P. and Joshi J.B. (1998). Simulation of flow in stirred vessel with axial flow impeller: zonal modelling, optimisation of parameters. Ind. Eng. Chem. Res. 37, 2116–2130. [ Links ]
44. Harris C.K., Roekae D., Rosendal F.J.J. and Buitendijk F.G.J. (1996). Computational fluid dynamics for chemical reaction engineering. Chem. Eng. Sci. 51, 1569–1594. [ Links ]
45. Sahu A.K. and Joshi J.B. (1995). Simulation of flow in stirred vessels with axial flow impellers: effects of various numerical schemes and turbulence model parameters. Ind. Eng. Chem. Res. 34(2), 626–639. [ Links ]
46. Aubin J., Fletcher D.F. and Xuereb C. (2004). Modelling turbulent flow in stirred tanks with CFD: the influence of the modelling approach, turbulence model and numerical scheme. Exp. Therm. Fluid Sci. 28(5), 431–445. [ Links ]
47. Bhattacharya S. and Kresta S.M. (2002). CFD simulations of three-dimensional wall jets in a stirred tank. Can. J. Chem. Eng. 80(4), 695–709. [ Links ]
48. Launder B.E. and Spalding D.B. (1974). The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 3, 267–289. [ Links ]
49. Wilcox D.C. (2000). Turbulence Modelling for CFD. DCW Industries Inc., La Canada, CA. [ Links ]
50. Fasano J.B. and Penney W.R. (1991). Avoid blending mix up. Chem. Eng. Prog. 10(89), 56–63. [ Links ]
51. Yeoh S.L., Papadakis G. and Yianneskis M. (2005). Determination of mixing time and degree of homogeneity in stirred vessels with large eddy simulation. Chem. Eng. Sci. 60, 2293–2302. [ Links ]
52. Jahoda M., Motk M., Kukuková A. and Macho V. (2007). CFD modelling of liquid homogenization in stirred tanks with one and two impellers using large eddy simulation. Chem. Eng. Res. Des. 85(5), 616–625. [ Links ]
53. Torré J-P., Fletcher D.F., Touche I., Lasuye T. and Xuereb C. (2008). Jet injection studies for partially baffled mixing reactors: a general correlation for the jet trajectory and jet penetration depth. Chem. Eng. Res. Des. 86(10), 1117–1127. [ Links ]
54. Montante G., Pinelli D. and Magelli F. (2003). Scale up criteria for the solids distribution in a slurry reactor stirred with multiple impellers. Chem. Eng. Sci. 58, 5363–5372. [ Links ]
55. Wernersson E.S. and Tragardh C. (1999). Scale up of Rushton turbine-agitated tanks. Chem. Eng. Sci. 54, 4245–4256. [ Links ]
56. Chudacek M.W., Clift R., Grace J.R. and Weber M.E. (1985). Solids suspension behaviour in profiled bottom and flat bottom mixing tanks. Chem. Eng. Sci. 40(3), 385–392. [ Links ]
Received 9 February.
Accepted 25 August 2009.
* Author for correspondence E-mail: ochienga@vut.ac.za














