Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.105 n.9-10 Pretoria Sep./Oct. 2009
RESEARCH LETTERS
The applicability of existing topside ionospheric models to the South African region
P. SibandaI, II, *; L.A. McKinnellI, II
IHermanus Magnetic Observatory, P.O. Box 32, Hermanus 7200, South Africa
IIDepartment of Physics and Electronics, Rhodes University, P.O. Box 94, Grahamstown 6139, South Africa
ABSTRACT
The modelling of the electron density profile (Ne) for the topside ionosphere is challenging due to the limited availability of measured data. Over the past few years, a range of approaches to topside ionospheric modelling and representation of the Ne variation over the topside altitude range have been developed. This paper presents various topside ionospheric modelling efforts and describes their applicability for the South African region.
Key words: ionosphere, topside, electron density, vertical scale height, South Africa, modelling
Introduction
There is a need to improve our global understanding of the upper ionosphere and the accuracy of critical frequency maps which are used by high frequency (HF) radio engineers to calculate communication routes. Long-term models of the height distribution of electron density in the ionosphere are essential in the planning of HF radio propagation circuits1 and in assessing the effects of the ionosphere on Earth-space links. For example, a radio signal transmitted from a satellite to a ground receiver travels through this ionised medium; the effects on the propagating signal depend on the frequency and on the plasma density along the ray path. While significant progress has been made in bottomside ionosphere modelling for the South African region,2 very little has been done to assess the situation regarding topside altitudes. This paper presents an overview of topside modelling approaches and techniques and how they are applied in some of the existing topside ionosphere models. The specific goal of this study was to find a topside model and/or a modelling approach that best represents the topside over the South African region. Existing topside ionosphere models (IRI-2001 and NeQuick) were made available to the authors and are included for comparison with measured Ne profiles that were available for the South African region. Other topside ionosphere modelling approaches (such as theoretical modelling) that could possibly be useful for application in modelling the topside ionosphere over South Africa are also discussed. Unfortunately the models that apply the theoretical approach were not available to the authors and therefore no analysis was done to assess the applicability of this approach. This investigation was undertaken as a first step towards developing a South African topside ionosphere model that could be fitted to the current South African bottomside ionosphere model.2
An overview of the topside ionosphere
Figure 1 is an illustration of the different regions into which the ionosphere can be divided. The bottomside ionosphere lies below the F2 layer peak (hmF2), and the topside extends from the F2 peak to the upper transition height (UTH) – the transition height between the oxygen ion and hydrogen ion dominated plasma regions.3 The plasmasphere lies above the UTH, and for our purposes we consider the topside ionosphere to lie between hmF2 and the UTH.
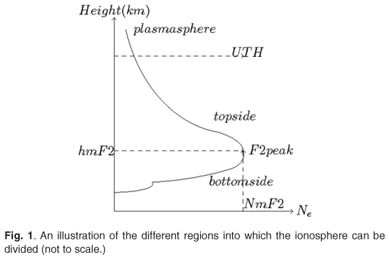
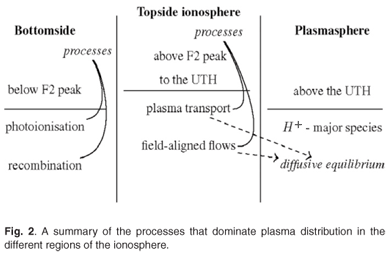
A summary of the processes that dominate plasma distribution in each region of the ionosphere is given in Fig. 2. In the bottomside ionosphere, chemical reactions (such as photoionisation, ion-molecular reactions and electron-ion recombination) dominate plasma distributions,3 while in the topside ionosphere, the plasma density profiles are largely determined by field-aligned plasma flows and the plasma transport process.4 Hydrogen is the major ion species in the plasmasphere, decreasing exponentially with altitude.5
Common topside modelling approaches
Topside ionosphere modelling suffers due to the poor availability of measured electron density data.6 Measuring the topside of the ionosphere requires a topside sounder system that is located above the ionosphere, ideally onboard a polar-orbiting satellite. Such missions are costly and are therefore difficult to undertake. Many attempts to develop a global representation of the altitude distribution of the electron density in the topside ionosphere have been made.7–11 The modelling efforts can be placed into two categories: (1) empirical models (models based on measurements) and (2) theoretical or first-principle models.
Empirical models
Empirical models have over the years been widely used to describe ionospheric behaviour and variation. For empirical models, simple mathematical functions are fitted to measured data which are usually binned with appropriate indices. Empirical models, therefore, represent 'average' and not instantaneous conditions.12 Some mathematical functions commonly used to reconstruct the electron density profile in the topside ionosphere are given below.
• The Chapman function:

where 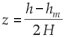 . This function can take one of two forms: an α-Chapman when c= 0.5 or a β-Chapman when c= 1, depending on assumptions related to the electron recombination theory.13
. This function can take one of two forms: an α-Chapman when c= 0.5 or a β-Chapman when c= 1, depending on assumptions related to the electron recombination theory.13
• Sech-squared (Epstein) function:
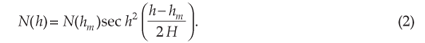
• Exponential function:

• Parabolic function:
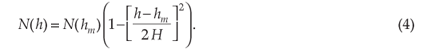
In each function, hm is the peak density height and His the vertical scale height, a key parameter in determining the shape of the electron density profile. Various methods of calculating the vertical scale height, such as the use of global positioning system (GPS)-derived total electron content (TEC),13,14 have been developed. The topside vertical scale height can also be obtained from ground-based ionosonde measurements,15 where it is estimated from the shape of the bottomside profile at the F2 peak and assumed constant throughout the topside. Other studies10,16 have used topside sounder data to determine the topside vertical scale height. Some of the empirical ionospheric models available are summarised below.
• The International Reference Ionosphere (IRI) model gives a global representation of the topside, amongst other things. It has been updated and improved regularly since it was first created in the 1960s. The altitudinal variation of the electron density in the topside is based on the topside sounding records of the International Satellites for Ionospheric Studies (ISIS) and Alouette topside sounders, and is described by simple mathematical functions (such as the Booker function),17 whereby different sections are modelled with a constant scale height, represented analytically as an exponential layer (as described by Equation 3).18
• The NeQuick model8 describes the topside electron density profile as an Epstein layer.19 It applies the Di Giovanni and Radicella (DGR) 'profiler' concept, a concept that uses an Epstein function (Equation 2) whose shape is controlled by an empirical parameter connected to the bottomside thickness parameter, originally introduced by Di Giovanni and Radicella20 and later modified and improved by Radicella and Zhang.8 The model is based on bottomside ionosonde measurements and the ISIS and Intercosmos 19 topside sounder measurements.
• A variety of international organisations and groups have conducted topside modelling programmes. These include: (1) the Royal Meteorological Institute of Belgium,9,13,21 who have used GPS-based TEC, bottomside ionosonde measurements and empirically obtained oxygen-hydrogen ion transition height values to reconstruct the electron density profile in the topside ionosphere. The topside electron density is considered the sum of the constituent oxygen and hydrogen ion densities with unknown vertical scale heights. The reconstruction procedure involves incorporating a suitable ionospheric profiler (Chapman, Epstein or exponential) into equations describing ionospheric conditions, such as plasma quasi-neutrality and ion transition level, to analytically approximate the individual major ion density distributions of the oxygen and hydrogen ions. This gives a system of transcendental reconstruction equations that can be solved numerically to get the electron density profile. (2) Pulinets etal.11 and Depuev and Pulinets,16 from the Institute of Terrestrial Magnetism, Ionosphere and Radiowave Propagation of the Russian Academy of Sciences (IZMIRAN), have used topside sounder data from the Intercosmos 19 satellite to develop a global empirical model of the topside ionosphere for disturbed conditions. They approximated the electron density profile using an Epstein function with the altitude-dependent F2 layer thickness parameter.
Comparison with measured profiles
Predicted topside profiles from the IRI and the NeQuick models were compared with measured profiles to determine how accurately the models represent the topside over the South African region, with an emphasis on the shape of the topside profile. The ISIS database of topside profiles (accessible through the web; ftp://nssdcftp.gsfc.nasa.gov/spacecraft_data/isis/) was used for comparison with model results. Sample profiles that fell during the daytime sector were chosen from the database for comparison with model results. Efforts to select profiles that fell on the same UT time for the different months used for analysis failed due to the paucity of data from the South African region within the database. Such data are scarce due to a number of reasons—the satellite had no onboard memory and coverage depended on the distribution of ground receiver stations, and also the fact that, generally, satellite data exist as sets of points along the path of the satellite. The local times for the profiles ranged from 08:00 to 14:00, with each profile taken at a different local time within that range. The IRI-2001 and NeQuick topside models were computed for the corresponding times of the measured profiles.
The models were used in their original form with an emphasis on how well they represented the topside ionosphere over the South African region. For the IRI-2001 model, measured peak parameters (the critical frequency of the F2 layer (foF2) and the maximum height of the F2 layer (hmF2)), as measured by the topside sounder, were used as anchor points in order to adapt the model to the ionospheric conditions of the measured electron density profile and concentrate the analysis on the profile shape. The IRI-2001 model has the ability to adapt to ionospheric conditions on the basis of measured peak parameters. The NeQuick model profiles were, however, determined without any adjustments. Figure 3 shows the model results compared with the measured Neprofiles. The electron density in the profiles shown in Fig. 3 has been plotted on a log scale in order to highlight the differences in a clearer way.
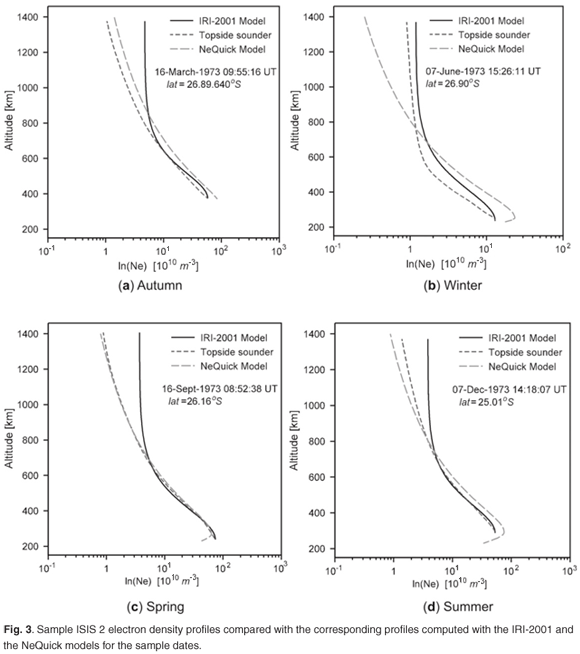
These results show, in general, how accurately the models represent the variation of the electron density as a function of altitude. The sample profiles used were chosen to illustrate the ability to predict during different seasons. Both models follow the shape of the measured profile but the IRI-2001 model overestimated the measurements at higher altitudes (above about 800 km) in three (autumn, spring and summer) of the four cases. The NeQuick model, on the other hand, corresponded well to the measured data at higher altitudes but overestimated the measurements at lower altitudes. The IRI-2001 model performed better than the NeQuick model at lower altitudes in three of the four cases, which could be because the IRI-2001 model assimilates additional information about the peak.
The challenge regarding applicability of an empirical approach for the South African region is the amount of measured data available andhowit is distributed under the various geophysical conditions. Coverage of the very first sounding satellites (Alouette and ISIS) depended on the distribution of ground receiving stations because they had little memory capacity and no onboard processing capability. As an example of the sparsity of the database, Table 1 shows the available ISIS 2 topside sounder electron density profiles for the southernAfrican region and how they are distributed over the four years for which data are available.

Theoretical models
Theoretical or first principle models can be used to represent the behaviour of the ionosphere.
This approach involves modelling the physical and chemical processes that are thought to be the major drivers of the distribution of the electron density in the given ionospheric region. For example, the continuity, momentum and energy equations for the electrons and ions are solved as a function of altitude and/or along magnetic field lines to determine the electron density.12 The assumption is that the calculated electron densities actually describe the variation in the real ionosphere.
Theoretical models based on the principles described above have been developed. For example, Titheridge22 developed a procedure for calculating the electron density profile in the topside ionosphere through the 'diffusive equilibrium' approach. In this approach, the topside ionosphere is assumed to be composed of the major ions, O+ and H+. He simplified the diffusive equilibrium equations, such that the scale height is given by
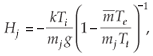
where k is the Boltzmann constant, Ti is the ion temperature, mj is the jth ion mass, g is the gravitational acceleration, 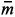 is the mean ion mass, Te is the electron temperature and the total temperature is Tt = Ti + Te. Given the number density nj0 at the height h0, the density nj at some greater height h0+ Δh is calculated from
is the mean ion mass, Te is the electron temperature and the total temperature is Tt = Ti + Te. Given the number density nj0 at the height h0, the density nj at some greater height h0+ Δh is calculated from
njTt =njoTto exp (–Δh/Hj).
This form is suitable for numerical integration, such that, in a series of small altitude 'steps', the density of a given ion species at greater height can be calculated if its density at a certain base height is known.23 Webb and Essex23 used this approach to develop an ionosphere/plasmasphere model, modified in such a way that:
(i) Chemical equilibrium is used to model the H+ ions at lower altitudes and then diffusive equilibrium is used for the upper ionosphere and plasmasphere.
(ii) The diffusive profiles are calculated along the field lines, rather than simply in the vertical direction, because the plasma is constrained to move along magnetic field lines.
The advantage of the theoretical approach in modelling the ionosphere is that the response of the system to magnetospheric phenomena, such as magnetic storms and substorms, can be modelled. The main disadvantage of the theoretical approach is the extensive computing power required and the fact that the models depend on a large number of magnetospheric inputs, such as electric fields, that may not be well known.12,24 Models that are based on theoretical considerations were not available at the time this study was conducted and, therefore, analysis to test how such models represent the topside ionosphere in the South African region was not possible.
Conclusions
The major goal of our study was to find a topside ionosphere model or modelling technique suitable for the South African region. It is our intention that the model then be applied to the South African bottomside electron density model, such that a user can specify the location (and other essential parameters and conditions) and have the model accurately determine the electron density profile – from 90 km to approximately 1 000 km. In this present study, various approaches to topside modelling were identified and described, and a few existing models were tested to see how they performed in the South African region.
The empirical modelling approach has been widely used and is probably the most practical for ionospheric applications. However, since the approach relies on the availability of good-quality measured data, the ionospheric variations may be misrepresented where data are not available. Theoretical models are a potential option for topside modelling and can provide an understanding of the natural variabilities. It is foreseen that, in the short term, an approach to topside ionosphere modelling for South Africa will include both an empirical and a theoretical component until such time as more measured data become available.
We wish to thank the National Space Science Data Centre (NSSDC) for making the ISIS 2 topside data available on CD and the Abdus Salam International Centre for Theoretical Physics, Trieste, Italy, for allowing access to the NeQuick model.
1. Bradley P.A. and Dick M.I. (1997). Use of ground-based and satellite data for an improved procedure for testing the accuracy of ionospheric maps. Technical Report, Rutherford Appleton Laboratory, Chilton, Didcot, Oxon, U.K. [ Links ]
2. McKinnell L.A. (2002). A neural network based ionospheric model for the bottomside electron density profile over Grahamstown, South Africa. Ph.D. thesis, Rhodes University, South Africa. [ Links ]
3. Marinov P., Kutiev I. and Watanabe S. (2004). Empirical model of O+–H+ transition height based on topside sounder data. Adv. Space Res. 34, 2015–2022. [ Links ]
4. Venkatraman S. (1999). Nighttime behaviour of the equatorial topside ionosphere. Ph.D. thesis, University of Texas at Dallas, Texas. [ Links ]
5. Yoshimura R., Maruyama T. and Kawamura S. (2005). Application of dynamical equilibrium model to topside ionosphere specification. In Proceedings of the XXV111 URSI General Assembly, New Delhi. [ Links ]
6. Huang X., Reinisch B.W., Bilitza D. and Benson R.F. (2002). Electron density profiles of the topside ionosphere. Ann. Geophysics 45, 125–130. [ Links ]
7. Reinisch B.W. (2004). Tenth International Digisonde Training Seminar at UMass Lowell reviews state of real time mapping of the ionosphere. IEEE Antennas Propag. Mag. 45, 110–117. [ Links ]
8. Radicella S.M. and Zhang M.L. (1995). The improved DGR analytical model of the electron density height profile and total electron content in the ionosphere. Ann. Geophys. 38, 35–41. [ Links ]
9. Stankov S.M., Warnant R. and Jodogne J.C. (2002). Operational model for real-time reconstruction of the electron density profile using GPS TEC measurements. In Proceedings of the XXVII URSI General Assembly, Maastricht, the Netherlands. [ Links ]
10. Kutiev I.S., Marinov P.G. and Watanabe S. (2006). Model of topside ionosphere scale height based on topside sounder data. Adv. Space Res. 37, 943–950. [ Links ]
11. Pulinets S., Depuev V., Karpachev A., Radicella S. and Danilkin N. (2002). Recent advances in topside profile modeling. Adv. Space Res. 29, 815–823. [ Links ]
12. Schunk R.W. and Sojka J.J. (1992). Approaches to ionospheric modelling, simulation and prediction. Adv. Space Res. 12, 317–326. [ Links ]
13. Stankov S.M., Jakowski N., Heise S., Muhtarov P., Kutiev I. and Warnant R. (2003). A new method for reconstruction of the vertical electron density distribution in the upper ionosphere and plasmasphere. J. Geophys. Res. 108, 1164. [ Links ]
14. Jakowski N., Kutiev I.S., Heise S. and Wehrenpfennig A. (2002). A topside ionosphere/plasmasphere model for operational applications. In Proceedings of the XXVII URSI General Assembly, Maastricht , the Netherlands. [ Links ]
15. Huang X.Q. and Reinisch B.W. (2001). Vertical electron content from ionograms in real time. Radio Sci. 36, 335–342. [ Links ]
16. Depuev V.H. and Pulinets S.A. (2004). A global empirical model of the ionospheric topside electron density. Adv. Space Res. 34, 2016–2020. [ Links ]
17. Coïsson P. and Radicella S.M. (2004). The IRI topside parameters. Adv. Space Res. 2, 249–251. [ Links ]
18. Bilitza D., Reinisch B.W., Radicella S.M., Pulinets S., Gulyaeva T. and Triskova L. (2006). Improvements of the International Reference Ionosphere model for the topside electron density profile. Radio Sci. 41, 1–8. [ Links ]
19. Coïsson P., Radicella S.M. and Nava B. (2002). Comparisons of experimental topside electron concentration profiles with IRI and NeQuick models. Ann. Geophys. 45, 125–130. [ Links ]
20. Di Giovanni G. and Radicella S.M. (1990). An analytical model of the electron density profile in the ionosphere. Adv. Space Res. 10, 27–30. [ Links ]
21. Stankov M.S. and Muhtarov P.Y. (2001). Reconstruction of the electron density profile from the total electron content using upper transition level and vertical incidence sounding measurements. C. R. Acad. Bulg. Sci. 54, 45–48. [ Links ]
22. Titheridge J.E. (1972). Determination of ionospheric electron content from the Faraday rotation of geostationary satellite signals. Planet. Space Sci. 20, 353–369. [ Links ]
23. Webb P.A. and Essex E.A. (1999). Modelling the Plasmasphere. Online at: http://www.ips.gov.au/IPSHosted/STSP/meetings/aip/phil/phil.htm [ Links ]
24. Cander L.R., Leitinger R. and Levy M.F. (1998). Ionospheric models including the auroral environment. In Proceedings of the ESA Workshop on Space Weather, ESTEC, Noordwijk, the Netherlands. [ Links ]
Received 10 April 2008. Accepted 8 July 2009.
* Author for correspondence E-mail: psibanda@hmo.ac.za














