Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.105 no.9-10 Pretoria Set./Out. 2009
RESEARCH ARTICLES
Experimental response of an optical sensor used to determine the moment of blast by sensing the flash of the explosion
A. RouxI, *; G.N. NurickII
ICouncil for Scientific and Industrial Research, 5 John Costas Street, Plankenbrug, Stellenbosch 7600, South Africa
IIBlast Impact and Survivability Research Unit, Department of Mechanical Engineering, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
ABSTRACT
The Council for Scientific and Industrial Research (CSIR) conducts research into the effect of underwater explosions on maritime structures and equipment. One of the parameters that are required to be measured to a large degree of accuracy is the shock wave velocity in close proximity (10–120 charge radii) of the explosion, without having to revert to the streak photography method. This distance is in the region where the near field crosses over to the far field, and it would be expected that the distance–time curve would not be linear. The streak photography method produces accuracy in the very near field of the explosion, but is not recommended for accurate measurements at distances beyond 20 charge radii. We investigated the response of an optical sensor constructed to measure the light flash of an underwater blast to determine the moment of explosion. By measurement of the time taken between this moment and the time when the shock wave reaches the pressure sensors, accurate measurements of the distance–time history (and hence shock wave velocity) could be calculated. Twelve general purpose phototransistors were used in a parallel configuration to enhance the sensitivity of the sensor. These transistors were connected directly to a conditioning amplifier which formed the interface between the transistors and the data acquisition equipment. The results that were obtained confirmed that the light intensity of the flash of the explosion increased to a maximum within several microseconds. Measurements of the average velocity of the shock wave propagation, based on the flash measurement as a marker, correlated to within 0.1%, meaning that this method of marking the moment of explosion to within several microseconds had been successful. This method can therefore be used in similar underwater blast measurement applications when a measurement marker of the moment of explosion is required.
Key words: underwater explosions, underwater blast, optical sensor, light sensor, shock wave propagation velocity measurement, distance-time measurements
Introduction
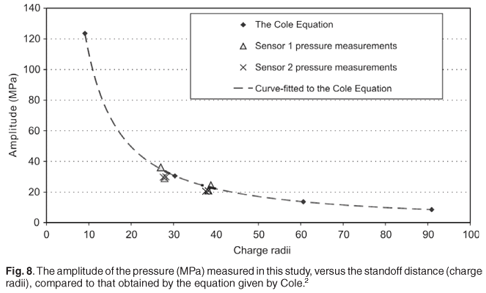
The Council for Scientific and Industrial Research (CSIR) conducts research into the effect of underwater explosions on maritime structures, as well as on equipment containing electronics, in close proximity of the blast. An underwater blast can have devastating effects on fixed structures and ships because explosives have greater effect in water than in air. Two factors contribute towards the damage to structures and equipment; these are the pressure caused by the shock wave, and the secondary pressure of the expanding and contracting gas bubble caused by the explosion. The pressure–distance function therefore needs to be determined to predict damage to equipment at a specific standoff distance. It is known that the pressure in close proximity to the blast is extremely difficult and impractical to measure because the amplitude of the shock wave is in the gigapascal range. Engineers therefore rely mainly on data previously reported, for example the pressure at the border condition given by Cooper1 and the pressure history given by Cole2 (accurate only for distances greater than a scaled distance of 50 charge radii).
To predict damage to structures or equipment at distances ranging from the border condition (0 charge radii) up to several hundreds of charge radii, a different approach to determine the pressure–time or pressure–distance function for the required standoff position of less than 50 charge radii (depending on the interest of the researcher) is needed. This different approach is extracted from both Cooper1 and Kira et al.,3 who give the relationship between pressure and shock wave velocity, described by Equations 1 and 2.

where P = pressure function, P0 = atmospheric pressure, ρ0 = density of water (1 000 kg m–3 for pure water at P0), Us= shock wave velocity, and up = particle velocity.

where C0 is the speed of sound in the medium, and s is a constant, depending on the type of explosive used.
Substitution of up in a rearranged Equation 2 into Equation 1, gives an equation which gives pressure as a function of shock wave speed (Equation 3). Therefore, if the shock wave speed can be measured in the near field, then the pressure can be calculated. This equation is assumed to be true for Us> C0, because when sup= 0 (therefore Us= C0), then the shock wave pressure is equal to atmospheric pressure, which is not true in close proximity to the explosion.

Kira et al.3 used a shadow graph method to obtain the time– distance function (inclusive of speed information) of the shock wave from the boundary condition to approximately 12 charge radii. The shadow graph method (also called the streak photography method) was not available for the purposes of this study; however, for practical reasons, the method seems to give a high degree of accuracy only for shock wave travel distances up to 50 mm, and hence was not deemed to be applicable in the context of this study which focused on greater distances. The focus of this study was to obtain pressure (velocity) information between 10 charge radii and 120 charge radii (just less than 1 m for a 30 g charge of plastic explosive (PE4)), where instrumentation containing electronics were to be placed. These distances are deemed to be within the crossover region of the near field to the far field of an underwater explosion.
As a result of the relationship between the pressure of the shock wave and the shock wave velocity, and taking cognisance of the difficulty of pressure measurement, we also measured velocity.
Obtaining velocity data in close proximity of the blast requires a high degree of accuracy in the determination of the 'moment of blast'. During previous executions of the measurement of time-related incidents during underwater explosions, some difficulty was experienced in accurately correlating the recorded data to the moment of the explosion, due to the inaccurate synchronisation of the method that was used to trigger the measurement equipment.
The synchronisation was achieved previously by measurement of the current flow through the detonator. Some detonators have characteristics which render this method practical for some applications, but for most, the time difference between the detonator current and the actual main charge to complete the detonation function varies too much to make accurate measurements of the shock wave propagation velocity in the near field.
This experiment investigated the possibility of using a photo-transistor (or array of phototransistors) to sense the flash that is produced when an underwater explosion occurs. Given that light travels much faster than any other known phenomenon in a transparent medium, the measurement of the flash of the explosion is a good method to determine the moment of explosion.
To validate the measurements, the average shock wave velocity was determined by the measurement of the shock wave pressure at predetermined positions, while using the light measurement as a time marker. A good correlation between blast events would mean that a solid time marker had been obtained, which would validate the postulation that the optical (or light) sensor was successful in this experiment.
Methods
An optical sensor was designed to give a high (10 V) voltage output when the flash of the explosion occurred. In the dark water, the optical sensor had a low voltage output (close to 0 V). The amount of light to be expected from a light flash of an explosion was unknown; therefore the methodology included repetitions with altered designs in the event that the first estimation proved to be incorrect.
The experiment was designed to place two pressure sensors in close proximity of a 30 g PE4 charge, and to place the optical sensor at a distance of approximately 0.5 m from the charge. Five blast events were planned for this experiment—two for which the two pressure sensors were placed at the same distance from the blast as the optical sensor, and three for which the pressure sensors were placed at greater distances from the blast. The distance–time data of a blast event in a previous experiment using the same setup (but with the sensor at a greater distance), were also incorporated into this experiment. The rationale was to calculate the average propagation velocity of the shock wave by using the time taken from the moment of the explosion, as measured by the optical sensor, and the time taken for the shock wave to arrive at the pressure sensors at two positions from the blast. The experiment would be considered successful if the calculation of the average shock wave velocity (or distance–time relationship) between the equidistance points was within 1% of each other, and the light sensor output gave a sharp rising edge <5 µs, which could be used as the time marker for the blast event.
Experimental setup
This experiment was planned to coincide with another experiment where the charge sizes and available standoff distances would be favourable for this experiment to succeed. Therefore, the mechanics for this experiment differ somewhat to what would be expected under different circumstances.
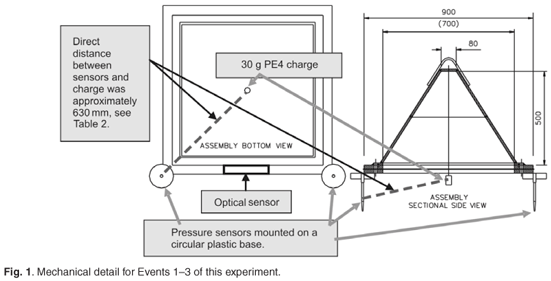
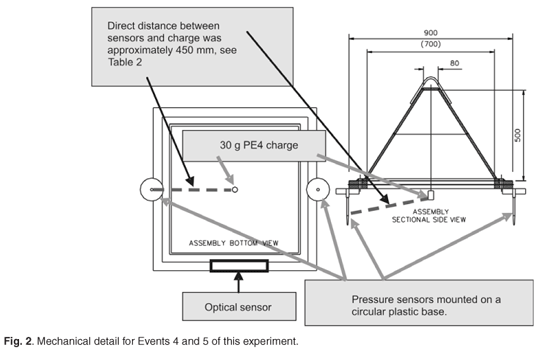
For all blast events a 30 g PE4 charge was mounted at the centre of the bottom plate (see Figs 1–3). For Events 1–3, the pressure sensors were mounted close to the outer corners of the pyramid base. The optical sensor was mounted on the side of the frame in the middle (Fig. 1). For Events 4 and 5, the pressure sensors were mounted on the side of the frame in the middle, as was the optical sensor (see Fig. 2).

Equipment
The optical sensor. One of the characteristics of a shock wave that is known to contribute to damage inflicted upon a blast-loaded object (e.g. a ship's hull), is the shock wave pressure, and therefore also the speed at which the shock wave propagates (Equation 3). At the boundary condition, where the shock wave is transmitted from the exploded mass to the surrounding water, the speed of the shock wave is at its highest value.1,4 The measurement of the speed of the shock wave has therefore become an important variable in the determination of damage resulting from the blast characteristics. This experiment measured the average speed of the shock wave at two standoff distances, using a custom optical sensor to determine the time origin of the explosion by capturing, and marking the commencement of, the light that the exploding material produced.
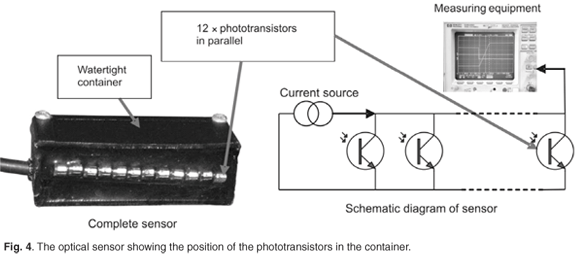
The optical sensor consisted of a string of 12 optically-sensitive transistors, connected in parallel (Fig. 4). The transistors were connected to a 20-m RG58 coaxial cable with Bayonet Neill Concelman connector (BNC) termination, and potted with Elite FR-766 polyurethane potting in a small plastic holder. The optical sensor was directly powered by the conditioning amplifier, which was adjusted to deliver a constant current of 17 mA to the sensor. When the flash of the explosion occurred, the light produced by the explosion reduced the forward resistance of the parallel transistors. It was expected that the explosion of 30 g of PE4, at standoff distances between 400 mm and 700 mm, would produce more than adequate photons to push the sensors into their saturation limit before being disturbed by moving water. The sensors were designed to produce a sharp-rising leading edge when the light was applied; no changes in light intensity were required when the sensor was in the saturation mode. The change in the transistor resistance was transformed by the signal conditioner and passed to its output as a voltage, which was measured by the data acquisition equipment.
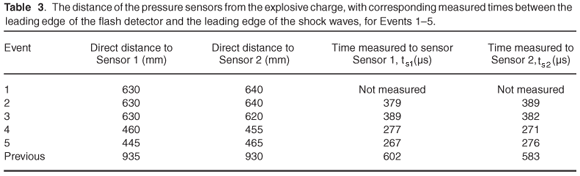
The optical sensor was placed on the side of the test sample in a position where it could sense the flash, yet not be damaged by the blast. It was secured onto the test sample by using double-sided adhesive tape (approximately 3 mm thick) to enable it to tear loose during the explosion without sustaining damage. Figure 5 shows the position of the optical sensor on the underside of the test unit, relative to the charge position. The position of the pressure sensors were moved from the position shown in Fig. 5 (for Events 2 and 3) to a position nearer to the explosive charge, as shown in Fig. 6, for Events 4 and 5.


Signal conditioner and amplifier. The signal conditioner used was a PCB Piezotronics model 482A22. The pressure sensors had built-in charge amplifiers, and were supplied with the required power by the conditioning amplifier, which also supplied a constant current to the photosensor.
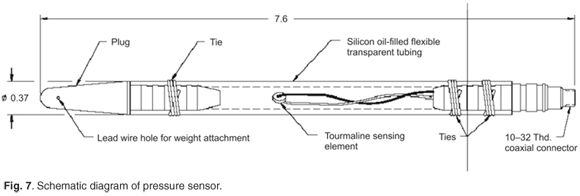
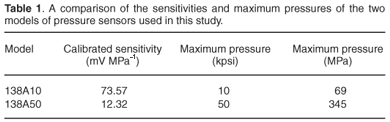
Pressure sensors. To measure the pressure amplitudes of the explosions at certain standoff distances, two tourmaline piezoelectric sensors with built-in charge amplifiers were used; these sensors were specially designed for the measurement of pressure shock waves as produced by an underwater blast. The sensor assembly is shown in Fig. 7. Two models were used: 138A10 and 138A50. The only difference between the two models was their sensitivity (Table 1). A 25-m long RG58C/U coaxial cable was attached to each sensor via a connector at both ends. To measure the explosion pressure, the sensors and cables were connected to a PC expanded interface (PXI)-format data acquisition card, capable of measuring four channels, with each channel sampling at 2 MS s–1.
Custom synchronisation equipment. The measurement-recording equipment was fitted with memory to record only 1 s of data in the four channels. Keeping in mind that the optical sensor was under investigation in this study, another measurement-cycle trigger had to be found which would trigger the measurement event before the explosion flash was expected (pre-trigger). For this purpose, a custom trigger unit was developed that would trigger the measurement event when the electrical current through the detonator exceeded a threshold, which would generate a logic trigger pulse.
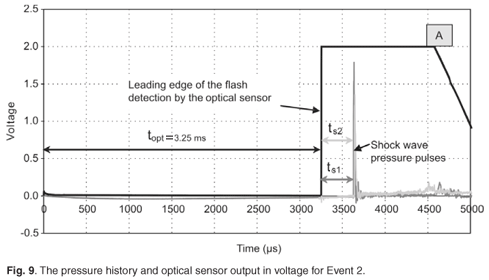
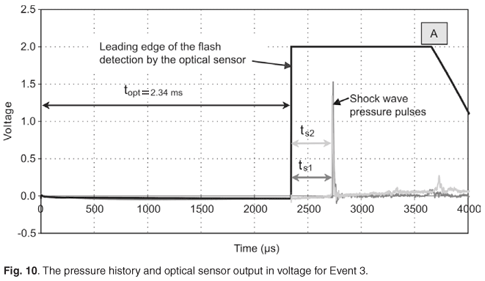
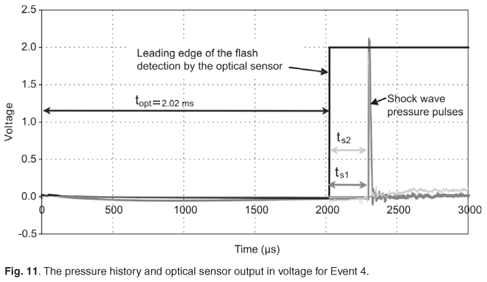
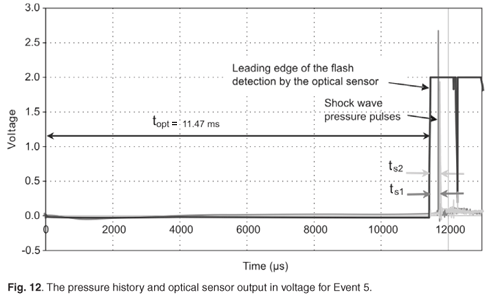
This logic trigger pulse was fed to the data acquisition equipment as an external trigger for the measurement cycle to start. It was expected that the time between this moment and the time for the main charge to produce a flash would be milliseconds, which would produce enough pre-flash information to be able to assess the operation of the optical sensor. The pre-flash history is shown in Figs 9–12, from which it was established that the time between the initiation of the detonator and the production of the explosion flash ranged from 2.024 ms to 11.467 ms . The large variation in these times precluded this synchronisation method from being used as a time-of-explosion marker, but allowed a reliable method for starting the measurement cycle which would include a few milliseconds of pre-flash information.
A PXI computer containing a 4-channel data acquisition card was used, in a configuration for measurement at 0.5-µs intervals.
Results
A total of five charges were detonated for the experiment. Measurement results were obtained for only four events. The first event experienced a sub-system power loss, and no data was recorded. Data for Events 2–5 were recorded successfully.
Pressure measurements
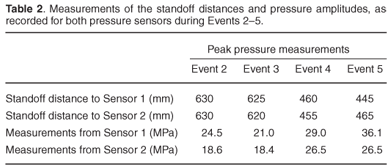
Pressure measurements were recorded by two pressure sensors per event. For Events 2 and 3, the pressure sensors were positioned at the corners of the test jig, giving a direct (measured) linear distance from the charge to the sensors approximating 625 mm and 635 mm, respectively (see Fig. 5 for the position of the pressure sensors and Table 2 for actual measurements). For Events 4 and 5, the pressure sensors were moved to the centre position of the pyramid test jig edge, giving standoff distances of approximately 445 mm and 465 mm, respectively (see Fig. 6 for pressure sensor positions). The peak pressure results are shown in Table 2 and Fig. 8. Superimposed on Fig. 8 is a graphical representation of the predicted pressure versus standoff distance equation by Cole.2 These results show that the pressure measurements correlated well with the theoretical equation by Cole,2 and therefore constituted valid pressure measurements.
Time measurements
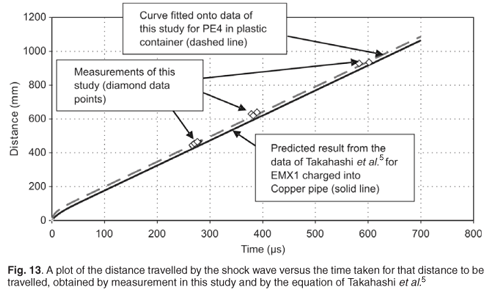
Figs 9–12 give the measurement results in scaled voltage. The point at time = 0 (on all graphs) is the point at which the measurement cycle, of duration 1 s, was initiated. The time topt is the time between the moment that the current through the detonator exceeded the explosion threshold (initiating the detonator) and the moment that the main charge flash was measured by the optical sensor. The time ts1 is the time between the flash detection by the optical sensor and the occurrence of the leading edge of the shock wave pressure measured by Sensor 1; and similarly the time ts2 is the time between the flash detection by the optical sensor and the occurrence of the leading edge of the shock wave pressure measured by Sensor 2. All four graphs are shown so that the differences between the measurements of Events 2–5 can be seen. The measured times (ts1 and ts2) are given in Table 3 and were plotted in Fig. 13 to show a visual correlation with the graphs obtained by Equation 4.
The optical sensor collector-emitter capacitance caused the negative slope to slew at a slower rate than the positive slope (see point A in Fig. 9 and Fig. 10). This effect was due to the fact that when the phototransistors were forward biased by the application of light, the forward resistance reduced to a relatively small value compared to the transistor capacitance. This relatively small forward resistance of the switched-on transistors appear in parallel with the collector-emitter capacitance. When the light caused by the explosion had expired, the forward resistance of the phototransistors increased to a value which was very high (practically causing an open circuit). The transistor capacitance then became the dominant part of the transistor impedance, which caused the voltage to drop at a slower rate than the rising slope of the measurement.
An additional 'slowing down' of the reactance of the phototransistor, may have been due to an avalanche effect (started at the presence of light which activated the photo characteristics of the transistor, but escalated to an oversaturation of light followed by a transistor avalanche) which should stop when the light disappears, but does not stop immediately. This characteristic varies between transistor types. The uncertainty of the switch-off time caused the measurement of a possible 'sustained light period' to be unreliable, but is not vital to this study and is therefore not discussed in more detail. The reason for the oscillations in the light-sensor measurements in Fig. 12 also is unknown, but does not affect our result.
Shock wave propagation velocity
The core aim of this study was to measure the velocity profile of the shock wave using the optical sensor leading edge output (explosion flash marker) as a reference point.
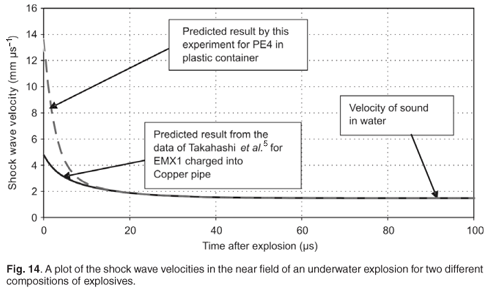
The actual times taken for the pressure shock wave to travel from the point of detonation (leading edge output of the optical sensor) to the pressure sensors were recorded as ts1 and ts2, shown in Table 3 and Figs 9–12. The distance–time results were transformed to velocity values (as described forthwith), and the results are shown in Fig. 14.
Distance–time results
Two published studies were found which have reported theoretical methods to calculate the distance–time curves and, by differentiation, the velocity history of the shock wave of an underwater explosion. These studies were by Kira et al.3 and Takahashi et al.;5 both measured the shock wave by streak photography, and then plotted the distance–time graph as it was captured by this photographic method. By using nonlinear curve-fitting methods, Kira et al.3 extracted an equation for R (Equation 4).
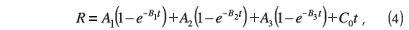
where R = standoff distance, C0 = sound velocity in the medium, and An and Bn = coefficients obtained by using nonlinear curve-fitting methods.
Takahashi et al.5 produced a similar equation. The coefficients An to Bn were called 'parameters' by Takahashi et al.,5 and it is presumed that they were influenced by the explosive formulation and explosive mass. From the graphical data supplied by Takahashi et al.,5 it was possible to extract the coefficient values of An and Bn in Equation 4. These coefficients are listed in Table 4. The first row in Table 4 refers to the experiment by Takahashi et al.,5 and the determination of the coefficients by curve-fitting methods. The second row in Table 4 refers to the results obtained by this study. The mass of the explosive material used by Takahashi et al.5 is not known, but, for the purposes of this study, a correlation was found between the shape of the curves produced in our study and by both Takahashi et al.5 and Kira et al.3 Kira et al.3 reported that the larger the diameter of the spherical explosives, the higher the initial velocity, resulting in higher end values of distance at the same time stamps.
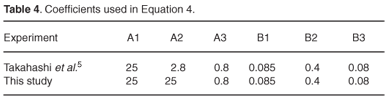
The distance–time curves in both Takahashi et al.5 and this study are shown graphically in Fig. 13. The points in Fig. 13 were the actual measurements obtained in this study, and the top curve (using Equation 4 and the coefficients shown in Table 4) was fitted onto the data points. The correlation coefficient between the data points and the fitted curve was 99.9%. The curve produced from the data by Takahashi et al.5 (bottom curve in Fig. 13) also corresponds well with the curve fitted (top curve in Fig. 13) onto the measured data points. This means that the measured data points represent a shock wave distance–time curve with a high degree of accuracy for the distances recorded by this experiment.
Shock wave velocity
The shock wave velocity can be calculated by differentiation of Equation 4, resulting in Equation 5:
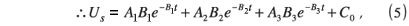
where Us = shock wave velocity, C0 = sound velocity in the medium, and An and Bn = coefficients obtained by using nonlinear curve-fitting methods.
The results of Takahashi et al.,5 as well as the results of this study, were combined in graphical format (after differentiation) in Fig. 14, which indicates that the shock wave velocity curves of two different explosive compositions and different encasings converged within 20 µs and approximated the speed of sound in water after about 40 µs. The validity of the curves in the time zone from 0 µs to 40 µs is not reported in this study, and is also not vital to this study; the data correlates well with the fitted curve due to the fact that they are linearly positioned on a linear portion of the theoretical Equation 4.
The optical sensor sustained no damage and laboratory tests before and after the sea trials were, within reason, identical (results not shown).
Conclusions and recommendations
This study was the first of a series of tests using an optical sensor to determine the point in time that could be used as a time marker for the moment of explosion in underwater explosions. This method proved to be reliable due to the rigidity of the sensor, the fast initial response time, the repeatability of the results, and the excellent correlation between the measured data and the theoretical data. We thus conclude that using the flash detection of an underwater explosion, by means of a optical sensor, as a marker for 'time zero' was successful in this study.
The secondary information gained from this experiment, the 'duration of the blast' (the 'sustained light period'), was deemed to not be reliable at this stage, because the phototransistors were overexposed, and displayed a characteristic of switching off relatively slowly (probably at an indeterminate time after the flash subsided). If the duration of this period were relevant, we suggest that a faster phototransistor or photodiode be used and calibrated against the standoff distance and amplification, such that saturation during the flash period would not occur.
1. Cooper P.W. (1996). Explosives Engineering, pp. 167–172. Wiley-VCH Inc., New York. [ Links ]
2. Cole R.H. (1948). Underwater Explosions, pp. 5–40. Dover Publications Inc., New York. [ Links ]
3. Kira A., Fujita M. and Itoh S. (1999). Underwater explosion of spherical explosives. J. Mater. Process. Technol. 85, 64–68. [ Links ]
4. Chung M. and Kinsey T. (1998). Investigation into the effects of underwater shock waves on simple structures, shielded and bare explosive materials. Technical Report: DSTO-RR-0134. DSTO Aeronautical and Maritime Research Laboratory, Melbourne. [ Links ]
5. Takahashi K., Murata K., Kato Y. and Itoh S. (1999). Non-ideal detonation of emulsion explosives. J. Mater. Process. Technol. 85, 52–55. [ Links ]
Received 7 April. Accepted 5 August 2009.
* Author for correspondence E-mail: aroux@csir.co.za














