Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.105 no.3-4 Pretoria Mar./Abr. 2009
RESEARCH ARTICLES
Singularity and symmetry analyses of mathematical models of epidemics
Dipartimento di Matematica e Informatica, Università di Perugia, 06123 Perugia, Italy
ABSTRACT
We present a summary of the methods of Lie symmetry and Painlevé singularity analyses and apply them to a number of well-known epidemiological models to demonstrate the utility of these analyses in the analysis of dynamical systems which arise during investigations of the evolution of diseases.
Key words: epidemiology, symmetry analysis, singularity analysis, mathematical modelling
1. Introduction
In the modelling of epidemics using systems of first-order ordinary differential equations, the traditional approach has been that of analysis from the viewpoint of dynamical systems. This is not surprising as most systems of differential equations are not integrable and so the qualitative description of the system offered by the theory of dynamical systems is regarded as better than no description at all. Indeed, when it comes to any analysis which is not numerical, the models of epidemiology—in common with similar fields such as ecology—have essentially been the preserve of dynamical systems, whereas in other areas of scientific endeavour, physics and engineering immediately come to mind, the more quantitative analyses due to Lie and Painlevé have become dominant in recent decades. This is not to gainsay the value of applications of the theory of dynamical systems in the more exact sciences, but it does seem curious that in the newer fields that are tending towards becoming exact sciences there has not been an adoption, let alone an enthusiastic adoption, of singularity and symmetry methods.
In this paper we seek to promote the use of singularity and symmetry analyses for epidemiological models as a standard routine. These analyses complement the results obtained through the methods of dynamical systems and consequently offer the prospect of providing greater information about the evolution in time of the system under consideration. In the two following sections we provide a brief outline of the methods of symmetry and singularity analyses so that this paper is complete in itself. The following section comprises a selection of examples treated in terms of the analyses of Lie and Painlevé which illustrate the methodology and at the same time illustrates some of the questions which can arise in terms of the analysis.
2. The elements of symmetry analysis
In January 2001, the first Whiteman prize for notable exposition on the history of mathematics was awarded to Thomas Hawkins by the American Mathematical Society. In the citation, published in the Notices of A.M.S. 48 (2001) 416–417, one reads that Thomas Hawkins ' has written extensively on the history of Lie groups. In particular he has traced their origins to [Lie's] work in the 1870s on differential equations the idée fixe guiding Lie's work was the development of a Galois theory of differential equations ... (Hawkins1) highlights the fascinating interaction of geometry, analysis, mathematical physics, algebra and topology '.
In the Introduction of his book2 Olver writes that 'it is impossible to overestimate the importance of Lie's contribution to modern science and mathematics. Nevertheless anyone who is already familiar with [it] is perhaps surprised to know that its original inspirational source was the field of differential equations'.
Lie's monumental work on transformation groups,3–5 and in particular contact transformations,6 has provided systematic techniques for obtaining exact solutions of differential equations.7 Many books have been dedicated to this subject and its generalisations.2,8–17
Lie group analysis is indeed the most powerful tool to find the general solution of ordinary differential equations. Any known integration technique can be shown to be a particular case of a general integration method based on the derivation of the continuous group of symmetries admitted by the differential equation, i.e. the Lie symmetry algebra.
The method developed by Lie is based on the use of infinitesimal transformations. Suppose that we have two variables, an independent variable denoted by t and a dependent variable denoted by x. An infinitesimal transformation in the variables, namely

where ε  1 is the infinitesimal parameter, is said to be generated by the differential operator
1 is the infinitesimal parameter, is said to be generated by the differential operator

i.e.

We call τ and ξ the coefficient functions.
An infinitesimal transformation in the variables t and x induces an infinitesimal transformation in any function of the two variables and their derivatives. The infinitesimal transformation for the first derivative is found as follows:
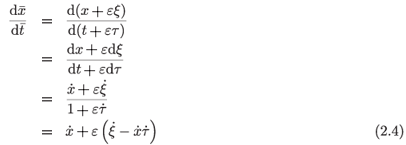
to the first order in the infinitesimal parameter ε. In a similar fashion the infinitesimal transformations for derivatives of higher orders may be calculated.
Thus we have

etc.
Naturally, these considerations may be extended to several dependent and several independent variables. As we are concerned with ordinary differential equations in this paper, we mention that the variation in (2.4) and (2.5) for several dependent variables is to include suitable subscripts on x and ξ.
To deal with the infinitesimal transformations induced in derivatives by the infinitesimal transformations in the original variables in terms of the generator Γ, we extend the generator to

to deal with the first derivative,  , to
, to

to deal with the second derivative, 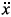 , and in general to
, and in general to
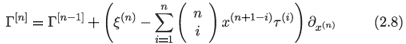
to deal with the nth derivative, x(n)
The generator, Γ, is a symmetry of a function, f(t,x, ,...,x(n)), if
,...,x(n)), if

The generator is a symmetry of a differential equation, f(t,x, ,...,x(n)) = 0, if
,...,x(n)) = 0, if

i.e. the constraint of the differential equation is taken into account in the computation. The equation resulting from the application of the nth extension of Γ, (2.9) in the case of a function and (2.10) in the case of an equation, is called the determining equation.
We have not remarked on the functional dependence of the coefficient functions, τ and ξ. Lie was motivated by geometric considerations when he introduced the idea of the application of infinitesimal transformations to differential equations. Consequently, the infinitesimal transformations were geometrically correct. Initially, he used point transformations in which the coefficient functions were simply functions of the independent and dependent variables. Subsequently, Lie made use of contact transformations in which the coefficient functions could depend on the first derivative in such a way that the first extension was independent of the second derivative. When Noether published her seminal paper on the invariance of the Action Integral under infinitesimal transformations,17 she employed generalised transformations depending on derivatives of all orders without any constraint such as that which is found with a contact transformation. In the last two decades a more general type of transformation, nonlocal, in which the coefficient functions can depend on integrals as well as derivatives, have had of necessity to be considered since without them the concept of the relationship between the existence of symmetry and integrability presented some difficulties. In terms of applications the point and contact symmetries are the easiest to use, with the former being computationally simpler than the latter. In the case that a function or differential equation admits more than one symmetry, the algebraic properties of these types of symmetry are easy to handle. Generalised symmetries are more commonly used in analyses of partial differential equations than of ordinary differential equations, even including Noether's Theorem, although it was originally stated in terms of generalised symmetries. There still remain some questions to be resolved about nonlocal symmetries,18 but there can be no question about the necessity for their existence and utilisation, although in certain circumstances19–21 they can be local in disguise.
The computation of symmetries requires the solution of the determining equation or equations. We noted above that (2.9), respectively (2.10), was the determining equation for the symmetries of a function, respectively differential equation. In the calculation of a nonlocal symmetry that is the only equation to be solved. In the case of point, contact and generalised symmetries, the Ansatz made about the functional dependence of the coefficient functions leads to a partial separation of the determining equation into a set of determining equations. For example, in the calculation of the point symmetries of a scalar second order ordinary differential equation one would separate by coefficient of powers of the first derivative and typically there would be four linear partial differential equations to be solved for the coefficient functions and as such the underdetermined single equation becomes an overdetermined system. The calculation of symmetries for anything apart from the simplest of differential equations is a tedious business fraught with the likelihood of error. Fortunately, there is an algorithmic nature to the calculations which lends itself to implementation using one of the symbolic manipulation codes.22–25 A list of the codes then available was presented by Hereman.26,27
The typical mathematical models found in epidemiology are systems of first-order ordinary differential equations and this presents a problem in terms of the calculation of Lie symmetries, no matter what the subvariety. Any system of first-order ordinary differential equations possesses an infinite number of Lie symmetries. For a practical resolution of the problem there are two approaches possible. In one of them an Ansatz is made of the structure of the coefficient functions. Although this approach is open to the fundamental objection that the Ansatz is more likely to be based on the imagination of the person making the analysis than of the inherent features of the system under consideration, there have been occasions when this is a very fruitful approach. In the second approach the method of reduction of order20,28,29 effectively replaces a first-order system by one containing at least one second-order equation which reduces the number of symmetries from infinity to a finite number, which one hopes is not zero. Then the system, not the imagination of the investigator, determines the symmetries. Nucci20 has remarked that a system of n first-order equations could be transformed into an equivalent system where at least one of the equations is of second order. Then, the admitted Lie symmetry algebra is no longer infinitely dimensional, and nontrivial symmetries of the original system can be retrieved.20 This idea has been successfully applied in several instances.20,21,30,31 Also, Marcelli and Nucci32 have shown that first integrals can be obtained by Lie group analysis even if the system under study does not come from a variational problem, i.e. we can find first integrals without making use of Noether's Theorem.17 If we consider a system of first-order equations and, by eliminating one of the dependent variables, derive an equivalent system which has one equation of second order, then Lie group analysis applied to that equivalent system yields the first integral(s) of the original system which do(es) not contain the eliminated dependent variable in the case that such first integrals exist. The procedure should be repeated as many times as there are dependent variables in order to find all such first integrals. The first integrals correspond to the characteristic curves of determining equations of parabolic type which are constructed by the method of Lie group analysis. We would like to remark that interactive (not automatic) programs for calculating Lie point symmetries, such as that of Nucci,22,23 are more appropriate for performing this task.
We illustrate some aspects of the Lie method and the devices mentioned above with the simple two-dimensional system

where we have included a parameter a to be able to add some additional detail to the illustration.
As we remarked above, the problem, as far as symmetries are concerned, with systems of first-order equations is that they have an infinite number of point symmetries and there does not exist a closed-form algorithm for their determination. It is obvious that the system possesses the two symmetries

where Γ1 reflects the autonomy of the system and Γ2 the invariance of the system under a self-similar transformation.
We obviate the necessity to deal with the infinite by converting the two-dimensional system of first-order equations to a single second-order equation.
From (2.11) we have

We use (2.14) to eliminate the variable y from (2.12) and obtain the second-order equation

Equation (2.15) can be analysed for its Lie point symmetries by means of a hand calculation. Even though (2.15) is a fairly simple equation, the calculation is by no means trivial. When we use the interactive code of Nucci,22,23 we find that for general values of a there are just the two Lie point symmetries given above in (2.13) without the presence of the variable y. However, for the particular value of a = 3 which is prompted by the code, i.e. for the equation

we obtain the eight symmetries

with the Lie algebra sl(3, R).33,34 This means that Equation (2.16) is linearisable by means of a point transformation.7 In order to find the linearising transformation we have to look for a two-dimensional abelian intransitive subalgebra and, following Lie's classification of two-dimensional algebras in the real plane,7 we have to transform it into the canonical form

with  and
and 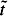 the new dependent and independent variables, respectively. We find that one such subalgebra is that generated by Γ1 and Γ4 – 2Γ6, which yields the following point transformation
the new dependent and independent variables, respectively. We find that one such subalgebra is that generated by Γ1 and Γ4 – 2Γ6, which yields the following point transformation

and Equation (2.16) becomes

the solution of which, hence that of (2.16), is trivial. For general values of the parameter, a, (2.15) is integrable in the sense of Lie. A detailed study was performed by Lemmer and Leach.35
3. Singularity analysis
Singularity analysis was initiated by Kowalevski36 in her determination of the third integrable case of the Euler equations for the top and was in large measure developed by the French School developed by Paul Painlevé about the period of La Belle Époque.37–40 There have been significant contributions since then. For a recent and an erudite contribution to the state of the art see the book edited by Conte.41 For less technical works devoted to the methodology the interested reader is referred to the text of Tabor42 and the report of Ramani et al.43 The essence of the singularity analysis of a differential equation (æq system of ordinary differential equations) is the determination of the existence of isolated movable polelike singularities about which one can develop a Laurent expansion containing arbitrary constants equal in number to the order of the system. The location of the singularity is determined by the initial conditions of the system. An equation of moderately, or more, complicated structure can possess more than one polelike singularity—a fortiori in the case of systems of differential equations which can have many patterns of singularities—and it is conventional wisdom that a Laurent expansion with the requisite number of arbitrary constants must exist for all possibilities. However, there exists a counter-example44 for which one pattern of singular behaviour possesses a Laurent expansion with the correct number of arbitrary constants and the second does not, but has a 'peculiar' solution45 of the type already discussed by Ince46, p. 355 many years ago. Nevertheless, the closed form general solution of the system is manifestly analytic.
The application of the analysis is usually quite algorithmic. Indeed, it is standard practice to apply the ARS algorithm,47–49 although there are instances, of particular relevance to the analysis of systems of first-order ordinary linear differential equations typically encountered in the mathematical modelling of epidemics, in which the subtler approach advocated by Hua et al.50 is to be preferred. First, we outline the standard algorithm and secondly the alternative approach. Consider an autonomous system of first-order ordinary differential equations

where x represents the n dependent variables, the overdot differentiation with respect to the independent variable t and σ the set of parameters which invariably seems to accompany a system arising in the course of the mathematical modelling of natural phenomena. We assume that the n functions Φi are polynomials in the dependent variables x and linear in the first derivatives. The assumptions which we make are not completely necessary, but they do reflect the reality found in models and simplify our theoretical discussion.
By writing the system as we have in (3.21) we include models in which, say the variable population N appears in the denominator of a fraction. The analysis may be extended to time-dependent parameters provided that they are analytic functions of the time.
The first step is to determine the leading-order behaviour of the dependent variables of the system. We substitute  i = 1, n, where τ = t – t0 and t0 is the putative location of the movable singularity, into the system (3.21) and compare the resulting powers. For example, if we take the elementary system
i = 1, n, where τ = t – t0 and t0 is the putative location of the movable singularity, into the system (3.21) and compare the resulting powers. For example, if we take the elementary system

the powers to be compared are

for the two equations, respectively. All terms balance if p = q = –1. This is stated as all terms are dominant. It is reflected in the existence of a self-similar symmetry, Γ = ∂t + x∂x + y∂y, for the system. It is a general feature of the singularity analysis that the dominant terms share the same self-similar symmetry. If we had included some linear terms, these would not share the same self-similar symmetry and would not be dominant. Consequently, they would not enter into the determination of the coefficients of the leading-order terms. In this elementary example the analysis of the leading-order behaviour indicates that there is a singularity and that it is a simple pole. The coefficients of the leading-order terms, α and β, are determined by the solution of the linear system

when the values of p and q are taken into account.
There are two possibilities for the system (3.24). The first is that the coefficient matrix be singular. In this case for the system to be consistent the augmented matrix must also be of rank one. The former requires that ab = 1. The latter increases the requirement to a = b = 1. If this be the case, the system (3.22) satisfies the requirements of the analysis since the second arbitrary constant enters the Laurent expansion at the leading-order term. Hence the system is integrable and is said to possess the Painlevé Property.
The second possibility is that the coefficient matrix is regular. We solve (3.24) to obtain the leading-order coefficients as

In the case that the leading-order behaviour does not provide the correct number of arbitrary constants—the generic situation illustrated by the results given in (3.25)—it is necessary to determine whether there exists a term, or terms, at which the requisite number of arbitrary constants can enter. The powers at which these arbitrary constants enter are almost always called resonances—on occasion they are also known as Kowalevski exponents (after the pioneering woman in this area). To determine the resonances one makes the substitution

into those terms of the system (3.21) which have been identified as dominant for the set of values pi, i = 1, n, and the associated coefficients αi already determined. The terms linear in the constants µi are required to be zero. This leads to an eigenvalue equation for the exponent r and the solution of this equation provides the resonances.
We return to our example to illustrate how the determination of the resonances proceeds. We substitute

into the system (3.22)—recall that all terms are dominant in this example—and collect the terms linear in µ and ν to obtain the system of equations
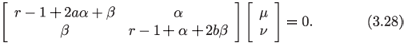
The requirement that the system be consistent leads to the equation

after the explicit expressions for α andβ have been substituted from (3.25).
The solution of (3.29) is just

The first value, –1, is always present (its absence indicates that a computational error has occurred). In systems of equations it may even occur as a multiple root and thus put paid to any possibility that the system can possess the Painlevé Property,51 although Andriopoulos and Leach52 have convincingly demonstrated that the loss is not automatic. The serious root is the second. For a system to possess the Painlevé Property this root must be an integer. If it be a positive integer, the Laurent expansion is known as a Right Painlevé Series since the exponents commence at –1 and increase to a presumed infinity. If it be a negative integer, the Laurent expansion is known as a Left Painlevé Series since the exponents commence at a presumed minus infinity and increase to –1. The Left Painlevé Series was recognised considerably later than the Right Series.35,53 In the case that the nongeneric resonance is a rational number the expansion can be made in terms of fractional powers—the same be true if the exponent of the leading-order behaviour be rational. In this case the solution cannot be analytic. Rather, it has a branch point singularity. Provided the denominator of the fractional power is not great, the expansion is acceptable. If the dominator is large, the complex plane is divided by so many branch cuts as to be effectively useless for the almost inevitable numerical computations used in the solution. When fractional powers are included in the expansion, the system is said to possess the weak Painlevé Property.
After the leading-order behaviour and resonances have been determined to be satisfactory, there is usually the necessity to check for consistency. If not all of the terms in the system of equations are dominant and there are nonzero resonances, a substitution of a polynomial to the greatest resonance into the full system is required to ensure that the presence of the nondominant terms does not lead to inconsistency. A system which is a candidate for an expansion in terms of a Left Painlevé Series cannot have nondominant terms. The reason for this is that the Left Painlevé Series represents a Laurent expansion on the exterior of a disc centred on the singularity. The leading-order term then represents the asymptotic behaviour of the solution. A nondominant term would be less singular and so there is an inherent contradiction. In the case of multiple nonzero resonances it is always necessary to check that an arbitrary constant introduced at one resonance is not constrained to take a particular value at the next resonance. There is always the possibility that some of the nongeneric resonances will be positive and others negative. This has led to some confused thinking until Andrioupoulos and Leach54 showed that the Laurent expansion occurred over an annulus in which the leading-order terms could dominate both the ascending powers and the descending powers. Hence, even if everything be otherwise consistent, an expansion in just one direction cannot be a representation of the general solution. It could, however, represent a 'peculiar' solution45 of the type already recognised by Ince45, p. 46. For such a solution there is no question of adding a logarithmic term as is the case when there is an inconsistency at a resonance. Naturally, the addition of a logarithmic term means that the solution cannot be analytic.
We return to our example and the expression for the nongeneric resonance given in (3.30). We require this to be an integer for the system to possess the Painlevé Property. Equally we could consider the possibility of the possession of the weak Painlevé Property, but for purposes of the discussion of the application of the Painlevé Test we confine our attention to integral values. Since all terms are dominant, the admissible values of the nongeneric resonance are not confined to positive integers. They can also be negative integers. This is a rather unusual situation. All that is required is that the parameters a and b be related according to

where n ∈ Z. Thus for our example system to be integrable in the sense of Painlevé it is necessary for there to be a constraint on the parameters of the system. This is a very typical result. Integrability is not guaranteed for all possible values of the parameters, but only for a restricted set. In the case of our example integrability of the system (3.22) occurs only on the curves in the two-dimensional space of parameters specified by Equation (3.31).
The second approach to the determination of the resonances and question of consistency mentioned above50 does not separate the two processes. This approach is particularly suited to a system containing a selection of parameters. Typically such systems are only integrable subject to some constraint(s) on the parameters. After the nature of the polelike singularity is identified, the series

is substituted into (3.21) if a Right Painlevé Series is indicated and

if a Left Painlevé Series is indicated. The coefficients at each power are collected to give a set of equations linear in the coefficients introduced at that power (for j > 0; for j = 0 the equations need not be linear in the coefficients of the leading-order terms). These equations are solved successively for increasing values of j with the possibility of branching—existence of a resonance or not—being determined. In the branch for which a resonance could be, the constraints upon the parameters are determined simultaneously.
We revert to our example, the simple system (3.22). The examination for leading-order behaviour has given a simple polelike singularity. We then substitute

to obtain

We illustrate the workings of the algorithm with the first few powers.

One could imagine a rather strange-looking solution if the resonance did not occur for a fairly low power. For in a system such as this in which all terms are dominant the effective power of the expansion is determined by the value of the resonance. For example, in the simple equation of Emden-Fowler type,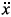 = x2, the leading-order behaviour is 6τ–2 and the nongeneric resonance is 6. This means that the Laurent expansion is of the form
= x2, the leading-order behaviour is 6τ–2 and the nongeneric resonance is 6. This means that the Laurent expansion is of the form 
A similar series of calculations occurs in the case of possible existence of a Left Painlevé Series.
4. Illustrative examples
We consider some examples of models which arise in mathematical epidemiology in terms of singularity and symmetry analyses. In these examples we wish not only to illustrate the application of the methods introduced above in terms of success stories but also to highlight some of the difficulties and problems which occur in these analyses.
A SIR model
In 1927 Kermack and McKendrick55 introduced their famous SIR model of the Great Plague of London in 1665–1666. They used a system of three first-order ordinary differential equations, namely

in which S represents that portion of the population which is susceptible to the disease, I that portion of the population which is infected by the disease, and R that portion of population which is removed from the population due to the disease. The susceptibles succumb at a rate proportional to the degree of interaction between susceptibles and infectives. The characteristic timescale of the disease is such that standard methods of entering and leaving the population may be ignored. Since the variable R is consequent upon the other two variables, we may ignore (4.39) and perform our analyses on (4.37) and (4.38).
To determine the leading-order behaviour we set

and substitute these into (4.37) and (4.38) to obtain

The balancing of powers is between the terms arising from the derivative and the nonlinear term in each equation. Quite obviously
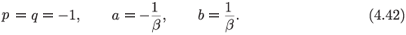
We find the resonances from the substitution
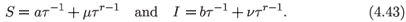
They are r = ±1 and ν = –µ. When we substitute (4.43) into the full system, we find that there is an incompatibility unless α = 0. This indicates that no one is removed from the class of infectives and suggests that the disease is more in the nature of a lingering illness and so the neglect of natural additions and removals is invalid. Consequently, the connection with the Great Plague becomes vanishingly tenuous.
For the sake of completeness we consider the symmetry aspects. This is, as we noted in our general discussion above, better done at an order other than the first. We eliminate I to obtain the second-order ordinary differential equation

for S. We note that the Painlevé Test fails with (4.44) for the same reason as it did for the system of two first-order equations. There is not necessarily a one-to-one correspondence between passing the Painlevé Test by a system of first-order equations and an 'equivalent' higher-order equation.44
With α = 0, (4.44) passes the Painlevé Test. A standard method for treating a nonlinear equation such as (4.44) is to raise it to a higher order by means of a Riccati transformation.19 With α = 0 we obtain a generalised Kummer-Schwarz equation, namely

and we note the appearance of the same factor, namely 1/β, as appeared in the Painlevé analysis. The original second-order equation, namely (4.44) with α = 0, is integrable in the sense of Lie since it possesses the two obvious Lie point symmetries, namely ∂t and t∂t + S∂S. In increasing its order to the third we find four Lie point symmetries in (4.45), namely ∂t, t∂t, ∂w and w∂w. The third of these is unexpected57 and arises since the symmetry associated with the Riccati transformation is not the normal subgroup of the two symmetries ∂w and w∂w. When one reduces (4.45) to (4.44) using w∂w,∂w ceases to be a point symmetry. Rather it becomes the exponential nonlocal symmetry56 S exp[βSdt]∂S and so ∂w is a Type I hidden symmetry.58,59 We use ∂w to reduce (4.45) to the linear second-order equation

Equation (4.46) has eight Lie point symmetries with the Lie algebra sl(3, IR). The important point to note is that the integrable case of (4.37)–(4.39) according to the singularity analysis could be reduced to a linear equation. This is not an uncommon observation.
Brauer60 offers a more elaborate model than (4.37)–(4.39) which allows for a constant rate of population growth, death by natural other—not related to the disease under consideration—causes and the possibility of recovering from the disease with immunity. The model equations are

where the dependent variables S, I and R and the parameters α and β have the same meanings as in (4.37)–(4.39) . The constant rate of population growth is µK, the rate of recovery from the illness with immunity conferred is governed by γ, and µ represents the death rate from other causes. This last is assumed to be the same for the three components of the population. As in the case of (4.37)–(4.39) the third member of this system may be omitted from the analysis. The analysis is virtually identical to that of the system (4.37)–(4.39). We find that the system (4.47) and (4.48) is integrable in the sense of Painlevé provided α + γ = 0. The effect of α + γ = 0 is more easily seen if we take

Then the system (4.47)–(4.49) can be replaced with the system
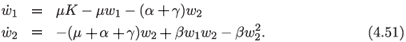
When α + γ = 0, the system decouples to

Equation (4.52) is trivially integrable in terms of an exponential function, which is analytic. With this solution (4.53) becomes a Riccati equation. With the Riccati transformation, w2 = 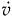 /(β)v , the Riccati equation becomes a linear first-order equation in
/(β)v , the Riccati equation becomes a linear first-order equation in 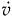 and is integrable in terms of analytic functions. Since both α and γ are essentially nonnegative, it appears that the needs of the singularity analysis are satisfied if none of the infectives dies from the disease and none of the infectives recovers with immunity against reinfection.
and is integrable in terms of analytic functions. Since both α and γ are essentially nonnegative, it appears that the needs of the singularity analysis are satisfied if none of the infectives dies from the disease and none of the infectives recovers with immunity against reinfection.
A model for the transmission of HIV
A model61 which has been quite successful30 in replicating results reported in studies of HIV transmission in the San Francisco area is62–64
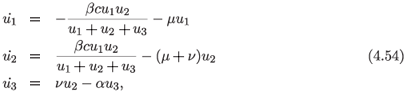
where u1(t) represents that part of the population which is HIV negative, u2(t) that part of the population which is HIV positive, and u3(t) that part of the population which has AIDS. The parameter µ is the death rate from other causes, α the death rate from AIDS and ν the rate at which HIV positives develop AIDS. The parameters β and c represents the rates of infection and of change of partner, respectively.
It is obvious from direct inspection of the system (4.54) that it cannot possess the Painlevé Property since there can be no balancing of leading-order terms. It is also obvious that there are two Lie point symmetries, namely

Indeed, it is the very possession of Γ2, representing the homogeneity of the system (4.54) in the dependent variables, which precludes the possibility of the system possessing the Painlevé Property. This is in contrast to a system which, in addition to possessing the symmetries Γ1 and Γ2, also possesses the symmetry t∂t which represents the homogeneity in the independent variable. Then such a system may possibly possess the Painlevé Property.65 These two point symmetries are insufficient for integrability. We know that a system of first-order ordinary differential equations possesses an infinite number of Lie symmetries.
We need but one of these to constitute a three-dimensional solvable Lie algebra for then we can reduce the integration of the system (4.54) to quadratures. Apart from obvious symmetries, such as the two given in (4.55), the only way to analyse the system (4.54) for symmetries is to make some Ansatz for the structure of the coefficient functions of the symmetry. This is not a completely satisfactory procedure since the Ansatz is more likely to be determined by the imagination of the searcher than the internal structure of the system being investigated. An alternative procedure20 is to transform the given system, (4.54), to an equivalent system containing an higher-order equations. In the case of a system of three first-order equations there are two options. The first is a system of one second-order and one first-order equation. The second is a scalar third-order equation. We choose the first option. The Lie algebra of point symmetries admitted by this system is now finite-dimensional and the determination of the symmetries can be performed using Lie's method. The system, obtained by the elimination of u3 from (4.54a), contains many terms and the Lie analysis is best performed using a package for the determination of symmetries.22,23 Torrisi and Nucci30 found that in the case α = µ+ βc that the system was linearisable and separable. Of the additional symmetries, the symmetry
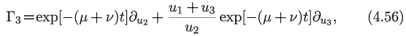
expressed in terms of the original variables, provided the required solvable algebra. In view of our comments above about the lack of possession of the Painlevé Property it comes as no surprise that the solution is manifestly nonanalytic. Torrisi and Nucci30 found that the explicit solution to the system (4.54) is

If βc = 2ν, the general solution assumes the simpler form:

Tuberculosis with fast and slow dynamics
In a paper modelling the transmission dynamics of tuberculosis, Song66 uses two modes for routes of infection, namely close contacts in quasipermanent 'households' and casual contacts in the general population. This leads naturally to a consideration of differential timescales. A consequence of this is that the original system of five first-order equations can be split into two classes, those on the fast manifold and those on the slow manifold. By making an Ansatz that the fast variables reach a quasisteady state while the slow variables are still evolving in their own time, the system of equations modelling the slow variables may be written as

where x1 and x2 are rescaled variables representing susceptible and latently-infected individuals not belonging to a 'household', Q is the expected number of infections produced by one infectious individual and B = µ/k, with µ being the natural mortality rate and k the per capita progression rate.
When we rewrite the system (4.63) as

it is quite obvious that the system cannot possess the Painlevé Property. We can rewrite the system as a single second-order ordinary differential equation in the variable u = x1 + x2, which is strongly suggested by the structure of (4.64), namely

This equation does not possess any singular leading-order behaviour and so cannot possess the Painlevé Property except in the trivial sense. We use the standard stratagem

for introducing the possibility of singular behaviour and obtain the equation

We find the leading-order behaviour –(Bτ)–1, where τ = t – t0. In the calculation of the resonances the parameters B and Q disappear. Unfortunately, one finds that r = 1, 0, i.e. the second arbitrary constant must enter at the power τ–1. This means that a logarithmic term must be introduced and so any hope of an analytic solution is lost.
When we analyse (4.65) for Lie point symmetries apart from the obvious ∂t, we find that there exists a second symmetry under a variety of relationships between B and Q. All of them are special cases of Q = B + 1. When this constraint applies, we have the two Lie point symmetries

The second symmetry has a remarkable resemblance to the additional symmetry found by Torrisi and Nucci30 reported in (4.56) when an additional constraint was imposed on the parameters of the model for the equation
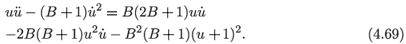
Since the Lie Bracket, [ Γ2, Γ2] = –BΓ2, and Γ1  ρ(t, u)Γ2, this equation is of Lie's Type 3.7, Kap 18 The equation (4.69) is transformed to the standard form
ρ(t, u)Γ2, this equation is of Lie's Type 3.7, Kap 18 The equation (4.69) is transformed to the standard form

by the point transformation

Equation (4.70) is easily integrated once to

but, perhaps not surprisingly, further progress to the solution is not obvious.
We note that trivially in the case that Q = 0 Equation (4.65) is linear and has eight Lie point symmetries, but this is not a realistic paradigm.
Another approach is to reduce the original system to a first-order equation by eliminating the independent variable. We divide (4.64a) by (4.64b) to obtain
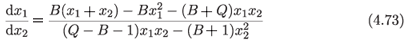
and observe that, under the constraint Q = B + 1 encountered above for the existence of an additional Lie point symmetry of the equivalent second-order system, this equation reduces to the Riccati equation

Equation (4.74) is converted to the linear second-order equation

where the prime denotes differentiation with respect to the new independent variable x2, by means of the Riccati transformation

and to the confluent hypergeometric equation

by means of the transformation67

A connection with linearity has been established for Q = B + 1. Note that we have x1 as an analytic function of x2 except for isolated singularities. One can obtain the general solution x1(x2) using the package MAPLE 7. The expression is somewhat complex and we do not write it here. For general values of the parameter B the solution is expressed in terms of Whittaker functions. Simpler solutions are found for specific values of B, for example, when B =  , the solution is given in terms of a combination of Gamma and circular functions. For specific values of the initial conditions and a given value of the parameter B the solution produced by MAPLE 7 can be used to plot the phase portrait.
, the solution is given in terms of a combination of Gamma and circular functions. For specific values of the initial conditions and a given value of the parameter B the solution produced by MAPLE 7 can be used to plot the phase portrait.
Since (4.74) is a Riccati equation, it possesses the Painlevé Property, i.e. x1 is an analytic function of x2 away from the movable simple pole. Thus we have the rather curious situation that the dependent variables are related analytically to each other, but do not have an analytic dependence upon the independent variable.
The impact of a disease on demographic growth
Song et al. 68 discuss the global dynamics of tuberculosis models in which the demography is taken to be density-dependent. Their model reduces to the two-dimensional system

in rescaled variables. It is important to know how the parameters A1, A2 and A3 relate to the physical parameters lest one make a claim of integrability for physically unacceptable values. We have
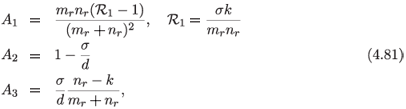
where mr = b0 + ρ + d, nr = b0 + α + k and b0 is the parameter of the recruitment rate, b0N, d is the tuberculosis-induced mortality rate, k is the per capita rate of progression from active tuberculosis to latent tuberculosis, α and ρ denote the treatment rates for the latent and infectious cases respectively and σ = βc, the product of the average infected proportion of susceptibles, β, and the per capita contact rate, c. A1 may be positive or negative, A2 is bounded above by 1 whereas A3 is always positive.
The exponents for the usual leading-order behaviour substitution, x = ατp and y = βτq are

from which it is evident that there are two possible patterns of singularity behaviour, namely p = q = –1, which contains the left-hand side and the third term of the right-hand side of (4.79) and the left-hand side and the second and third terms of the right-hand side of (4.80) as dominant terms, and p = –1, q = –2, which contains the left-hand side and the second and third terms of the right-hand side of (4.79) and the left-hand side and the third term of the right-hand side of (4.80) as dominant terms.
We analyse each in turn.
p = q = –1:
The coefficients of the leading-order terms are

and we recall that A2 < 1. The eigenvalue problem for the resonances is
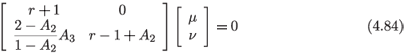
with the solution r = –1, 1 – A2. We note that at the nongeneric resonance the eigenvector is (0,1)Tν, where ν is arbitrary. From (4.81) the nongeneric resonance is just σ/d, i.e. one requires that the parameters β, c and d be related according to

This is not impossible.
p = –1, q = –2:
In this case the coefficients of the leading-order terms are

The eigenvalue problem for the resonances is

with the solution r = –1, –2(2 – A2)/A2. The eigenvector for the latter, non-generic, resonance is (1, 1)Tµ, where µ is arbitrary. In this case the constraint on the parameters β, c and d is
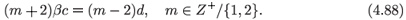
Given that d is usually small the satisfaction of (4.88) is not as likely as that of (4.85) in most populations.68, p. 278
For each item of singularity behaviour there exist families of values of the parameters—interestingly, only b, c and d are involved in the behaviour of the dominant terms—for which the first two requirements of the singularity analysis are satisfied. However, unless one can explicitly prove to the contrary (cf. the explicit demonstration by Leach and Nucci44), both patterns of singularity behaviour are required to satisfy the conditions of the Test. This means that both (4.85) and (4.88) must hold, i.e. n =(m – 2)/(m + 2), which is not going to be satisfied by integral m and n. Of course we can always relax the analysis to that of the testing for the possession of the weak Painlevé Property.
We allow m and n to be rational and consider the system (4.79)–(4.80) as a candidate for the position of the weak Painlevé Property.
We must now consider the consistency of the expansion, which is satisfactory for the dominant terms, with the complete system. We first consider the second pattern of singularity behaviour. The nongeneric resonance must be negative for a physically feasible set of parameters. This negativity, suggestive of a Left Painlevé Series, is inconsistent with the presence of nondominant terms no matter the rationality or wholeness of the nongeneric resonance. The (weak) Painlevé Property cannot be possessed for this pattern of singularity behaviour.
There is then no point in examining the other item of singularity behaviour even though as a candidate for a Right Painlevé Series the presence of nondominant terms does not present a priori any difficulty. However, in case this is one of those systems44 which fails the Painlevé Test for one of the singular patterns but yet which is integrable in terms of analytic functions we should examine the system from a different viewpoint.
One approach is to replace the two-dimensional system of first-order equations with a single second-order equation. From (4.79)

and, when this is substituted into (4.80), we obtain the nonlinear second-order equation

It is evident that the first three terms are dominant and that the exponent of the leading-order terms is –1. The coeffcient is a solution of

The eigenvalue equation for the resonances is
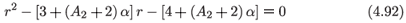
whence

Since σ > d, both values for the nongeneric resonance can be positive integers, although the number of possible values is limited.
By way of example we take A2 = –2, i.e. σ = 3d. Then α = ±1 and the nongeneric resonance is 4 in both cases. We substitute

into (4.90) to check for consistency at the resonance. The relationship to be satisfied that each power of τ is
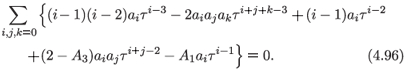
We equate the coefficients of successive powers of τ to obtain the coefficients

At τ1 a4 is arbitrary by construction and the consistency condition is the constraint

We back-substitute from (4.97) into (4.98). When the expression in simplified, there is a part independent of a0 and a part linearly dependent on a0. Since a0 takes the values ±1, both parts must separately be zero. From these we obtain

where A3 is constrained by the equation

There is only one real root of (4.100). Equation (4.90) possesses the Painlevé Property for the set of parameter values

This set of values is not unrealistic in that the value of A2 gives σ = 3d, which is certainly in the right direction, and A1 < 0 is a regime in which the proportion of infectives in the total population approaches zero as time increases68 and could be regarded as somewhat cheering.
The other suitable choices of A2 can be similarly treated.
Thus under constraints on the parameters the second-order equation (4.90) is integrable in the sense of Painlevé and we can conclude that so also is the two-dimensional system of first-order equations, (4.79) and (4.80), since the transformation (4.89) is of the type which preserves the Painlevé Property.44
If we analyse (4.90) for the existence of Lie point symmetries with the value A2 = –2 chosen above for the purposes of illustration using the interactive code of Nucci,22,23 we find that for general values of A1 and A3 there is just the obvious single symmetry ∂t. However, in the process of the interactive analysis branching occurs which separates the values A1 = –2/9 and A3 = 2. For the values of the parameters (4.90) has the two Lie point symmetries

The symmetry Γ2 has something of the nature of a rescaling symmetry. Similar symmetries have been observed in other integrable systems.30,69 The method for the integration of the equation under consideration, namely

without a knowledge of the Lie point symmetries is not obvious. Using the classification of two-dimensional Lie algebras in the real plane,7 we introduce the canonical variables ψ = exp(–t/3) (9 + 1/x), ø = exp(–t/3)/x) which transform Equation (4.103) into the canonical form

This equation can be easily solved in terms of elliptic functions by Maple to give:

where c1 and c2 are arbitrary constants. Finally the general solution of (4.103) is

where JacobiSN denotes the Jacobi elliptic function, sn.
Comments and conclusion
In this paper we have outlined the methods of symmetry and singularity analyses with specific reference to the types of systems of first-order equations found in compartmental models arising in epidemiology and illustrated the working of the methods on some specific examples found in the recent literature.
The results obtained are fairly typical of what one would expect in that the demands of integrability generally impose constraints upon the parameters of the model.
Everyone knows that integrable systems are a rarity. It may be that so many of the nonlinear systems which arise in epidemiology and related areas are nonintegrable that practitioners in this field have been dissuaded from using the methods of integrable systems in favour of the qualitative methods of dynamical systems. This is quite understandable. However, there seems to have developed a reluctance to use exact methods as a consequence. We have sought to promote the use of Lie and Painlevé analyses for mathematical models in epidemiology and more generally in the biosciences as a standard routine. What we hope to have shown in this paper is that, even in the case of nonintegrable systems, exact methods can yield a great deal of information. These analyses complement the results obtained through the methods of dynamical systems and consequently offer the prospect of providing better insight about the evolution in time of the system under consideration.
P.G.L.L. thanks the Università di Perugia and M.C. Nucci for their kind hospitality during the period in which this work was performed, and the University of KwaZulu-Natal and the National Research Foundation of South Africa for their continuing support. The work reported in this paper is part of a project funded under the auspices of the 2001 Italian-South African Scientific Agreement in Medicine and Health.
1. Hawkins T. (2002). The Emergence of the Theory of Lie Groups: An Essay in the History of Mathematics 1869–1926. Springer–Verlag, New York. [ Links ]
2. Olver P.J. (1993). Applications of Lie Groups to Differential Equations. Springer-Verlag, New York. [ Links ]
3. Lie S. (1888). Theorie der Transformationsgruppen. Erster Abschnitt. B.G. Teubner, Leipzig. [ Links ]
4. Lie S. (1890). Theorie der Transformationsgruppen. Zweiter Abschnitt. B.G. Teubner, Leipzig. [ Links ]
5. Lie S. (1893). Theorie der Transformationsgruppen. Dritter und Letzter Abschnitt. B.G. Teubner, Leipzig. [ Links ]
6. Lie S. (1896). Geometrie der Berührungstransformationen. B.G. Teubner, Leipzig. [ Links ]
7. Lie S. (1912). Vorlesungen über Differentialgleichungen mit Bekannten Infinitesimalen Transformationen. B.G. Teubner, Leipzig. [ Links ]
8. Bluman G.W. and Cole J.D. (1974). Similarity Methods for Differential Equations. Springer-Verlag, New York. [ Links ]
9. Ovsiannikov L.V. (1982). Group Analysis of Differential Equations. Academic Press, New York. [ Links ]
10. Bluman G.W. and Kumei S. (1989). Symmetries and Differential Equations. Springer-Verlag, New York. [ Links ]
11. Stephani H. (1989). Differential Equations. Their Solution Using Symmetries. Cambridge University Press, Cambridge. [ Links ]
12. Hill J.M. (1992). Differential Equations and Group Methods for Scientists and Engineers. CRC Press, Boca Raton. [ Links ]
13. Ibragimov N.H. (ed.) (1994). CRC Handbook of Lie Group Analysis of Differential Equations, Vol. I: Symmetries, Exact Solutions and Conservation Laws. CRC Press, Boca Raton. [ Links ]
14. Ibragimov N.H. (ed.) (1995). CRC Handbook of Lie Group Analysis of Differential Equations, Vol. II: Applications in Engineering and Physical Sciences. CRC Press, Boca Raton. [ Links ]
15. Ibragimov N.H. (1999). Elementary Lie Group Analysis and Ordinary Differential Equations. Wiley, New York. [ Links ]
16. Hydon P.E. (2000). Symmetry Methods for Differential Equations: A Beginner's Guide. Cambridge University Press, Cambridge. [ Links ]
17. Noether E. (1918). Invariante Variationsprobleme. Kgl. Ges. Wiss. Nach. Math-phys. Kl 2, 235–269. [ Links ]
18. Leach P.G.L. and Naicker V. (2003). Symmetry, singularity and integrability: the final question? Trans. Roy. Soc. S. Afr. 58, 1–10. [ Links ]
19. Abraham-Shrauner B., Govinder K.S. and Leach P.G.L. (1995). Integration of second-order equations not possessing point symmetries. Phys. Lett. A 203, 169–174. [ Links ]
20. Nucci M.C. (1996). The complete Kepler group can be derived by Lie group analysis. J. Math. Phys. 37, 1772–1775. [ Links ]
21. Nucci M.C. and Leach P.G.L. (2001). The harmony in the Kepler and related problems. J. Math. Phys. 42, 746–764. [ Links ]
22. Nucci M.C. (1990). Interactive REDUCE programs for calculating classical, non-classical and Lie-Bäcklund symmetries of differential equations. Department of Mathematics, Georgia Institute of Technology, Atlanta. [ Links ]
23. Nucci M.C. (1996). Interactive REDUCE programs for calculating Lie point, non-classical, Lie-Bäcklund, and approximate symmetries of differential equations: manual and floppy disk. In CRC Handbook of Lie Group Analysis of Differential Equations, Vol. 3: New Trends in Theoretical Development and Computational Methods, ed. N.H. Ibragimov, pp. 415–481. CRC Press, Boca Raton. [ Links ]
24. Head A.K. (1993). LIE, a PC program for Lie analysis of differential equations. Comp. Phys. Commun. 77, 241–248. [ Links ]
25. Sherring J., Head A.K. and Prince G.E. (1997). Dimsym and LIE: symmetry determining packages. Math. Comp. Model. 25, 153–164. [ Links ]
26. Hereman W. (1994). Review of symbolic software for the computation of Lie symmetries of differential equations. Euromath. Bull. 2, 45–79. [ Links ]
27. Hereman W. (1996). CRC Handbook of Lie Group Analysis of Differential Equations. Vol. 3: New Trends. CRC Press, Boca Raton. [ Links ]
28. Nucci M.C. and Leach P.G.L. (2000). The determination of nonlocal symmetries by the method of reduction of order. J. Math. Anal. Appl. 251, 871–884. [ Links ]
29. Nucci M.C. and Leach P.G.L. (2002). Jacobi's last multiplier and the complete symmetry group of the Euler-Poinsot system. J. Nonlin. Math. Phys. 9, suppl. 2, 110–121. [ Links ]
30. Torrisi V. and Nucci M.C. (2001). Application of Lie group analysis to a mathematical model which describes HIV transmission. In The Geometrical Study of Differential Equations, eds J.A. Leslie and T.P. Hobart, pp. 11–20. American Mathematical Society, Providence . [ Links ]
31. Nucci M.C. (2003). Lorenz integrable system moves á la Poinsot. J. Math. Phys. 44, 4107–4118. [ Links ]
32. Marcelli M. and Nucci M.C. (2003). Lie point symmetries and first integrals: the Kowalevski top. J. Math. Phys. 44, 2111–2132. [ Links ]
33. González-Gascón F. and Gonzólez Lóápez A. (1983). Symmetries of differential equations. IV. J. Math. Phys. 24, 2006–2021. [ Links ]
34. Mahomed F.M. and Leach P.G.L. (1985). The linear symmetries of a nonlinear differential equation. Quæstiones Mathematicæ 8, 241–274. [ Links ]
35. Lemmer R.L. and Leach P.G.L. (1993). The Painlevé test, hidden symmetries and the equation . J. Phys. A: Math. Gen. 26, 5017–5024. [ Links ]
36. Kowalevski S. (1880). Sur le problème de la rotation d'un corps solide autour d'un point fixé. Acta Math. 12, 177–232. [ Links ]
37. Painlevé P. (1882). Sur les équations différentielles du second ordre et d'ordre supérieur dont l'intégrale générale est uniforme. Acta Math. 25, 1–85. [ Links ]
38. Gambier B. (1889). Sur les équations différentielles du second ordre et premier degré dont l'intégrale générale est a ses points critiques fixés. Acta Math. 33, 1–55. [ Links ]
39. Garnier R. (1912). Sur les équations différentielles du troisième ordre dont l'intégrale générale est uniforme et sur une classe d'équations nouvelles d'ordre supérieur dont l'intégrale générale a ses points critiques fixs. Ann. Sci. École Norm. Sup. XXIX, 1–126. [ Links ]
40. Chazy J. (1911). Sur les équations différentielles du troisième ordre et d'ordre supérieur dont l'intégrale générale a ses points critiques fixès. Acta Math. 34, 317–385. [ Links ]
41. Conte R. (ed.) (1999). The Painlevè Property: One Century Later. Springer-Verlag, New York. [ Links ]
42. Tabor M. (1989. Chaos and Integrability in Nonlinear Dynamics. John Wiley & Sons, New York. [ Links ]
43. Ramani A., Grammaticos B. and Bountis T. (1989). The Painlevé property and singularity analysis of integrable and nonintegrable systems. Phys. Rep. 180, 159–245. [ Links ]
44. Leach P.G.L., Cotsakis S. and Flessas G.P. (2001). Symmetry, singularity and integrability in complex dynamical systems: I The reduction problem. J. Nonlin. Math. Phys. 7, 445–479. [ Links ]
45. Miritzis J., Leach P.G.L. and Cotsakis S. (2000). Symmetry, singularities and integrability in complex dynamics IV: Painlevé integrability of isotropic cosmologies. Grav. Cosmol. 6, 282–290. [ Links ]
46. Ince E.L. (1927). Ordinary Differential Equations. Longmans, Green & Co., London. [ Links ]
47. Ablowitz M., Ramani A. and Segur H. (1978). Nonlinear evolution equations and ordinary differential equations of Painlevé type. Lett. Nuovo Cimento 23, 333–338. [ Links ]
48. Ablowitz M., Ramani A. and Segur H. (1980). A connection between nonlinear evolution equations and ordinary differential equations of P-type. I. J. Math. Phys. 21, 715–721. [ Links ]
49. Ablowitz M., Ramani A. and Segur H. (1980). A connection between nonlinear evolution equations and ordinary differential equations of P-type. II. J. Math. Phys. 21, 1006–1015. [ Links ]
50. Hua D.D., Cairó L., Feix M.R., Govinder K.S. and Leach P.G.L. (1996). Connection between the existence of first integrals and the Painlevé Property in Lotka-Volterra and Quadratic Systems. Proc. Roy. Soc. Lond. 452, 859–880. [ Links ]
51. Contopoulos G., Grammaticos B. and Ramani A. (1994). The mixmaster universe model revisited. J. Phys. A: Math. Gen. 27, 5357–5361. [ Links ]
52. Andriopoulos K. and Leach P.G.L. (2008). The Mixmaster Universe: the final reckoning? J. Phys. A: Math. Theor. 41, 155201, doi: 10.1088/1751-8113/41/ 15/155202. [ Links ]
53. Feix M.R., Géronimi C., Cairó L., Leach P.G.L., Lemmer R.L. and Bouquet S.E. (1997). On the singularity analysis of ordinary differential equations invariant under time translation and rescaling. J. Phys. A: Math. Gen. 30, 7437–7461. [ Links ]
54. Andriopoulos K. and Leach P.G.L. (2006). An interpretation of the presence of both positive and negative nongeneric resonances in the singularity analysis. Phys. Lett. A 359, 199–203. [ Links ]
55. Kermack W.O. and McHendrick A.G. (1927). A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. Lond. 115, 700–721. [ Links ]
56. Géronimi C., Feix M.R. and Leach P.G.L. (2001). Exponential nonlocal symmetries and nonnormal reduction of order. J. Phys. A: Math. Gen. 34, 10109–10117. [ Links ]
57. Leach P.G.L. and Govinder K.S. (1999). On the uniqueness of the Schwarzian and linearisation by nonlocal contact transformation. J. Math. Anal. Appl. 235, 84–107. [ Links ]
58. Abraham-Shrauner B. and Guo A. (1993). Hidden and nonlocal symmetries of nonlinear differential equations. In Modern Group Analysis: Advanced Analytical and Computational Methods in Mathematical Physics, eds N.H. Ibragimov, M. Torrisi and A. Valenti, pp. 1–5. Kluwer, Dordrecht. [ Links ]
59. Abraham-Shrauner B. and Leach P.G.L. (1993). Hidden symmetries of nonlinear ordinary differential equations. In Exploiting Symmetry in Applied and Numerical Analysis, eds E. Allgower, K. George and R. Miranda, pp. 1–10. American Mathematical Society, Providence. [ Links ]
60. Brauer F. (2002). Basic ideas of mathematical epidemiology. In Mathematical Approaches for Emerging and Reemerging Infectious Diseases, eds C. Castillo-Chavez, S. Blower, P. van den Driessche, D. Kirschner and A.A. Yakubu, pp. 31– 65. Springer-Verlag, New York. [ Links ]
61. Anderson R.M. (1988). The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS. J. Acquir. Immune Defic. Syndr. 1, 240–255. [ Links ]
62. Centers for Disease Control (1985). Update: acquired immunodeficiency syndrome in the San Francisco Cohort Study 1978–1985. Morb. Mortal. Wkly. Rep. 34, 573–575. [ Links ]
63. Jaffe H.W., Darrow W.W., Echenberg D.F., O'Malley P.M., Getchell J.P., Kalyanaraman V.S., Byers R.H., Drennan D.P., Braff E.H., Curran J.W. and Francis D.P. (1985). The acquired immunodeficiency syndrome in a cohort of homosexual men: a six-year follow-up study. Ann. Intern. Med. 103, 210–214. [ Links ]
64. Winkelstein W. Jr, Samuel M., Padian N.S., Wiley J.A., Lang W., Anderson R.E. and Levy J.A. (1987). The San Francisco Main's World Study: III. Reduction in human immunodeficiency virus transmission among homosexual/bisexual men, 1982–86. Am. J. Public Health 77, 685–689. [ Links ]
65. Géronimi C., Feix M.R. and Leach P.G.L. (2005). Properties of autonomous equations of the third and fourth order invariant under homogeneity symmetries in both dependent and independent variables. Prob. Nonlin. Anal. Engin. Syst. 11, 26–34. [ Links ]
66. Song B., Castillo-Chavez C. and Aparicio J.P. (2002). Tuberculosis models with fast and slow dynamics: the role of close and casual contacts. Math. Biosci. 180, 187–205. [ Links ]
67. Murphy G.M. (1960). Ordinary Differential Equations and their Solutions. Van Nostrand, Princeton. [ Links ]
68. Song B., Castillo-Chavez C. and Aparicio J.P. (2002). Global dynamics of tuberculosis models with density dependent demography. In Mathematical Approaches for Emerging and Reemerging Infectious Diseases: Models, Methods and Theory, eds C. Castillo-Chavez, S. Blower, P. van den Driessche, D. Kirschner and A.A. Yakubu, pp. 275–294. Springer-Verlag, New York. [ Links ]
69. Leach P.G.L. and Nucci M.C. (2004). An integrable S-I-S model. J. Math. Anal. Appl. 290, 506–518. [ Links ]
Received 7 March 2006. Accepted 14 October 2008.
* Author for correspondence E-mail: leachp@ukzn.ac.za
a Permanent address: School of Mathematical Sciences, University of KwaZulu-Natal, Private Bag X54001, Durban 4000, South Africa














