Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.105 n.3-4 Pretoria Mar./Apr. 2009
RESEARCH ARTICLES
Modelling of W UMa-type variable stars
P.L. Skelton*; D.P. Smits
Department of Mathematical Sciences, P.O. Box 392, UNISA 0003, South Africa
ABSTRACT
W Ursae Majoris (W UMa)-type variable stars are over-contact eclipsing binary stars. To understand how these systems form and evolve requires observations spanning many years, followed by detailed models of as many of them as possible. The All Sky Automated Survey (ASAS) has an extensive database of these stars. Using the ASAS V band photometric data, models of W UMa-type stars are being created to determine the parameters of these stars. This paper discusses the classification of eclipsing binary stars, the methods used to model them as well as the results of the modelling of ASAS 120036–3915.6, an over-contact eclipsing binary star that appears to be changing its period.
Key words: binaries: eclipsing, binaries: close, stars: individual, ASAS120036–3915.6
Introduction
Most of the stars in the sky are binary or multiple star systems. In only a small percentage of binary systems are the two stars far enough apart to be able to resolve the individual stars. The binary nature of close systems can be inferred from the periodic Doppler shifts seen in the spectral lines of the stars as they orbit their common centre of mass, or, if the orbital plane is inclined at an angle to the observer so that one star passes in front of the other, by variations in the observed brightness of the stars. These stellar systems are referred to as eclipsing binaries. The vast majority of eclipsing binaries have been found by searching for stars whose brightness varies periodically.
From Newton's Law of Universal Gravitation it can be shown that the square of the period P of a binary system is proportional to the sum of the masses m1 and m2 of the stars, i.e. P2 ∝ (m1 + m2). Measuring the period is relatively straightforward, and hence binary stars provide a convenient method of determining stellar masses. Because the mass of a star is the main characteristic that determines its properties, including how it changes with time, binary stars have contributed much to our understanding of stellar evolution. However, the origin, structure and evolution of close interacting binaries still hold many mysteries.1–5 Close binaries could evolve through angular momentum losses due to mass-loss in magnetised winds,6–10 or via thermal relaxation oscillations due to mass exchange between components,11–14 or a combination of both. It could be that during the course of their evolution, interacting binaries become semi-detached (see 'Binary star systems' for descriptions of the different types of systems). More observational data are needed to establish whether either one of the above mechanisms controls the evolution of close binaries, or whether some other as yet unidentified process is driving changes in the systems.
The period of an eclipsing binary changes with time due either to a redistribution of the matter between the stars, or when angular momentum is lost or gained by the system.15 For conservative mass exchange, the period decreases if mass is transferred from the more massive to the less massive star, and increases if the opposite occurs. By tidal dissipation orbital angular momentum may be transferred to or drawn from the spin motion of a star causing the period to either increase or decrease until a spin equilibrium is reached in which the tidal torque vanishes. A magnetised stellar wind can reduce the angular momentum of the system by magnetic braking, reducing the period. Period changes observed in binary systems do not have to be intrinsic phenomena. Light time effects (propagation delays) are produced when a binary system has another component that is in orbit about the common centre of mass of this system. Luminosity changes on parts of a binaries' photosphere can also lead to shifts in the time of minimum or maximum which would then appear as a period change.
Clearly, analysing systems undergoing period changes will help us to gain a better understanding of the important physical processes occurring in close binary systems. The All Sky Automated Survey16,17 (ASAS) is a project that has discovered thousands of variable stars since 1996, and continues to monitor them on a regular basis. Pilecki et al.18 searched the ASAS data for eclipsing binaries with observed high period change rates. From a sample of 1 711 systems that fulfilled all their criteria of data quality, they present 31 interacting binaries whose periods either increased (10) or decreased (21) in a five-year interval of observations.
In this article we report on another candidate, ASAS 120036– 3915.6, that appears to be changing its period. Methods used to classify eclipsing binary systems are discussed under 'Binary star systems', followed by a description of W UMa-type stars. Details of the ASAS project are presented under 'The All Sky Automated Survey', followed by the methods used to model W UMa-type stars from the dataset, together with results of modelling ASAS 120036–3915.6.
Binary star systems
Initially eclipsing binary star systems were classified according to their light curves.19 Three standard types were identified that are designated EA, EB and EW after their protostars Algol, β Lyrae and W Ursae Majoris (W UMa), respectively. Representative light curves for EA, EB and EW systems are shown in Fig. 1. The light curves of EA systems show a significant difference in the depths of their two minima. There are obvious start and end times for the eclipses, and outside the eclipses the light variations (magnitude changes) are almost negligible because the stars are well separated and do not interact significantly. Observationally it has been found that the orbital period for these stars is greater than one day. EB light curves display primary and secondary minima that have noticeably different depths and the light curve shows continuous variation outside of the eclipses. The orbital period is in general greater than one day. In EW systems the stars are very close so there is a continuous variation outside of the eclipses. Because of this the stars will experience gravitational distortion and heating effects. The difference between the primary and secondary minima is no more than 0.1 to 0.2 magnitudes because the stars are either of similar temperature or they have a common envelope. The difference between maximum and minimum is typically of the order of 0.75 magnitudes.

From classical mechanics it is well known that two gravitationally-bound masses m1 and m2 rotate about their common centre-of-mass C at velocities v1 and v2. In terms of the mass ratio q = m2/m1 with m2 < m1, it is straightforward to show that

If the orbital plane is tilted by an angle i with respect to the plane of the sky, the maximum velocity measured will be vmax = v sin i, where v is the velocity.
A convenient way of describing and classifying binary star systems is in terms of the Roche model. Consider a system of two point masses m1 and m2 with m1 > m2 in circular orbit about their common centre-of-mass. Choose a reference frame with its origin at m1 that is co-rotating with the system at an angular velocity ω. Let m2 be at the point (a, 0, 0), with the z-axis perpendicular to the orbital plane, as illustrated in Fig. 2.
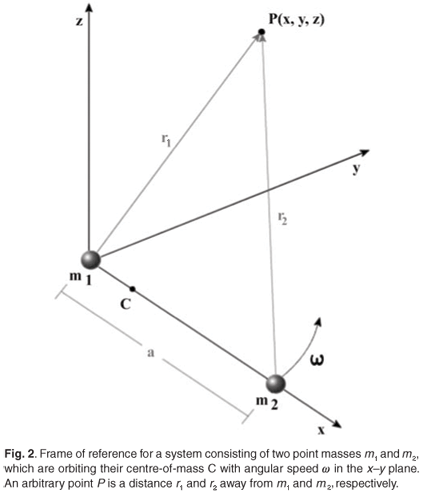
The gravitational potential Φ experienced by a third body with infinitesimal mass at any point P(x, y, z) will be the sum of the potential of the two point masses and the centrifugal potential due to the rotation of the system. That is

with
 and
and  ,
,
where G is the gravitational constant. The shape of the potential in 3D space is defined by the separation between the two stars, a, and the mass ratio q = m2/m1. For a binary system with a mass ratio q = 0.3 the equipotential surfaces in the rotating frame of reference are shown in Fig. 3. The equipotential surfaces of the two masses meet at several points. The inner Lagrangian point L1 is the point between the two masses where the potential of the masses exactly cancel, forming a figure-of-eight shape in Fig. 3. The 3D lobes that form this equipotential are called Roche lobes.

The application of this model to binary stars is apparent when it is recognised that the surface of a star forms an equipotential surface. The normal of an equipotential surface gives the direction of the local effective gravity. For a single non-rotating star the equipotential surfaces are spherically symmetrically centred on the centre of mass. The shape of each star in a binary system with a circular orbit is defined by an equipotential surface as given by the Roche model. The Roche lobes define the upper limit for the volume of each star for which all its matter is under its own gravitational control. Because the gravitational and centrifugal influence of both stars cancel each other at L1, matter can flow from one star to the other through this point. If matter lies between the Roche lobes and the surface that goes through L2, this material forms a common envelope around the stars. At L2 matter can escape from the system.
Using the idea of Roche lobes and the critical surfaces, eclipsing binaries can be separated into morphological classes. If the stars are far apart, the mass of each star is contained within equipotential surfaces that are essentially spheres around the centre of each star. As the ratio of their separation to their radii decreases, the shape of the star becomes distorted by the gravitational influence of its neighbour. Provided the photospheres of both stars lie within their Roche lobes, the binary is referred to as a detached system. EA light curves are typical for detached systems although the prototype of the class, Algol, is a semi-detached system. In a semi-detached system, one component's photosphere lies within its Roche lobe while the other star's photosphere coincides with its Roche lobe. In these systems, mass transfer takes place between the two components through L1. The shape of the Roche lobe-filling star in semi-detached systems is non-spherical; therefore the surface area seen by an observer changes throughout the orbital cycle. The observed flux is proportional to the surface area, and hence the light curve varies continuously between eclipses, producing EB light curves. EB light curves can also be produced by detached, semi-detached and, in some cases, marginally over-contact systems. In contact binaries, the photospheres of both stars equal their Roche lobes, while in over-contact binaries the photospheres of both stars exceed their Roche lobes. Often these stars are referred to as common envelope binaries because they effectively share a common stellar atmosphere. This common envelope will tend to equalise the surface temperatures of the stars.
EW stars
EW stars, or W UMa-type variable stars, are over-contact eclipsing binary systems that have orbital periods between 0.2 day and 1 day. Each component is a main sequence star (i.e. it burns hydrogen in its core) with spectral type ranging from A to K. Both the spectral type and the colour of an EW star do not change during the orbital cycle. This implies that the common envelope is optically thick and has a nearly uniform temperature. Temperature differences of only a few hundred Kelvin are found between the two components. The mass ratio q lies between 0.08 and 0.8. Spectral features for these stars include rotationally broadened and blended absorption lines.15 There are also emission lines in the ultraviolet spectrum which is an indication that these stars are chromospherically active.
Circular orbit binaries, such as EW stars, exhibit synchronous rotation which means that the spin period of each component equals the orbital period. Compared to the sun, which has a spin period of ~29 days, EW systems with periods of less than a day are very fast rotators. Magnetic fields in stars are believed to be produced by differential rotation of the photosphere and hence the faster a star rotates, the stronger the field it can generate. Because EW stars are rotating rapidly, they could be expected to be more magnetically active than stars with longer rotational periods. Some EW stars are suspected of being magnetically active because the primary and secondary maxima in the light curves have different magnitudes. Known as the O'Connell effect,15 this phenomenon is generally attributed to the presence of spots on the surfaces of the stars which is an indicator of strong magnetic fields. From observations made in the X-ray, visual, ultraviolet and radio regimes,20 over-contact binary stars were found to have magnetic activity levels lower than those measured for single, rapidly-rotating stars. This suggests that the common envelope suppresses dynamo action to some extent.
EW stars are also known to exhibit complex period patterns where intervals of constant period are interrupted with intervals where the period increases and/or decreases. A statistical study by van't Veer21 found that positive and negative period jumps are randomly distributed. In some cases, the period of the stars can be found to be only increasing or decreasing and showing no intervals where the period is constant.
Binnendijk22 divided EW stars into two subclasses which he called A-type and W-type. The classification depends on whether the larger or smaller component has the higher temperature. In the A-type systems the larger component has the higher temperature whereas in the W-type systems the smaller component has the higher temperature. Observationally it has been found23 that the A-type systems tend to have low mass ratios (q < 0.3) and spectral type from A to F. W-type systems usually have mass ratios q > 0.3 and spectral types of G or K. In most cases, the orbital periods of W-type systems are smaller than those of the A-types.24 The O'Connell effect is noted more in the light curves of the W-type systems, suggesting that they are more magnetically active than the A-type systems. Currently, there is no clear indication whether there is an evolutionary link between the two subclasses, or whether they form and evolve along separate paths.
The All Sky Automated Survey
The All Sky Automated Survey16 (ASAS) is a project that was set up in 1996 to detect and monitor the variability of stars between 8th and 12th magnitude in the V and I bands south of declination +28°. Observations are carried out at the Las Campanas Observatory in Chile using telescopes with an aperture of 7 cm and a focal length of 20 cm; one telescope is equipped with a standard V-band (5 500 Å) filter and the other with an I-band (9 000 Å) filter. Images of an 8° × 8° field of view are captured on 2K × 2K CCD cameras. About 60% of the sky is visible from the observatory. All stars are observed once per one to three nights, weather permitting. When observations are performed, several flat-field and dark exposures are taken followed by more than a hundred three-minute exposures. This creates a raw data stream of 1.5–2 GB per instrument per night.
Simultaneous photometry is performed through different apertures ranging from 2–6 pixels in diameter. All the data are processed separately so that for faint objects the data from the smallest aperture are used and for bright objects data from the largest aperture are used. Each measurement is then graded according to the quality of the data. Every star observed is given an ASAS identification that is coded from the star's right ascension and declination (coordinates) e.g. ASAS 120036–3915.6 has a right ascension of 12h00m36s and a declination of –39°15'36" (the minus sign indicates that the star lies in the southern celestial hemisphere). Cross references have been made to stars listed in other catalogues. The project has already discovered over 50 000 variable stars. Of these, more than 5 000 have been classified as eclipsing contact binaries. Many of these stars have not been classified previously as variable stars.
The ASAS data are publicly available via the internet. The data for each star have been flux-calibrated into standard Johnson V band magnitudes, as well as being separated into different categories of variable stars. The eclipsing binaries are subdivided using a Fourier analysis method developed by Rucinski.25 Expressing the time-dependent V magnitudes V(t) as a Fourier series

it has been found that plotting the amplitude of the fourth harmonic, a4, against the amplitude of the second harmonic, a2, for each star, the eclipsing systems divide into three regions. As can be seen in Fig. 4, eclipsing contact (EC) (which includes contact and over-contact systems), eclipsing semi-detached (ESD) and eclipsing detached (ED) systems can be distinguished from their position in the a2–a4 plane except for small regions of overlap where there is uncertainty. Stars falling in areas of overlap between the groups will need follow-up observations and/or further data analysis to decide their classifications. ASAS also provides the orbital period P of the binary, the epoch of minimum brightness T0, the maximum magnitude Vmax, and the change in V band magnitude ΔV.

Modelling of eclipsing binaries
ASAS data
To obtain a unique model of a W UMa system requires both photometric and spectroscopic data. The period of the system can be determined from timing of the minima in the light curve and many of the system parameters can be determined from the shape of the folded light curve (phase-magnitude plot), but unless the mass ratio q is known, a unique solution cannot be obtained. In choosing systems from the ASAS database for further studies, we concentrated on systems with periods P ~ 0.3 d so that a complete cycle could be observed during a single night of observing. Both photometric and spectroscopic data can then be obtained. Radial velocity amplitudes for EW stars are in the range of 100–300 km s–1. Radial velocities with accuracies typically better than 10 km s–1 are needed to measure v sin i for at least one of the components to constrain the range of allowable solutions for a system. One instrument that is capable of measuring radial velocities of W UMa stars is the South African Astronomical Observatory's Grating High Resolution Echelle Spectrograph known as GIRAFFE, which can be attached to the 1.9-m telescope at Sutherland. The sensitivity of this instrument limits one to stars brighter than 10th magnitude, so this was one constraint that was imposed in choosing suitable candidates from the sample.
Because ASAS makes only one measurement on each star about every three days, a complete light curve (plot of magnitude versus time) over a full phase is not seen. However, because the variations from one cycle to the next are very small, by running the data through a period analysis routine, the fundamental period P of the system can be determined. By folding all the measurements on this period, a phase-magnitude plot can be made which can be used to model the systems. Phase values ø are fractional values of the period with values between 0 and 1 calculated from

where HJD is the Heliocentric Julian date of the observation, T0 is an epoch of primary minimum and P is the orbital period of the binary system. The Julian date is defined to be the number of days that have elapsed since mean noon at Greenwich on 1 January 4713 BC. When measuring the period of variable stars to an accuracy of a second or less, it is important to remove any light propagation delay effects that might arise from the position of the Earth in its orbit about the Sun. Heliocentric Julian date is the Julian date time system with its frame of reference centred on the Sun.
The light curve data (HJD versus magnitude) provided by ASAS were converted into a phase-magnitude diagram by folding the data from the appropriate aperture in a spreadsheet on the period P as given in the ASAS database, using their epoch T0 for zero phase. Interesting features to look for in the folded data are flat-bottomed minima indicating a totally eclipsing system, where one star is completely covered by the other, and magnitude differences between the maxima (the O'Connell effect) suggesting the presence of spots and hence enhanced magnetic activity.
Light curve modelling
The light curve synthesis programme we are using to model binary star systems is a commercial package known as Binary Maker 3.0. The programme calculates light and radial velocity curves using system parameters that the user inputs. By computing the residual R formed from the sum of the differences between the observed (O) and calculated (C) light curves, (R = Σi (Oi–Ci)2), parameters can be adjusted to give a 'best fit' to the data by minimising the residuals. Binary Maker 3.0 also creates a rendering of the system. The starting point to the modelling is the phase-magnitude data.
A parameter that plays a vital role in modelling binary stars is the mass ratio q. When radial velocity measurements are available the mass ratio for the system is simply the inverse of the measured peak radial velocity ratio of the two components (see Eq. 1). If only photometric data are available, the mass ratio of the system is not known, and a unique solution cannot be determined. The reason for this non-uniqueness is that similar values of a minimum residual can be obtained for a range of different parameters which include q. It is possible to restrict the range of values for the mass ratio by using an iterative procedure in which certain parameters are adjusted for each given value of q.26 By plotting the residual values against the mass ratio values it is easy to identify which mass ratios give the lowest residual values. For systems with a total eclipse, additional constraints are placed on the geometry of the system which restricts the range of possible values for q significantly.
Another important parameter to consider is the fillout factor for the system. For an over-contact system, the fillout parameter f is defined as

where Ωinner is the value of the inner critical Roche equipotential and Ωouter is the value of the outer critical Roche equipotential. If the surface potential is in contact with the inner critical surface then f = 0, whereas if the surface potential is in contact with the outer critical surface then f = 1. The value of the fillout parameter for the system is a measure of how much of the volume between the inner critical surface and the outer critical surface is filled by the binary's photosphere. For an over-contact system the value for f lies between 0 and 1. As a starting value for the fillout parameter, we used the average value f = 0.15 for over-contact systems.
The temperature parameters required by Binary Maker 3.0 refer to the mean effective temperature Teff of the stars. One method of estimating the temperature of a star is to measure the difference in magnitude of its luminosity through two different filters and then look up tabulated values of temperature versus colour index27 (such as B – V or V – I). ASAS only provide V magnitudes at this stage, so values for B were obtained from the SIMBAD database.28 Unfortunately, the values listed were not obtained at a specific phase and hence could contain errors of a few tenths of a magnitude with respect to the V value. If Teff > 7 200 K energy from the core is transported outwards predominantly by radiation and the stars are called radiative; if Teff < 7 200 K the dominant energy transport mechanism is convection and the stars are called convective.
The next parameters that are entered are the gravity darkening, limb darkening and reflection coefficients. Gravity darkening is caused by the fact that the local surface gravity on a non-spherical star varies across the surface of the star. The flux that emerges from the star is proportional to the local gravity and hence there is a pole-to-equator variation in the brightness of the star. For convective stars the gravity brightening coefficient is29 α = 0.32 while for radiative stars α = 1 is used. A star's surface brightness also decreases as one looks from the centre of the star to the limb of the star. When looking at the centre of a star, an observer's line of sight passes through the deeper, hotter layers of the star. At the limb, the line of sight passes through the upper, cooler layers of the star. This results in the surface brightness decreasing from the centre to the limb of the disk. The limb darkening law used by Binary Maker 3.0 is

where I(0) is the intensity at the centre of the disc, x is the limb-darkening coefficient and θ has a value between 0° and 90° where θ = 0° corresponds to the centre of the disc and θ = 90° corresponds to the limb of the disc. These values are wavelength and temperature dependent. We used the tabulated values of van Hamme.30 The reflection coefficient is a measure of how much incident radiation from one star is re-radiated by its companion. For radiative stars a reflection coefficient of 1.00 was used, while for convective stars a value of 0.50 was applied.31
The inclination angle i is a measure of the angle between the orbital plane of the binary and the observer's line-of-sight. An inclination of 0° means that the system is viewed looking down on the poles of the stars and i = 90° means it is viewed edge-on. If the light curve exhibits a minimum with a flat bottom then one component is being totally eclipsed by the other. If the two components are of roughly the same size, the inclination angle must be close to 90° for a total eclipse to occur. If one star is much larger than its companion, total eclipses can occur for inclination angles up to about 75°.
Once all the parameters are entered into the system, a calculated light curve can be rendered. Parameters can then be adjusted until the lowest value for the residuals is obtained.
ASAS 120036–3915.6
Model using full dataset
The eclipsing contact system catalogued as 120036–3915.6 in the ASAS database is listed as having Vmax = 10.45 and a period P = 0.292670 d. Folding the data on this period resulted in a smeared-out curve. Experimenting with different periods, it was found that using P = 0.292672 d produced a plot with the least scatter. The phase-magnitude diagram is shown in Fig. 5. This period was adopted for further analysis and produced a phase-magnitude curve with a flat bottomed secondary eclipse. Because the primary minimum occurs when the hotter, larger star is eclipsed, this indicates an A-type system which is expected to have q < 0.3. Values of B and V obtained from SIMBAD give B – V = 0.8 which corresponds to a surface temperature Teff = 5 200 K, indicating a late G-, early K-type star which is a later spectral type than is expected for an A-type system. The orbital period of P ~ 0.3 d is more typical of W-type systems than A-type systems.
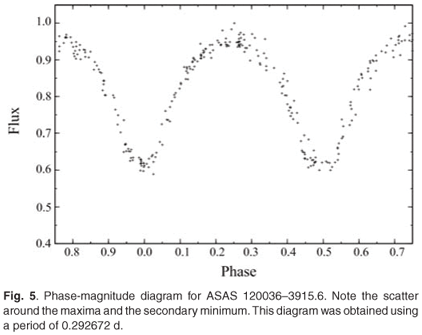
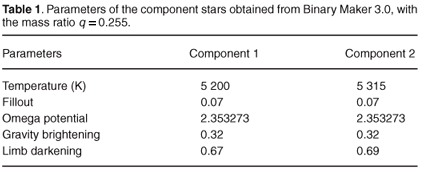
To determine a mass ratio for the system, an iterative procedure was employed. The temperature of the primary component was set to 5 200 K while the inclination angle, the fillout and temperature of the secondary component were varied until the residual was minimised. The process was repeated with a range of mass ratios until the lowest residual was obtained. This occurred for q = 0.255 which was adopted as the mass ratio of the system. The final model for the system has T1 = 5 200 K, T2 = 5 315 K, f1 = f2 = 0.07 and i = 81.2°. Parameters of the component stars are listed in Table 1. The calculated light curve and the residuals for the system are shown in Fig. 6 along with a rendering of the system. From the residuals it is clear that the calculated curve is not an ideal fit to the data. This is probably due to smearing of the data due to a change in the period of the system.

A surprising result of the model is that T2 > T1 which indicates a W-type rather than A-type system. The reason that the secondary minimum occurs when the hotter star is eclipsed could be due to the effects of limb darkening and gravity darkening reducing the flux from the smaller star. Spectroscopic data have been obtained for this star (from GIRAFFE) and are currently being analysed.
Model with period change
The orbital periods determined by ASAS are an average over the whole dataset. Systems whose periods are changing with time cannot be distinguished in their processing procedure, but the folded data will produce phase-magnitude plots with scatter. 120036–3915.6 was not identified by Pilecki et al.18 as having a variable period, but with only 278 A or B quality data points, it would have been eliminated from their sample at an early stage of their investigation (they required at least 300 acceptable quality data points).
To investigate if 120036–3915.6 has undergone a period change, the data were split into two intervals. Using the ASAS period of 0.292670 d to fold the data, phase-magnitude diagrams for both intervals were created. The curve for the first interval looked reasonable, whereas for the second interval the primary minimum was shifted away from phase 0 and the secondary minimum was smeared out. The period for the second interval was modified to 0.2926715 d which reduced the scatter in the data. This implies that the period of the system changed during the observing period. These phase-magnitude diagrams were imported into Binary Maker 3.0 and the model solution obtained using all the data was then applied to the separate diagrams. The calculated light curve and the plot of the residuals for the first and second interval are shown in Fig. 7a and Fig. 7b, respectively.

Conclusion
Using ASAS data for the eclipsing over-contact binary 120036–3915.6 we have modelled the light curve to determine the physical parameters of the system. It appears to be an A-type system with a mass ratio q = 0.255 although the spectral type, period and T2 > T1 suggest that the system is a W-type system. The mass ratio that we have determined can be verified by radial velocity measurements. The smeared out phase-magnitude plots created from a single period suggest that the orbital period is changing. Further observations are required to confirm if this is the case and, if so, it should continue to be monitored and modelled. If data of sufficient quality is obtained, it might be possible to establish from the models which parameters are changing, and hence what mechanism is operating to change the period. Data from the SuperWASP32 (Wide Angle Search for Planets) database have been obtained for ASAS 120036–3915.6 and are currently being used to refine the model obtained from the ASAS data. SuperWASP provides an effective temperature for the system obtained from the 2MASS33 (Two Micron All Sky Survey) project. The 2MASS temperature is 5 192 K which is close to the temperature obtained from SIMBAD suggesting that there is little interstellar reddening towards the star. Once the spectroscopic data have been analysed, the spectroscopic value for q might allow the model to be refined further.
We would like to thank A. Prozesky for Figs 2 and 3. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
1. Paczyński B. (1971). Evolutionary processes in close binary systems. Annu. Rev. Astron. Astrophys. 9, 183. [ Links ]
2. Robertson J.A. and Eggleton P.P. (1977). The evolution of W Ursae Majoris systems. Mon. Not. R. Astron. Soc. 179, 359–375. [ Links ]
3. Webbink R.F. (2003). Contact binaries in 3D stellar evolution. In Astronomical Society of the Pacific Conference Series 293, eds S. Turcotte, S.C. Keller and R.M Cavallo, p. 76. Astronomical Society of the Pacific, San Francisco. [ Links ]
4. Yakut K. and Eggleton P.P. (2005). Evolution of close binary systems. Astrophys. J. 629(2), 1055–1074. [ Links ]
5. Eker Z., Demircan O., Bilir S. and Karatas Y. (2006). Dynamical evolution of active detached binaries on the log Jo – log M diagram and contact binary formation. Mon. Not. R. Astron. Soc. 373(4), 1483–1494. [ Links ]
6. Vilhu O. (1982). Detached to contact scenario for the origin of W UMa stars. Astron. Astrophys. 109(1), 17–22. [ Links ]
7. van't Veer F. and Maceroni C. (1989). The angular momentum loss for late-type stars. Astron. Astrophys. 220(1), 128–134. [ Links ]
8. Stępień K. (1995). Loss of angular momentum of cool close binaries and formation of contact systems. Mon. Not. R. Astron. Soc. 274, 1019–1028. [ Links ]
9. Ibanoglu C., Soydugan F., Soydugan E. and Dervisoglu A. (2006). Angular momentum evolution of Algol binaries. Mon. Not. R. Astron. Soc. 373(1), 435–448. [ Links ]
10. Pribulla T. and Rucinski S.M. (2006). Contact binaries with additional components. I: The Extant Data. Astron. J. 131(6), 2986–3007. [ Links ]
11. Lucy L.B. (1976). W Ursae Majoris systems with marginal contact. Astrophys. J. 205, 208–216. [ Links ]
12. Flannery B.P. (1976). A cyclic thermal instability in contact binary stars. Astrophys. J. 205, 217–225. [ Links ]
13. Wang J.M. (1999). Contact discontinuities in models of contact binaries undergoing thermal relaxation oscillation. Astron. J. 118(4), 1845–1849. [ Links ]
14. Qian S. (2003). Are overcontact binaries undergoing thermal relaxation oscillation with variable angular momentum loss? Mon. Not. R. Astron. Soc. 342(4), 1260–1270. [ Links ]
15. Hilditch R.W. (2001). In An Introduction to Close Binary Stars. Cambridge University Press, Cambridge. [ Links ]
16. Paczyński B., Szczygieł D.M., Pilecki B. and Pojmański G. (2006). Eclipsing binaries in the All Sky Automated Survey catalogue. Mon. Not. R. Astron. Soc. 368(3), 1311–1318. [ Links ]
17. All Sky Automated Survey. Online at: http://archive.princeton.edu/~asas. [ Links ]
18. Pilecki B., Fabrycky D. and Poleski R. (2007). All-Sky Automated Survey eclipsing binaries with observed high period change rates. Mon. Not. R. Astron. Soc. 378, 757–767. [ Links ]
19. Kallrath J. and Milone E.F. (1999). In Eclipsing Binary Stars: Modelling and Analysis, chap. 1, pp. 1–21. Springer-Verlag, New York. [ Links ]
20. Rucinski S.M. and Seaquist E.R. (1988). VLA observations of the contact binary VW Cep. Astron. J. 95(6), 1837–1840. [ Links ]
21. van't Veer F. (1991). The period variation of W Ursae Majoris binaries and their relation to magnetic activity. Astron. Astrophys. 250(1), 84–88. [ Links ]
22. Binnendijk L. (1970). The orbital elements of W Ursae Majoris Systems. Vistas Astr. 12, 217–256. [ Links ]
23. Csizmadia S. and Klagyivik P. (2004). On the properties of contact binary stars. Astron. Astrophys. 426, 1001–1005. [ Links ]
24. Wadhwa S.S. (2005). Photometric analysis of southern contact binary stars, part 1: GZ Pup, AV Pup and II Aps. Astrophys. Space Sci. 300, 289–296. [ Links ]
25. Rucinski S.M. (1973). The W UMa-type systems as contact binaries. I: Two methods of geometrical elements determination. Degree of contact. Acta Astronom. 23(2), 79–120. [ Links ]
26. Wadhwa S.S. and Zealey W.J. (2004). UX Ret and CN Hyi: Hipparcos Photometry Analysis. Astrophys. Space Sci. 295, 463–472. [ Links ]
27. Cox A.N. (ed.) (2000). Allen's Astrophysical Quantities, 4th edn, p. 388. Springer-Verlag, Heidelberg. [ Links ]
28. SIMBAD. Astronomical Database. Online at: http://simbad.u-strasbg.fr/ simbad/ [ Links ]
29. Lucy L.B. (1967). Gravity-darkening for stars with convective envelopes. Z. Astrophys. 65, 89–92. [ Links ]
30. van Hamme W. (1993). New limb-darkening coefficients for modelling binary star light curves. Astron. J. 106, 2096–2117. [ Links ]
31. Ruckinski S.M. (1969). The photometric proximity effects in close binary systems. II: The bolometric reflection effect for stars having deep convective envelopes. Acta Astronom. 19, 245–255. [ Links ]
32. Wide Angle Search for Planets. Online from: http://www.superwasp.org/ [ Links ]
33. Two Micron All Sky Survey. Online from: http://www.ipac.caltech.edu/2mass/ [ Links ]
Received 29 February 2008. Accepted 14 April 2009.
* Author for correspondence E-mail: skeltpl@unisa.ac.za














