Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.11-12 Pretoria Nov./Dec. 2008
RESEARCH ARTICLES
Co-authorship networks in South African chemistry and mathematics
Ian N. DurbachI, *; Deevashan NaidooI; Johann MoutonII
IDepartment of Statistical Sciences, University of Cape Town, Private Bag, Rondebosch 7001, South Africa
IICentre for Research on Science and Technology, University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
ABSTRACT
Co-authorship networks are graphs in which the nodes of the graph represent authors and two authors are connected by an edge if they have written one or more papers together. When applied to the authorship of scholarly papers, analysing the structure of a co-authorship network can provide useful insights into the way in which research is carried out in a particular field. We examine two co-authorship networks in our article, constructed from papers written on the subjects of chemistry and mathematics during the period 1990 to 2005, in which at least one of the authors was South African. Local results are compared with other studies conducted in much larger discipline-wide networks. We find that many of the same patterns exist locally, with the main difference being a far more fragmented South African mathematics network. We discuss some tentative implications of these results.
Introduction to co-authorship networks
Collaboration between academic scientists, or any other researchers for that matter, is a complex mix of formal and informal processes, many of which are difficult to measure at all, let alone accurately. One mode of measurement that has proved useful has been to examine patterns of co-authorships between scientists working in a particular field. The co-authorship of a scholarly paper by two or more authors represents a tangible output of collaboration between these authors, and this form of analysis has become increasingly popular with increases in the scale of online bibliographies and reference databases. These co-authorships form a so-called 'co-authorship network' in which the nodes of the network represent authors, and an edge connects two authors if they have co-authored one or more papers. Analysis of the structure of these networks can provide useful insights about the nature of research and especially collaborative research in that discipline. Given the importance of scientific collaboration for increased productivity and shared expertise, insights into the nature of such collaboration are of considerable value.
The analysis of co-authorship patterns has its beginnings in information science and in bibliometrics1,2 in particular, South African examples of which can be found in several papers by Pouris.3,4 But these studies typically do not attempt to reconstruct entire co-authorship networks. Several authors have considered co-authorship networks over the past decade, constructed from enormous online databases aimed at capturing research in whole fields of enquiry. Newman5–8 studied co-authorship networks in several areas of scientific research in a series of papers: biomedicine, physics (including separate analyses of theoretical physics and high-energy physics, sub-fields of physics in which research is conducted in very different ways), mathematics, and computer science. Barabási et al.9 have also examined co-authorship networks in science, this time in mathematics and neuroscience, while in the social sciences, Moody10 has studied a co-authorship network constructed from entries in Sociological Abstracts over a period of 35 years. We conduct a smaller-scale study in our paper, examining co-authorship networks constructed from research involving South African scientists. We use two disciplines, chemistry and mathematics, commonly believed to support different ways of doing research—modes of research in chemistry being a mixture of experimental and theoretical work whereas those in mathematics are almost exclusively theoretical. Collaboration patterns in South African scientific research have previously been studied11 using bibliometric analyses of survey data, but to our knowledge, this is the first study to reconstruct entire co-authorship networks within disciplines, and perform analyses thereof.
Data and methods
The networks have been constructed from the South African Knowledgebase publication data maintained by the Centre for Research on Science and Technology (CREST) in Stellenbosch and covering the period 1990 to 2005. The data we used are from papers recorded in the ISI-citation indexes or articles in South African accredited journals, so that while not every published paper is documented, the networks can be seen as a reasonable reflection of high-quality research over the last 15 years (see the CREST website http://academic.sun.ac.za/crest/research/sakb.htm for further details on the database)ª. We use this database in particular because it is the most complete publications record available to us that includes regional affiliation. Each author and paper is uniquely identified, which affords the basis for the construction of the co-authorship networks. The database contains publication information on papers that include at least one author affiliated to a South African institution (hereafter referred to as 'South African') in the list of authors, so that the resulting co-authorship network contains both local and foreign—that is, affiliated to an institution outside South Africa—authors. The inclusion of foreign authors is essential, because they constitute a significant part of South African-related research—some 33% of all authors in the database are foreign—but this creates certain methodological problems. A specific instance arises from co-authorship between foreign authors that exclude a South African scientist; this is not captured in the database. The consequence is that the various statistics gathered (especially the numbers of papers published and numbers of co-authors) are likely to be under-represented for those foreign authors appearing in the database, as their publications are only partly included, and the networks may appear to be more fragmented than they would be if co-authorship between foreign scientists alone was also included. More correctly, links between two scientists should be interpreted as indicating co-authorship, conditional upon a South African being involved, rather than unconditional co-authorship. When either of the two scientists is South African, this requirement is naturally fulfilled. But note that this type of collaboration can also occur where neither of two parties is South African, but a third author to the paper is South African. The results gathered for foreign scientists therefore represent that part of their output that includes some South African involvement.
Preliminary authorship and co-authorship statistics
Table 1 provides a summary of the basic statistics in the two networks. In each of the networks there is a single paper co-authored by a large number of people (42 authors in chemistry, 43 in mathematics), the vast majority not co-authoring any further papers, i.e. that paper is their sole contribution. While large-scale collaborative research of this kind is an important feature of modern research, in relatively small networks such as those covered by this study it also has the potential to skew some of the network statistics, particularly the average number of co-authors. Table 1 therefore provides summary statistics with these two papers both included (full network) and excluded ('outlier' removed), although attention is focused on the statistics for the full network.
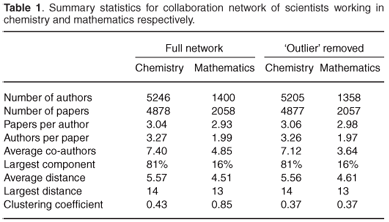
Chemistry is clearly the larger of the two networks, with 5246 authors and 4878 papers. In comparison, the mathematics network contains roughly a third of the authors and 40% of the papers. The number of papers written per author is very similar across the two subjects. Chemists authored on average 3.04 papers over the 15-year period, whereas mathematicians authored 2.93. Publication productivity for mathematicians is roughly consistent with that reported by Newman for the broader databases maintained by the Mathematical Reviews journal,8 reporting an average of 6.9 papers over a 60-year period (the figures are in rough agreement if one assumes an average research career of about 30 years). Moed12 reports in his analysis of the productivity of scientists in various disciplines an estimate of 2.5 papers per active scientist in chemistry and 1.4 papers per active scientist in mathematics in 1998. Moed's data are only based on papers recorded in the ISI Web of Science. His data imply that the overall productivity of South African scholars is good, and extremely competitive, when measured against world statistics.
While the number of papers per author is similar between subjects, the number of authors per paper differs considerably and is substantially larger in the chemistry network than in the mathematics network. Chemistry papers are co-authored by an average of 3.27 authors, while mathematics papers are co-authored by an average of 1.99 authors. Both these numbers are slightly lower but still in basic agreement with Glänzel's international analysis,13 which reports 3.7 and 2.5 authors per chemistry and mathematics paper, respectively. This pattern is also reflected in the larger number of co-authors that scientists in the chemistry network have in relation to their counterparts in the mathematics network. Over the 15-year period, those in the chemistry network published with an average of 7.4 scientists (author, with 6.4 other co-authors) while those in mathematics co-authored with only 4.9 (author, with 3.9 co-authors). The effect of the 'outlier' papers in inflating the average number of co-authors is evident, particularly in the smaller mathematics network. What is clear is that under either inclusion or exclusion of these outliers the extent of co-authorship is considerably greater in chemistry than in mathematics, presumably reflecting meaningful differences in the way research is carried out in the two subjects. These results are largely consistent with what has been reported in other studies.5,8,9
Measuring the connectivity of scientific communities
The remainder of Table 1 provides further network statistics that perhaps require some explanation for readers less familiar with network analysis. A component is a collection of nodes that are connected to each other by one or a series of edges, so that each node in the component can be reached from every other node in the component by travelling along a series of edges. The largest component is simply the component in the network that contains the largest number of nodes, that is, authors. For the chemistry network, the largest component covers some 81% of authors in the database. This figure is consistent with results obtained for similar mixed experimental-theoretical disciplines such as physics.8 The fact that a large proportion of authors can be linked to one another through a series of connections indicates a type of research community through which a shared research enterprise exists and can be traced through various inter-connected groups of authors. In contrast, the largest component in the mathematics network covers only 16% of authors in that database, which is considerably lower than the 82% reported for the Mathematical Reviews dataset8 and the 70% reported by Barabási.9 The reasons for this difference are not immediately clear. In part, they may be due to a combination of the large number of foreign authors (36% of all authors) and the small number of authors per paper (which make it more difficult for connections to form between foreign authors), but they also suggest a research landscape in which many relatively small pockets of researchers work separately in isolation from one another.
Another concept that has been popular in the analysis of network structure is network distance. The distance between any two nodes in a network is the number of edges that must be traversed in order to reach one node from the other, and is a measure of how closely linked those two nodes are. Authors that have co-authored a paper together have a distance of one; two authors who have not written a paper together but have each co-authored a paper with a common third party have a distance of two; and so on. The notion of distance is behind the famous Erdös number that gives anyone's proximity to this prolific mathematician.14 The average distance between pairs of authors in the chemistry network tends to be slightly higher than between author pairs in the mathematics network, which at first glance seems to run contrary to earlier results intimating a more collaborative environment in chemistry. However, these results are largely due to the smaller size of the mathematics network. Many of the author pairs in the mathematics network are not connected at all (as is shown by the relatively small size of the largest connected component), and distance measurements are only computable for those pairs of authors that can be connected via some path. Thus, the interpretation of average distance needs to account for this exclusion of author pairs that cannot be connected at all. The smaller average distance observed in the mathematics network is therefore consistent with the notion that research in mathematics tends to be carried out by smaller groups working in a relatively isolated environment.
Finally, one can also examine the degree of clustering in each of the networks, which measures the probability that two of a scientist's co-authors have themselves co-authored a paper together, in which case the three authors form a transitive triple. The clustering coefficient of the full mathematics network is considerably higher than that of the chemistry network, but this is clearly shown to be an artefact introduced by the large number of transitive triples contributed by the inclusion of a single paper with many co-authors. Both networks show similar degrees of clustering after removing this particular paper. This result is somewhat surprising, because one might expect the chemistry network, which has a far greater proportion of papers with three or more authors (that naturally introduce connected triples of authors), to exhibit a higher clustering coefficient than the mathematics network. However, the results are largely consistent with previous research,5 where similarly large clustering coefficients of between 0.3 and 0.5 were observed, except in a very highly collaborative high-energy physics network, where the degree of clustering was substantially higher. The combination of a small distance between randomly-selected authors and a large clustering coefficient relative to a randomly-connected network is often taken as evidence of a network being a 'small world'.15
Examining the distributions of quantities
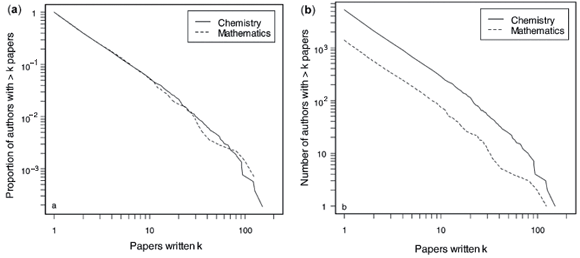
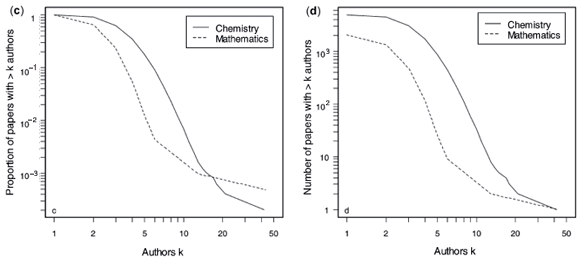
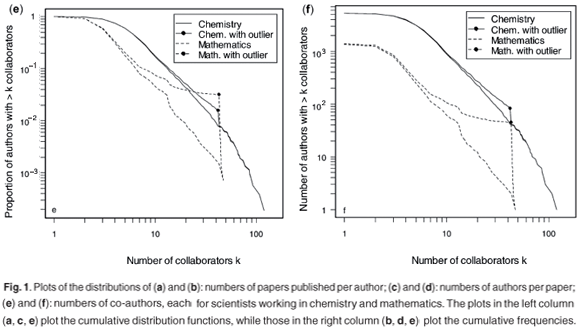
It is often of interest in analysing the statistical properties of networks to examine the entire distribution of a quantity, rather than just looking at the mean. Figure 1 shows the distributions of the number of papers published per author, the number of authors per paper, and the number of co-authors. Since all of these distributions show extreme positive skewness, we follow the convention of plotting them on logarithmic scales. Plots are given for both relative frequencies [the cumulative distribution functions contained in Figs 1(a), (c) and (e)] and absolute frequencies [in Figs 1(b), (d) and (e)]. Note that because of the larger size of the chemistry network and the logarithmic scaling, the cumulative distributions for the mathematics network do not extend as far toward zero as for those of the chemistry network.
The distributions of the number of papers written per author, shown in Figs 1(a) and (b), are essentially identical for the two networks over the vast majority of the domain, and the distributions are very similar, even in the extreme right-hand tail. The median number of papers published in both networks is just below two, and the 90th percentile is very close to six papers, again for both networks. Thus the similarities observed in Table 1 are in fact effective equalities of distributions, rather than just equality of means. The straight line followed by the distributions when plotted on logarithmic scales is suggestive of a power law distribution over most of the domain, a result first noticed by Lotka in 1926.16 In the extreme right tail, however, the distribution decays faster than a power law would dictate, requiring the addition of an exponential cut-off. This 'power law with an exponential cut-off' has also been identified in previous work,5 where it was suggested that an exponential cut-off was required to deal with the 5-year time horizon of that particular study, this being far shorter than a typical career time-span in research. That our exponential cut-off appears less clearly and further into the right-hand tail than it did in those earlier studies reflects the longer time period used in the current study, but remains consistent with the interpretation of compensation for a finite time horizon.
Figures 1(c) and (d) show that the main difference in the distributions of the number of authors per paper emerges in the early left-hand region of the domain, where the proportion of mathematics papers with just one or two authors far exceeds the proportion in chemistry. Nearly 35% of all mathematics papers are single-author publications, compared with just 8% for chemistry, and 42% of mathematics papers have two authors, compared with 29% for chemistry. These figures are extremely similar to results reported elsewhere for international publications.13 The greater relative proportion of mathematics papers containing extremely high numbers of authors should be taken with reservation, and it should be remembered that both of these right tails consist of a single observation (which receives greater weight in the smaller mathematics network).
Figures 1(e) and (f) finally show the distributions of the number of co-authors in each of the networks. In this case, the effect of the so-called 'outlier' papers—those consisting of many authors who generally do not appear again in the database—is sufficient to warrant showing the distributions both excluding and including these papers, where they appear in the latter as small solid circles. Their effect on the distributions of co-authors is not large in the chemistry network, due to the larger size of this network and the fact that there are several authors with substantially more co-authors than the number of authors in the outlying paper. The effect is far stronger in the mathematics network, which is both smaller and has only two authors with more co-authors than those authors making up the outlying paper in that network. In either case, it is clear that differences between the subjects exist in both the left- and right-hand parts of the distribution. Scientists in the mathematics network are more likely to have either no or a very limited number of co-authors, compared with those in the chemistry network. Nearly 8% of all authors in mathematics have no co-authors while a further 33% have just one co-author, compared to figures of 1% and 9%, respectively for scientists in the chemistry network. These figures are considerably smaller than those reported in Mouton11 —to the effect that 19% of projects in the chemical sciences and 48% of projects in the mathematical sciences are non-collaborative—but the sampling frame is entirely different in that study, mitigating against direct comparison of the results. Then, scientists in the chemistry network are also much more likely to possess extremely large numbers of co-authors. The maximum number of co-authors in the mathematics network is 47, while 35 authors in the chemistry network have more than this number of co-authors (the maximum is 119 co-authors). To a certain extent this reflects the relative sizes of the two networks, but there also appears to be evidence of meaningful differences in how research is carried out in the two disciplines. This is consistent with results reported in other studies.5,8,9
Network researchers have been particularly interested in the distribution of the number of co-authors, because a model of co-authorship in which new authors are more likely to work with those who have already extensively co-authored with others (called 'preferential attachment'17) results in a distribution of the number of co-authors that follows a power law. As pointed out by Moody,10 the importance of identifying preferential attachment and its consequent power law distribution, when it occurs, lies in its implied centrality of a small number of extensively collaborating scientists to the production and communication of knowledge. Both our outlier-free distributions clearly do not follow a power law over the whole domain, although it may be a reasonable fit to intermediate numbers of co-authors. The exponential cut-off in the right-hand tail is again evident, and is consistent with distributions of numbers of co-authors reported by several other authors.5,6,8,10 The lack of fit at low numbers of co-authors is also consistent with other studies,8–10 but is somewhat contrary to other degree distributions obtained in the sciences.5,6 However, it appears reasonable to say that preferential attachment is insufficient to fully explain the dynamics of the co-authorship networks, and that there are at least two other substantive processes at work.
Identifying the most productive and most collaborative researchers
We briefly examine two further topics in this, and the following section. Table 2 lists the most productive members of the two databases, according to the criteria of numbers of papers published and number of other co-authors. In both subjects, the most productive author of papers is not the same as the author with the most co-authors (here called most 'collaborative'). In fact, the author with the largest number of mathematics publications, Y. Yavin, has only 11 co-authors and does not even appear in the top 30 in the co-authorship list. The two sets of lists clearly illustrate both the dependence of an author's centrality in the co-authorship network on the number of papers written and the fact that the number of papers published is not on its own sufficient to describe network structure. Of the ten most collaborative authors in the chemistry network, six appear in the list of the ten most productive authors; five of the ten most collaborative authors in mathematics also appear in the most productive list. This observation reaches its extreme in the 42 authors who share fifth place on the list of most collaborative authors in mathematics: these authors co- authored a single paper but only one of them published any other papers. They are thus listed together as 'Other authors'b.
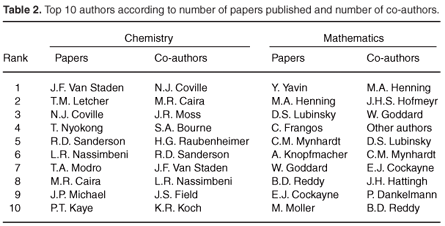
Close co-authorship networks
In this section we consider networks of authors who have co-authored more than three papers together. Recall that in the original networks, two authors are connected if they have been co-authors on a paper together. This, in a sense, was a working definition for collaboration between scientists. By increasing the number of co-authorships required from one to three, we place a more stringent requirement on the extent to which collaboration must have occurred before two scientists can be considered connected. We define the resulting networks as 'close co-authorship' networks for this reason. Table 3 shows relevant summary statistics for these close co-authorship forms of the chemistry and mathematics networks.
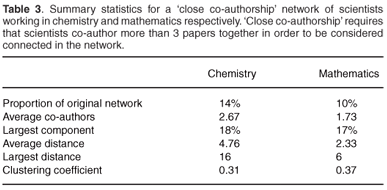
In both subjects, roughly 10–15% of authors are involved in one or more close co-authorships. Those scientists who form part of the networks have an average number of 2.7 close co-authors in chemistry and 1.7 in mathematics. It appears that the smaller number of co-authors observed in Table 1 for those in the mathematics network is therefore not due to those co-authorships being closer or more productive but is the result of some other difference in the way that research is carried out in this field.
Interestingly, the size of the largest component, which was far larger in the full chemistry network than the mathematics network, is nearly equal between subjects when the close co-authorship networks are used. This suggests that the chemistry research 'community' alluded to earlier is structured largely by numerous short-term partnerships and collaborations around a single or small number of papers. Otherwise, it appears that many of the structural features that exist in the full networks also prevail in the close co-authorship networks. The average distance between authors remains smaller in the mathematics network of close co-authors, and the clustering coefficient is very similar between the two subjects, since the 'outlying' mathematics paper containing 43 authors no longer contributes to the calculation of this statistic.
Conclusions and future research
We have used co-authorship networks in the preceding sections to investigate research involving South African scientists working in the fields of chemistry and mathematics. Co-authorship networks use mutual authorship of a paper as a proxy for collaboration, so that an analysis of the structure of the network provides information about the degree of inter-connectivity in the network, the nature (or perhaps 'shape') of this connectivity, and the relative positions of different people in the network. The data we used are from papers recorded in the ISI-citation indexes or papers in South African accredited journals between 1990 and 2005.
Scientists in both fields tend to produce very similar quantities of papers, and Fig. 1(a) shows that the distributions of the number of papers, per author, are nearly identical in the two fields. Chemistry papers, however, tend to have substantially more authors than mathematics articles. More than 75% of all mathematics papers have two or fewer authors, compared with only 37% of chemistry papers. Assuming that the absolute contribution of each author to a paper in terms of time and effort should probably decline as the number of authors on a paper increases, it is perhaps surprising that scientists in chemistry are not more productive than those in mathematics in terms of numbers of publications.
The larger number of authors on chemistry papers suggests that those working in chemistry will tend to co-author with a greater number of colleagues than those in mathematics. This is strongly supported by all results, showing that scientists in chemistry are both less likely to have very small numbers of co-authors and more likely to have extremely large numbers of co-authors. The latter finding may in part be due to the larger size of the chemistry network, but the former is surely predominantly due to fundamental differences in the way research is done in the two fields. These findings are consistent with previous research on co-authorship patterns, indicating the increase in numbers of co-authors as one moves from theoretical disciplines like mathematics to experimental ones like certain areas of chemistry.5,8,9,12 The relative isolation in which mathematicians work has also been highlighted by the unusually small size of the largest component in that network. In contrast to previous studies which found large- and similar-sized largest components across disciplines, we found that only 16% of authors formed part of the largest component in the mathematics network. This suggests that the South African mathematical research community may be more fragmented than most, although it is important to bear in mind that the implied isolation is only in terms of the co-authorship networks studied here. Of course, there may still be important sharing of work and ideas; it is just that if these are occurring they are not leading to collaborative publication.
Co-authorship networks provide an array of useful tools for investigating patterns of research and especially collaborative research. Our intention in this paper has been to take a first look at some of these results, but various possibilities for further analysis present themselves, including examination of the relationship between co-authorship and productivity, and examining inter-institutional co-authorship within the university sector in South Africa, as well as with other sectors (such as the science councils, national research facilities and industry). An equally important question concerns the countries with which scientists in these fields collaborate. Preliminary research conducted by CREST suggests that South African scientists across most fields have increased the extent of their international collaboration. However, most collaborations now seem to be with countries and regions outside Africa (the U.S., Europe or Australasia) with little collaboration with other African countries. Given the growing importance of South Africa as a regional leader in the field of science (we generate 80% of all science publications from SADC countries), it is imperative that collaboration with other scientists on the continent be actively encouraged.
We gratefully acknowledge Derick van Niekerk at the Centre for Research on Science and Technology at the University of Stellenbosch for providing us with the data.
1. Egghe L. and Rousseau R. (1990). Introduction to Informetrics: Quantitative methods in library, documentation and information science. Elsevier, Amsterdam. [ Links ]
2. Persson O. and Beckmann M. (1995). Locating the network of interacting authors in scientific specialties. Scientometrics 33(3), 351–366. [ Links ]
3. Pouris A. (2003). South Africa's research publication record: the last ten years. S. Afr. J. Sci. 99, 425–428. [ Links ]
4. Pouris A (2007). The international performance of the South African academic institutions: a citation assessment. Higher Education 54, 501–509. [ Links ]
5. Newman M.E.J. (2001). The structure of scientific collaboration networks. Proc. Natl Acad. Sci. USA 98(2), 404–409. [ Links ]
6. Newman M.E.J. (2001). Scientific collaboration networks. I. Network construction and fundamental results. Phys. Rev. E 64(1), 16131. [ Links ]
7. Newman M.E.J. (2001). Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 64(1), 016132. [ Links ]
8. Newman M.E.J. (2004). Coauthorship networks and patterns of scientific collaboration. Proc. Natl Acad. Sci. USA 101(suppl.1), 5200–5205. [ Links ]
9. Barabási A.L., Jeong H., Néda Z., Ravasz E., Schubert A., and Vicsek T. (2002). Evolution of the social network of scientific collaborations. Physica A: Statistical Mechanics and its Applications 311(3–4), 590–614. [ Links ]
10. Moody J. (2004). The structure of a social science collaboration network: Disciplinary cohesion from 1963 to 1999. Am. Sociol. Rev. 69(2), 213–238. [ Links ]
11. Mouton J (2000). Patterns of research collaboration in academic science in South Africa. S. Afr. J. Sci. 96, 458–462. [ Links ]
12. Moed, H. (2005). Did scientific publication productivity increase? In Citation Analysis in Research Evaluation. Springer. [ Links ]
13. Glänzel W. (2002). Co-authorship patterns and trends in the sciences (1980–1998). A bibliometric study with implications for database indexing and search strategies. Library Trends 50(3), 461–473. [ Links ]
14. Batagelj V. and Mrvar A. (2000). Some analyses of Erdös collaboration graph. Social Networks 22(2), 173–186. [ Links ]
15. Watts D.J. (1999). Small Worlds: the dynamics of networks between order and randomness. Princeton University Press, Princeton, NJ. [ Links ]
16. Lotka A.J. (1926). The frequency distribution of scientific production. J. Washington Acad. Sci. 16, 317–323. [ Links ]
17. Barabási A.L. and Albert R. (1999). Emergence of scaling in random networks. Science 286, 509–512. [ Links ]
Received 28 January. Accepted 16 October 2008.
* Author for correspondence. E-mail: ian.durbach@uct.ac.za
a Although SA Knowledgebase is a proprietary database of CREST, the final list of papers generated for the analysis presented in this paper can be made available (contact the first author).
b The same observations hold when looking at the entire networks: the correlation between number of papers published and number of co-authors is 0.73 and 0.26 in the chemistry and mathematics networks, respectively, when all authors are included. With the outlying paper in each network removed, the correlations are of course higher, rising to 0.80 and 0.70 respectively. The association is thus strong but far from perfect.