RESEARCH LETTERS

 

Parameter extraction from dark current–voltage characteristics of solar cells

 

 

Erees Q.B. Macabebe^‡; E. Ernest van Dyk

Centre for Energy Research, Department of Physics, Nelson Mandela Metropolitan University, P.O. Box 77000, Port Elizabeth 6031, South Africa

 

 

---

ABSTRACT

Electrical properties derived from the dark current–voltage (I–V) characteristics of solar cells provide essential information necessary in the analysis of performance losses and device efficiency. Device parameters of crystalline silicon solar cells were determined using the one-diode and two-diode models. The parameters extracted from the dark I–V curve of the solar cells were series resistance, shunt resistance, saturation currents and ideality factors. Iteration and approximation techniques were used to determine the device parameters of the solar cells. The method, which considered a finite shunt resistance in the high current region of the curve, made the implementation different from other techniques. Standard deviation, R² values and a fitting routine that provides a graphical representation of the output were implemented to determine the best set of parameters. Comparison of the extracted device parameters against the simulated values suggests that the two-diode model is more suitable than the one-diode model in describing the behaviour of the dark I–V curve. The two-diode model also provides more information necessary to explain the mechanisms governing the I–V curve under dark conditions.

---

 

 

Introduction

Studying the electrical characteristics of solar cells under dark conditions allows one to determine the device parameters and to predict the performance of the solar cell prior to deployment. The parameters derived from the dark current–voltage (I–V) characteristics can provide essential insights into the performance parameters which determine the efficiency of the device. The dark I–V curve is fitted into a model and the parameters of the model are determined to extract the electrical properties of the solar cells. Two established models were used in this study: the one-diode model, which considers the solar cell as a single p-n junction diode with parasitic resistances, and the two-diode model, which takes into account the recombination centres in the solar cell junction.

Several methods for parameter extraction from dark I–V characteristics using the two-diode model have been reported. One method¹ introduces piece-wise fitting to interpret the behaviour of the dark I–V curve. This entails division of the dark I–V curve into regions and fitting these into the model independent of the other regions. Another method^2,3 assumes that the shunt resistance is infinite in the high current region (HCR) where the series resistance dominates.

The extraction routine used in this study has made use of both approximation and iteration techniques. Unlike the methods mentioned above, the shunt resistance was assumed to be finite throughout the dark I–V curve in this implementation. Analysis of the behaviour of the dark I–V curve and the processes involved in the operation of the solar cells was made, based on the interpretation of the extracted parameters.

 

Theory

Under dark conditions, the current–voltage characteristics of a p-n junction solar cell with parasitic resistances at forward bias are represented by the equation:

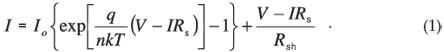
The series resistance R_s accounts for ohmic losses due to the bulk resistance of the semiconductor material and the metallic contacts. Current leakages across the p-n junction are represented by the shunt resistance R_sh. The ideality factor n provides information on the quality of the junction and the saturation current I_o is related to the properties of the semiconductor material found in the expression:⁴

The diffusion coefficients of electrons D_n and holes D_p depend on the mobility of the carriers through the semiconductor material. N_A and N_D are the densities of acceptors and donors, q is the electron charge, A is the area of the cell and n_i is the intrinsic carrier concentration. The finite recombination velocity of electrons and of holes, F_n and F_p, at the front and back surfaces of the solar cell depends on the physical and chemical states of the surfaces. It is highly affected by the influence of heavy doping and on injection carriers.⁵ The diffusion lengths L_n and L_p affect the saturation current of the p-n junction such that they should be long enough to guarantee that the generated carriers reach the contact areas of the solar cell before they recombine.⁶ The performance of the cell improves if the minority carrier diffusion length in the base region of the cell is greater than the thickness of the base.

The derivation of the one-diode model [Equation (1)] assumes that recombination in the space-charge region (SCR) is negligible. This, however, is not true in practical cases. Defects in the semiconductor can introduce traps allowing recombination of minority charge carriers in the SCR. Wolf et al.⁷ studied the effect of defects on the I–V characteristics of solar cells by subjecting them to proton radiation of 20–80 MeV at fluences of 1012–1015 cm^–2 to introduce recombination centres in the SCR. They reported that as the density of traps in the SCR was increased, recombination from these traps started to dominate the I–V characteristics of solar cells. The radiation resulted in a saturation current with an activation energy of half the bandgap energy, which is a characteristic of deep traps. The recombination current I_rec showed an exponential dependence given by⁸

The recombination saturation current I_SR is proportional to the width of the depletion region and inversely proportional to the minority carrier lifetimes. The ideality factor n_R should approximately be equal to 2. Since the dark I–V characteristic is a superposition of the two processes, diffusion and recombination, solar cells can then be modelled using the two-diode equivalent circuit shown in Fig. 1 with diodes D₁ and D₂ representing the diffusion and recombination processes, respectively.

 

 

The relationship between the applied voltage V and the current I is given by the equation⁷

The saturation currents I_o and I_SR and ideality factors n and n_R are the parameters associated with the two processes.

 

Program algorithm

Parameters of the one-diode model were extracted using a program that employed the iterative method.⁹ LabView was used to create a program that made use of a user-defined parameter initialization scheme to set the boundaries of the iteration and minimize computing time.

The algorithm used to extract the parameters (R_s, R_sh, I_o, I_SR, n, n_R) of the two-diode model utilized both approximations and iterative techniques. Approximations were made based on assumptions consistent with the theory. The behaviour of the curve in the HCR was considered to determine the parameters of diode D₁. The dark current I is much greater than the saturation currents I_o and I_SR in this region. Since n_R is greater than n, the second term in Equation (2) was assumed to be negligible. Assuming that I > I_o, Equation (2) is reduced to:

Isolating the exponential term and obtaining the natural logarithm results in the equation:

The parameters I_o and n were calculated from the slope and y-intercept of the linear regression plot of Equation (3). The initial value of R_sh was roughly estimated using the slope of the linear regression plot of the user-specified shunt region and, if necessary, was later refined by iteration to fit the model. The parameters R_s, n_R and I_SR were determined by iteration. Boundary conditions were set to limit the iteration range and ensure that the extracted parameters approximate the actual device parameters with minimal errors. One of these conditions is the tolerance percentage, tol%, which is based on the difference between the computed and the measured current. The tol% condition dictates whether an adequate set of parameters has been determined. The standard deviation value and R2 were used to determine the best fit curve.

Several dark I–V data with typical solar cell parameters were generated using Equation (2) to evaluate the accuracy of the two-diode parameter extraction program. An error of 0.1% was introduced during simulation to investigate how the algorithm would handle errors in the actual data. The simulated parameters were then extracted from the generated dark I–V data at different tolerance values. Figure 2 shows a sample generated and fitted dark I–V curve. When the extraction tolerance value was set to 0.1%, the resulting R² value is almost equal to 1. This means that at that tolerance percentage, the extraction program was able to determine a set of parameters that resulted in a curve fit identical to the measured I–V curve. The simulated and extracted parameters of the sample curve are listed in Table 1. The average percentage errors of the extracted parameters at different tolerance values were also studied. The smallest errors were achieved when the tolerance was set between 0.001–0.1%. It was also in this range that most of the fitted curves obtained an R² value equal to 1. When the tolerance was at 0.0001%, the average error was higher. This can be due to the error introduced to the generated data during simulation. At this tolerance percentage, the extracted parameters came closer to the 'pseudo-parameters' of the generated data, instead of converging to the values of the parameters indicated in the simulation program.

 

 

 

 

Extraction results

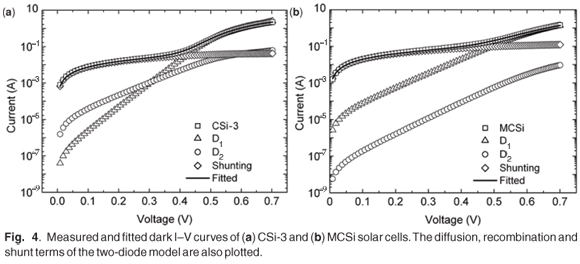
The dark I–V characteristics of one multicrystalline (MCSi) and four monocrystalline (CSi) silicon solar cells were obtained and the parameters of the two models were extracted using the methods presented. The extracted parameters of the five solar cells, the standard deviation and R² values of the fitted curves are listed in Table 2. The measured and fitted dark I–V curves of CSi-3, using the one-diode and two-diode model parameter extraction programs, are plotted in Figs 3(a) and (b), respectively. The curve fit using the two-diode model has a higher R² value and a lower standard deviation than the fit using the one-diode model. Figure 4 shows the measured and fitted dark I–V curves of (a) CSi-3 and (b) MCSi solar cells. The diffusion, recombination and shunt terms of the two-diode model are also plotted. The plots show that the recombination current D₁ and the shunt current overlap with the measured I–V in the HCR and the low current region (LCR), respectively. This means that D₁ dominates the HCR whereas shunting effects are more dominant in the LCR.

 

 

 

 

 

 

The relatively low R_s values (see Table 2) obtained from the five solar cell samples suggest that current losses are minimal, producing a steeper slope in the HCR. Except for CSi-2, the solar cell samples have very low shunt resistance, indicating high leakage current across the junction, which is the main contributor to the dark current. Analysis of the parameters extracted using the one-diode model gives us an overview of the general behaviour of the dark I–V curve. The parameters R_sh, I_o and n describe the curvature and slopes in the LCR, whereas R_s dictates the curvature of the HCR. Investigating the diode parameters, among the samples, CSi-1, CSi-2 and MCSi have idealities greater than 2. Kaminski et al.¹⁰ obtained dark I–V curves at various temperatures and determined whether a diffusion or recombination process dominated the solar cell's behaviour. An ideality factor as high as 5.5 was observed by the group. Idealities greater than 2 are attributed to recombination in the quasi-neutral region (QNR) due to trap-assisted tunnelling and field-assisted recombination. Another reason for the high ideality factors could be attributed to nonlinear contact resistance, which was not taken into account in the models. When the potential difference across the cell exceeds the thermal voltage (kT/q), the lump series resistance R_s in the model breaks down and the nonlinearity becomes apparent.^{11, 12} It is therefore possible that the resulting nonlinear series resistance at high voltages may have caused the increase in the ideality factors. Nonlinear series resistance can also be the reason for QNR recombination, which is predominant in CSi-1, CSi-2 and MCSi as signified by their ideality factors, whereas in CSi-3 and CSi-4, SCR recombination is the dominant mechanism.

The parameters of the exponential terms of the two-diode model indicate which of the processes govern the operation of the solar cell in the two regions of the curve. Since the extraction yielded low shunt resistances, this indicates that shunting dominates the solar cells especially in the LCR. The other parameters—saturation currents and diode ideality factors—provide the necessary information to explain the varying slopes of the LCR and the HCR, a prominent feature of the dark I–V curve. In CSi-1 and CSi-2, for instance, the high ideality factors (2.1–4.03) suggest that the dark I–V curves are characterized by QNR recombination. In CSi-3 and CSi-4, QNR recombination and SCR recombination govern the solar cells in the LCR and HCR, respectively. For the MCSi solar cell, n_R = 1.94 suggests SCR recombination in the LCR. However, the relatively high I_o value of 1.53 ×10^–5 A and n of 2.15 indicate that QNR recombination dominates the entire dark I–V curve. Plotting the diffusion, recombination and shunt terms of the two-diode model confirms the analysis made based on the extracted parameters. In Fig. 4(a), the high I_SR and n_R of CSi-3 shows QNR recombination represented by D₂ to dominate over SCR recombination in the LCR, whereas Fig. 4(b) shows that the current contribution of D₁ in MCSi is greater than that of D₂ throughout the dark I–V curve, as pointed out earlier. The magnitude of the dominant term in the LCR and in the HCR is the same as that of the measured dark current as demonstrated by the overlapping of the plots in Fig. 4. From the plots, we can see that the mechanism represented by D₁ dominated both devices in the HCR. Also, the effect of shunting is observed in the graphs as its plot overlaps with the measured current in the LCR. This indicates that for devices with low shunt resistance, the leakage current is the main contributor to the dark current in the LCR.

Comparing the two models, the two-diode model gave a better fit, judging from the standard deviation and R² values illustrated in Table 2. Also, the graphs shown in Fig. 3 confirm that the two-diode model yielded a better fit and is more suitable for describing the dark I–V characteristics of crystalline silicon solar cells because the parameters of the two exponential terms explain the behaviour observed in the graph.

 

Conclusion

The two-diode model best describes the behaviour of the dark I–V characteristics of crystalline silicon solar cells. This was demonstrated by the parameter extraction program and curve fitting routine described in this paper. Comparison of the standard deviation and R² values with the previous one-diode model parameter extraction program suggests that the two-diode model is more suitable and provides more information necessary to explain the behaviour of the curve and understand the processes governing the operation of the solar cells under dark conditions.

We would like to acknowledge the Schlumberger Foundation Faculty for the Future program for supporting E.Q.M., and the Nelson Mandela Metropolitan University for financial support.

 

1. Haouari-Merbah M., Belhamel M., Tobias I. and Ruiz J. (2005). Method of extraction and analysis of solar cell parameters from the dark current-voltage curve. In Proc. Spanish Conference on Electron Devices, Tarragona, Spain, pp. 275– 277.        [ Links ]

2. Kaminski A., Marchand J.J., Fave A. and Laugier A. (1997). New method of parameter extraction from dark I–V curve. In Conference Record of the 26th IEEE Photovoltaic Specialists Conference, pp. 203–206. Anaheim, CA.        [ Links ]

3. Radziemska E. (2005). Dark I-U-T measurements of single crystalline silicon solar cells. Energy Convers. Manage. 46, 1485–1494.        [ Links ]

4. Green M.A. (1982). In Solar Cells, chap 4, p. 81. Prentice-Hall, New Jersey.        [ Links ]

5. De S.S., Ghosh A.K., Sil D., Sinha P.K. and Bera M. (1995). Effect of surface recombination on the transit-time in heavily doped n+ -p junction silicon solar cell. Solid-State Electronics 38, 1270–1272.        [ Links ]

6. Tuominen E., Acerbis M., Hovinen A., Siirtola T. and Sinkkonen J. (1997). A method extracting solar cell parameters from spectral response by inverse Laplace transform. Physica Scripta T69, 306–309.        [ Links ]

7. Wolf M., Noel G.T. and Stirn J. (1977). Investigation of the double exponential in the current-voltage characteristics of silicon solar cells. IEEE Trans. Electron Devices ED-24, 419–428.        [ Links ]

8. Möller H.J. (1993). In Semiconductors for Solar Cells, chap. 2, p. 30. Artech House, Boston, MA.        [ Links ]

9. Macabebe E.Q.B. and van Dyk E.E. (2008). Extraction of device parameters from dark current-voltage characteristics of PV devices. Phys. Stat. Sol. (c) 5(2), 616–619.        [ Links ]

10. Kaminski A., Marchand J.J. and Laugier A. (1998). Non ideal dark I–V curves behavior of silicon solar cells. Solar Energy Mater. Solar Cells 51, 221–231.        [ Links ]

11. van der Heide A.S., Schönecker A., Bultman J.H. and Sinke W.C. (2004). Explanation of high solar cell diode factors by non-uniform contact resistance. Prog. Photovoltaics 13, 3–16.        [ Links ]

12. Pallarès J., Cabré R., Marsal L.F. and Schropp R.E.I. (2006). A compact equivalent circuit for the dark current-voltage characteristics of nonideal solar cells. J. Appl. Phys. 100, 084513.        [ Links ]

 

 

Received 18 March. Accepted 15 September 2008.

 

 

‡ Author for correspondence. E-mail: ereesqueen.macabebe@nmmu.ac.za