Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.9-10 Pretoria Sep./Oct. 2008
RESEARCH ARTICLES
A single-element plane-wave solid-state laser rate equation model
E.H. BernhardiI, II, *; C. BolligI; M.J.D. EsserI; A. ForbesI, II; L.R. BothaI; C. JacobsI, III
ICSIR National Laser Centre, P.O. Box 395, Pretoria 0001, South Africa
IISchool of Physics, University of KwaZulu-Natal, Private Bag X54001, Durban 4000, South Africa
IIIElectrical and Electronic Engineering Department, University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
ABSTRACT
A numerical rate equation model has been developed to describe the dynamics of a solid-state laser during continuous wave or Q-switched operation. The model allows the optimization of parameters such as the output coupler transmission percentage, crystal length and beam diameters, with the aim of improving the laser output performance. To validate the model, it was applied to a Nd:YLF laser, and proved successful in predicting and explaining the laser dynamics. It also satisfied our objective of creating a useful laser design tool.
Introduction
Diode-end-pumped solid-state lasers are very popular because of their high efficiency, excellent beam quality, compactness and robustness. With these desirable attributes, solid-state lasers have numerous applications in the medical, scientific, military and industrial fields. The ever increasing demand for laser applications ensures that the development of high-power diode-pumped solid-state lasers remains an active area of research. One of the most valuable tools that assists in laser design and construction is the use of mathematical models and simulations that explain and illustrate the operational principles of the laser.
In the next section we present a rate equation model that describes the dynamics of a diode-end-pumped solid-state laser during continuous wave (CW) or pulsed Q-switch operation. It is possible to make use of classical rate equations to describe a laser gain medium if the incident light exceeds the atomic transition linewidth.1
For the CW case, the rate equation model gives the output power and also predicts pulse energy, pulse peak power and pulse width for Q-switch operation. The model was developed to be general enough to model four-level and quasi-three-level lasers. In closing, we demonstrate the significance of the model by applying it to a four-level Nd:YLF laser, and show that there is very good agreement between the numerical model and experimental measurements. The model is useful in determining laser output as a function of parameters such as output coupler transmission percentage and crystal length.
The rate equation model
Energy-level population densities
The model as formulated here is applicable to an energy-level system as denoted in Fig. 1. This energy-level scheme is representative of four-level lasers. As a result of the electric field originating from the crystal host, the energy manifolds are split into discrete Stark levels.2 Making use of the effective absorption and emission cross sections ensures that the Stark-level splitting as well as the degeneracy of the energy levels are taken into consideration.
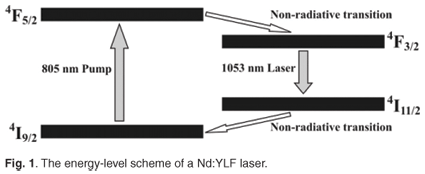
As the non-radiative transitions between energy levels (4F5/2 to 4F3/2 and 4I11/2 to 4I9/2) are very fast, we consider only two energy levels in this treatment of a four-level Nd:YLF laser, the upper laser level (4F3/2) and the ground level (4I9/2).3 The other two energy levels are assumed to be empty. Throughout this paper, we refer to the ground energy-level population density as N1, whereas the upper laser energy-level population density is denoted as N2. The total population density of active ions in the crystal is NT, so that

For the general case of a four-level laser, the rate equation for the upper laser level population density is defined as4–6
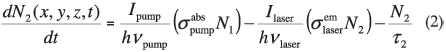
where Ipump is the total pump intensity in the standing wave resonator. A similar notation is used for the laser intensity. 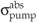 is the effective absorption cross section at the pump wavelength, while
is the effective absorption cross section at the pump wavelength, while 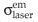 is the effective emission cross section at the laser wavelength and τ2 is the spontaneous emission lifetime of manifold level 2. From Equation (2), it follows that the number of active ions in level 2 will tend to increase due to absorption of the pump light (first term) and decrease due to stimulated emission (second term) and spontaneous emission (third term).
is the effective emission cross section at the laser wavelength and τ2 is the spontaneous emission lifetime of manifold level 2. From Equation (2), it follows that the number of active ions in level 2 will tend to increase due to absorption of the pump light (first term) and decrease due to stimulated emission (second term) and spontaneous emission (third term).
Laser photon distribution and number in the resonator
Let Ω be the total number of laser photons in the resonator. The laser light intensity is given by7
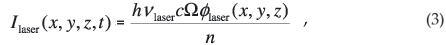
where υlaser is the frequency of the laser light, n the refractive index of the crystal and ølaser a normalized laser light distribution,
so that 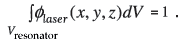
The time dependence of Ω can be described by4,7
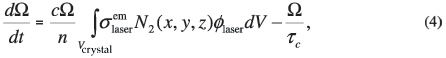
where 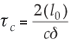 and l0 = lresonator + (n – 1)lcrystal (the corrected optical path), c the speed of light, and δ the logarithm of the round-trip loss. The round-trip loss includes general losses due scattering and residual transmissions of high reflectors as well as losses from the output coupler that transmits a fraction of the laser light. We assume that the losses in the resonator are small and that the output coupler transmits only a small fraction of the laser light (<10%), implying that the intensities of the laser light travelling in both directions in the resonator are roughly the same. Thus we assume that the laser power is equal at any given point inside the resonator. From these assumptions it follows that
and l0 = lresonator + (n – 1)lcrystal (the corrected optical path), c the speed of light, and δ the logarithm of the round-trip loss. The round-trip loss includes general losses due scattering and residual transmissions of high reflectors as well as losses from the output coupler that transmits a fraction of the laser light. We assume that the losses in the resonator are small and that the output coupler transmits only a small fraction of the laser light (<10%), implying that the intensities of the laser light travelling in both directions in the resonator are roughly the same. Thus we assume that the laser power is equal at any given point inside the resonator. From these assumptions it follows that
• 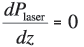
• 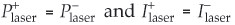 with the positive and negative signs referring to laser power travelling to the left and right, respectively, in the resonator
with the positive and negative signs referring to laser power travelling to the left and right, respectively, in the resonator
• 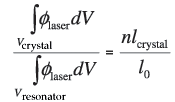
• ølaser 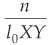 with X and Y being the transverse dimensions of the crystal.
with X and Y being the transverse dimensions of the crystal.
Single-element plane-wave assumption
The pump light that enters the crystal is usually highly non-uniform, which makes it necessary to set up the rate equations [Equations (2) and (4)] to be spatially dependent. However, in the single-element plane-wave approximation we assume that the pump light enters the laser crystal as a plane wave and is absorbed uniformly over the volume of the crystal. The transverse size of the crystal is assumed to be the same size as the pump beam, while the laser beam is assumed to have the same size as the pump beam. It follows from Equation (3) that Equation (2) now becomes
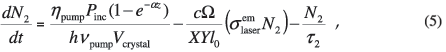
where ηpump is the pump efficiency (that is, the number of laser photons that are produced by each pump photon), α is the absorption coefficient, Pinc is the incident pump power and Vcrystal is the volume of the crystal. Since the population densities N2 and N1 are assumed to be constant over the volume of the crystal (single-element approximation), it follows that Equation (4) now becomes
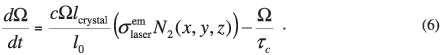
Equations (5) and (6) form the basis of the single-element plane- wave rate equation model.
Applying the model to a Nd:YLF laser
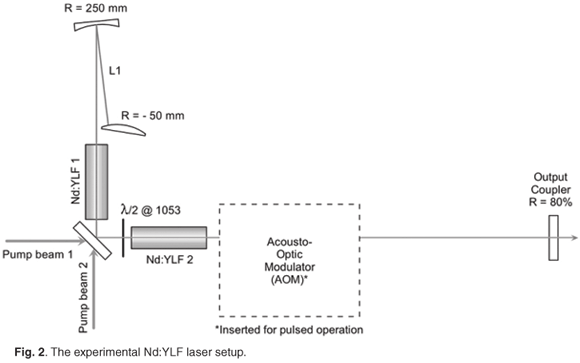
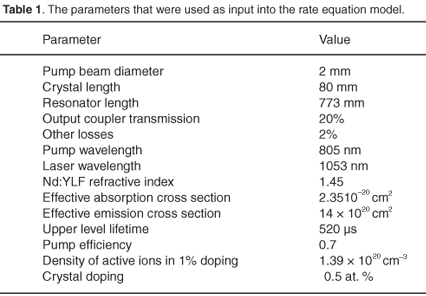
Experimental setup
The experimental setup of the Nd:YLF laser is illustrated in Fig. 2 and some laser parameters are listed in Table 1. A Jenoptik fibre-coupled diode module, capable of delivering a maximum power of 158 W at 805 nm, was used to pump the crystals. The fibre that was coupled onto the diode module had a 0.6 mm core. The high-power two-Nd:YLF crystal design required that the pump beam be split with a 50% mirror into two pump beams in order to pump the two crystals individually. For pulsed operation, an acousto-optic modulator (AOM) with a maximum loss of 65% was inserted into the resonator.
Modelling CW operation
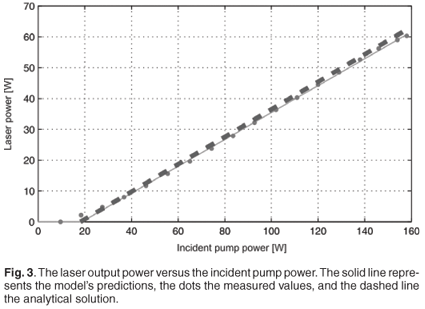
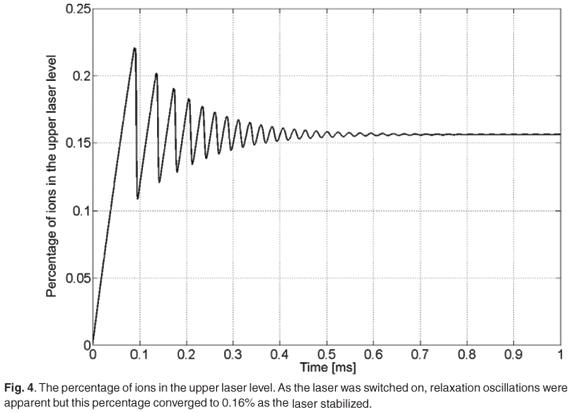
The derived rate equation model [Equations (5) and (6)] was implemented and solved numerically using Matlab's8 ordinary differential equation solvers. The laser parameters that were used as input into the rate equation model are listed in Table 1. These parameters were not adjusted in any way to fit the experimental data. For CW operation, the first step was to model the efficiency of the laser (output vs input power). The threshold of the laser was measured to be ~10 W, while an analytical solution according to Fan and Byer9 estimated the threshold to be 18 W. The model's prediction of 18 W agrees well with these values. At the maximum incident pump power of 158 W, the laser output power was measured as 60.3 W, whereas the model calculated the value to be 57.8 W (Fig. 3). An overall optical to optical efficiency was measured as 38%, whereas a slope efficiency of 44% was achieved. The analytical value10 for the slope efficiency was 48% and the rate equation model predicted a corresponding value of 44%. One main advantage of using the rate equation model instead of analytical solutions is that the population dynamics of the laser crystal can also be investigated (Fig. 4). When the laser was switched on initially, relaxation oscillations were apparent but as the laser stabilized, the percentage of ions in the upper laser level converged to a value of 0.16% of NT (at the maximum pump power of 158 W).
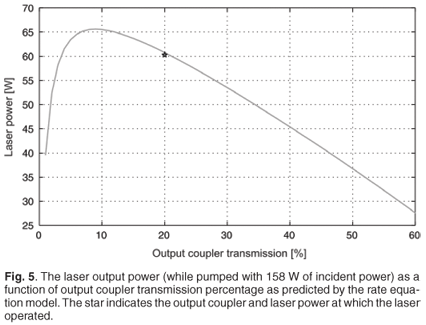
The output power dependence on the output coupler was also investigated. Figure 5 shows that the laser operated at an output coupler transmission of 20%, which produced an output power close to the optimal at an output coupler transmission of ~10%. Even though an output coupler transmission of this value produced a slightly higher laser output, we decided to build the laser with a 20% output coupler in order to reduce the power in the resonator to lower the risk of damaging any of the optics.
Modelling Q-switch operation
For Q-switched pulse operation, an AOM was placed inside the resonator to modulate the cavity loss. While the loss inside the resonator was high, stimulated emission cannot occur and the population density in manifold 2 increased. When the AOM loss was then decreased suddenly, the large population inversion resulted in a laser pulse. A repetition of this process resulted in a train of pulses.
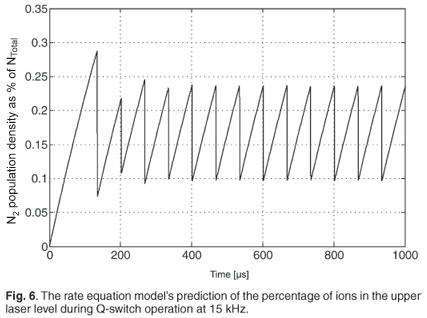
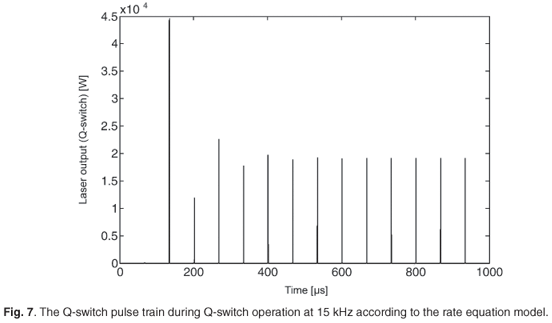
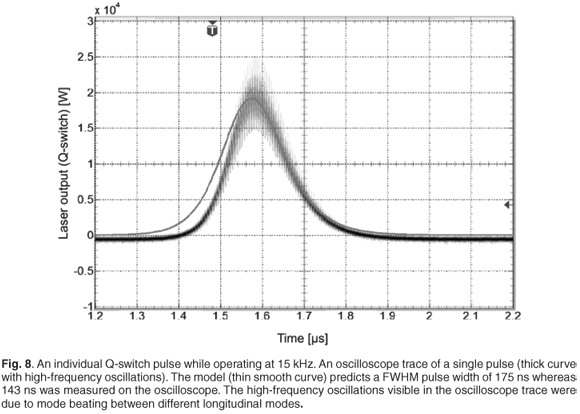
The first parameter that was investigated during pulsed operation was the population inversion (Fig. 6). Whereas the losses in the resonator were high due to the AOM, the population inversion increased from 0.097% to 0.236% as the laser could not lase and the gain kept increasing. As the losses then decreased, the population inversion changed suddenly from 0.236% to 0.097%, which produced a laser pulse. As the AOM modulated the losses in the resonator, a pulse train was formed (Fig. 7). A single pulse from this pulse train was selected to compare it with an oscilloscope trace (Fig. 8). At 15 kHz, the measured FWHM pulse width was 143 ns whereas the model predicted 175 ns. The high-frequency oscillations that were visible in the oscilloscope trace were due to mode beating between different longitudinal modes. The model produced a smooth pulse trace as it considered only a single longitudinal mode.
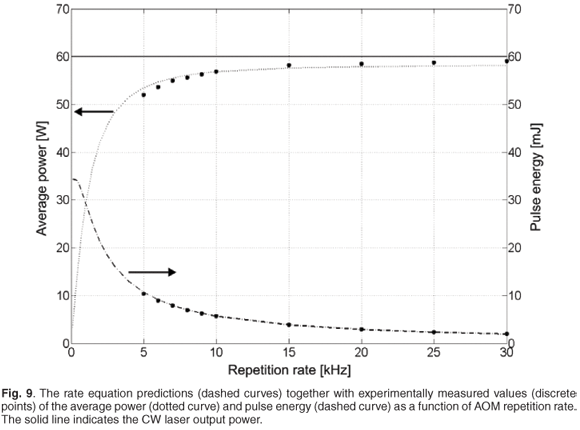
A further important analysis involved investigating the average power and pulse energy at various AOM repetition rates (Fig. 9). An average power of 59.1 W was achieved at 30 kHz, which decreased to a value of 52 W at 5 kHz. The pulse energy increased from 2 mJ at 30 kHz to 10.4 mJ at a repetition rate of 5 kHz. The model was in good agreement with these experimental results, especially at high repetition rates. Possible reasons for the slight deviation of the model at low repetition rates might be that the model has no spatial resolution and that up-conversion is currently being ignored. Unfortunately, no experimental results were available at repetition rates lower than 5 kHz, because one of the crystals fractured at 5 kHz.
Conclusion
A basic single-element plane-wave rate equation model was developed and applied to a Nd:YLF laser. The laser efficiency, output power and population inversion were among the parameters investigated. Comparison with experimental values showed that the model was successful in predicting and explaining the dynamics of the Nd:YLF laser during CW and Q-switch operation. The model proved also to be a very useful design tool for determining the optimal values of design parameters such as output coupling, crystal length and beam diameters.
1. Koudon R. (1994). The Quantum Theory of Light, chap. 2, pp. 80–81. Oxford University Press, Oxford. [ Links ]
2. Bollig C. (1997). Single-frequency diode-pumped solid-state lasers. PhD thesis, University of Southampton, U.K. [ Links ]
3. Koechner W. (1996). Solid-State Laser Engineering, chap. 1. Springer-Verlag, Heidelberg. [ Links ]
4. Fan T.Y. and Byer R.L (1987). Modeling and CW operation of a quasi-three-level 946 nm Nd:YLF laser. IEEE J. Quantum Electron. 23, 605–612. [ Links ]
5. Fan T.Y. (1992). Optimizing the efficiency and stored energy in quasi-three-level lasers. IEEE J. Quantum Electron. 28, 2692–2697. [ Links ]
6. Lim C. and Izawa Y. (2002). Modeling of end-pumped CW quasi-three-level lasers. IEEE J. Quantum Electron. 38, 306–311. [ Links ]
7. Rustad G. and Stenersen K. (1996). Modeling of laser-pumped Tm and Ho lasers accounting for upconversion and ground-state depletion. IEEE J. Quantum Electron. 32, 1645–1656. [ Links ]
8. Matlab (2007). Online at: www.mathworks.com/ [ Links ]
9. Fan T.Y. and Byer R.L. (1988). Diode laser-pumped solid-state lasers IEEE J. Quantum Electron. 24, 895–912 [ Links ]
Received 5 February. Accepted 16 June 2008.
* Author for correspondence. Present address: Integrated Optical Microsystems, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, Enschede, 7500 AE, the Netherlands. E-mail: e.h.bernhardi@ewi.utwente.nl














