Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.9-10 Pretoria Sep./Oct. 2008
RESEARCH ARTICLES
Enhanced efficiency of a parabolic solar trough system through use of a secondary radiation concentrator
P. Ferrer
School of Physics, University of the Witwatersrand, Private Bag 3, WITS 2050, South Africa. E-mail: philippe.ferrer@wits.ac.za
ABSTRACT
Solar electric energy is not yet economically competitive with fossil fuels. Apart from large capital outlay, solar systems suffer from low efficiency of converting solar energy to electric power. In this paper, a receiver for a solar trough was investigated in which the dominant radiation losses were suppressed by reducing the radiation area. The concentration ratio of the primary concentrator (a parabolic mirror) was enhanced by use of a simple secondary concentrator (an optical funnel), which minimized the width of the focal line. The resultant radiation losses were significantly reduced (by 22%). The novel aspect in this work was the design and modelling of a solar radiation receiver with secondary concentrator and black-body chamber. An initial model of this receiver showed an improvement of overall efficiency of about 1% for solar to electric power generation as compared to conventional receivers. Application of a receiver built on this model could reduce heat losses and costs of a solar trough system.
Introduction
The current worldwide trend is towards finding alternative energy sources. Looming difficulties in securing fossil fuels, their climbing costs together with their detrimental environmental impact all make it important to find viable alternatives, such as energy derived from biofuels, wind farms, wave and tide, nuclear, and solar. In South Africa, we are in an ideal position to exploit solar energy, with our regions of high solar irradiance and low yearly cloud cover.
There are many ways of extracting useful energy from the sun, ranging from domestic applications such as solar panels, flat-plate collectors, cookers, and pool heating systems to those of industrial size including power-towers (where the sun is reflected onto a central tower from a large number of mirrors surrounding it), solar troughs, and extensive assemblages of solar panels.
This article describes a solar trough system. Such systems consist of long, cylindrical parabolic mirrors and a similar length of pipe through which a 'working fluid' circulates (Fig. 1). The cylindrical trough-shaped parabolic mirrors produce a focal line (a focal point is produced only by circular parabolic mirrors) by concentrating the sun's radiation. The pipe runs along the focal line, absorbs the concentrated solar radiation and so is heated, thereby heating the working fluid inside it. The working fluid is then circulated to a power station where it is used to turn water into steam, which runs an electrical turbine.
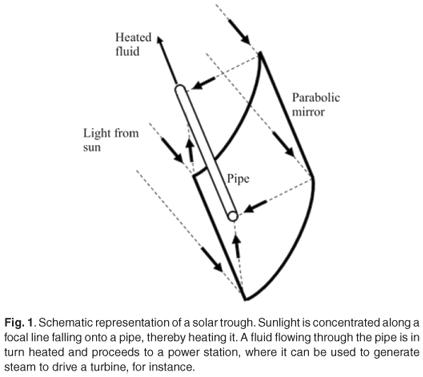
The solar trough is among the most-studied solar systems. The largest solar power plant in the world, the SEGS (Solar Energy Generating Systems) in California with a peak capacity of 364 MW, has been operational and studied in detail since the mid-eighties. The results of these studies have been sufficiently encouraging to warrant the subsequent construction of solar trough systems such as Nevada Solar One, with a capacity of 64 MW which went online in June 2007 (www.solargenix.com) and Andasol 1 in Spain.
At present, all solar technologies are economically inferior to those based on fossil fuels, largely due to their relatively low electrical conversion efficiency (~20% efficiency of converting solar radiation to electrical energy usable by the consumer) and high capital outlay.1 In order to make solar trough technology commercially more attractive, research is focused on improving materials by making them cheaper and more durable, and by increasing the efficiency of the solar plant. There are many ways of increasing the efficiency of a solar power plant, such as improvements in the optical system, reduction of heat losses from high temperature components and construction of heat storage facilities which can extend the operating time of the plant beyond sunset.
In this article, we concentrate on ways of reducing heat losses from high temperature components, especially the dominating one due to loss via radiation. Heat is lost along the hot pipe via convection, conduction and radiation. Convection and conduction losses are traditionally minimized by surrounding the hot pipe by an evacuated glass envelope. The vacuum between the pipe and the glass envelope cuts out convective losses, and conduction is reduced by using materials of low thermal conductivity. How to reduce both these types of losses is actively researched.
Radiation losses are reduced by painting the pipe with a selective coating,3 such as Solel-UVAC or Schott PTR-70 (www.schott.com), which have the property that they absorb solar radiation efficiently but emit infrared radiation, which represents the 'loss', very poorly, thus efficiently retaining most of the heat. This is a sensible way of reducing radiation losses, but unfortunately even the most temperature-resistant selective coatings break down thermally at around 400oC, thus restricting the maximum temperature at which a solar trough with these coatings can operate. Reducing the maximum operating temperature will reduce the efficiency of the overall power plant, since the efficiency of a heat cycle (such as is involved in obtaining electrical energy from steam) declines with decrease in operating temperature.
In the remainder of this article, a way is presented in which the radiation heat loss can be limited by reducing the area over which the loss occurs. The system studied consisted of a parabolic trough mirror (the 'primary concentrator'), which produced a focal line of concentrated solar radiation. The focal line was directed into a funnel-shaped mirror system (the 'secondary concentrator'), where the solar radiation was further concentrated and where it eventually fell on to and heated a pipe, which was inside a cavity (called a black-body chamber). In the following analysis, we review some fundamental ideas of solar engineering which concern us, but neglect other details such as the arrangement between primary and secondary concentrator, and also the issue of the selective coatings on the pipe. We first show how making the radiation loss area smaller will improve the efficiency of the overall system, then we derive an expression for the width of the focal line and how a secondary concentrator affects it. We then optimize the system such that it will operate at minimum loss and show that we can reduce radiation losses by about 22% compared with a system without a secondary concentrator. We further propose the design of a receiver based on the foregoing results and present some results from a performance simulation.
Area reduction and Carnot cycle efficiency
The Carnot cycle is used as the standard for comparison throughout this paper, although, depending on the system, other cycles may be more appropriate (such as the Rankine cycle, which is used in studying steam-powered electricity generation).
Consider the equation describing radiation heat flow,

where ε is the absorption/emission coefficient, σ is the Stephan-Boltzman constant, A is the radiation area and T2 and T1 are the body and surrounding temperatures, respectively. Radiation loss can be reduced via ε as is done using selective coatings on the radiation receiver, by reducing the temperature difference between the surroundings and the heated body, or by limiting the area which radiates.9
Reducing the area by an amount β (0 < β < 1) will reduce the radiation loss. We considered an object as described by Equation (1) , losing heat via radiation (we ignore any incoming radiation, i.e. T1 = 0), and the equation describing the heat loss is

We now compare Equation (2a) with Equation (2b), which describes an object with the area reduced by an amount β but losing the same amount of heat:

For the same heat loss Q, the temperaturewil T2' will be higher. The relationship between temperatures T2 and T2' is

In the case of the solar trough, this implies that with a reduced area, the receiver operates at a higher temperature, which in turn will elevate the temperature of the working fluid running through a pipe inside the receiver by roughly the same amount. A working fluid at higher temperature will be able to run the Carnot cycle, which is used to convert the heat energy to electrical energy at a higher efficiency. Carnot cycle efficiency, which measures the maximum possible efficiency of a heat engine operating between temperatures Tlow and T2, is given by

Assuming the raised temperature of the pipe inside the receiver increases the working fluid by a similar amount, the Carnot efficiency of a reduced radiation area increases to

Figure 2 illustrates the effects of area reduction on Carnot cycle efficiency. The temperature of the low-temperature reservoir was taken as 398 K. It should be noted that the analysis represented by Fig. 2 takes only radiation losses into account, and neglects the smaller losses due to convection to the surrounding air and conduction through the insulation material.

The collection area of the receiver will both receive solar and lose infrared radiation. The receiver needs to absorb a maximum amount of solar radiation via a minimum area. The minimum area in turn is restricted by the size of the focal line (the thinner the focal line, the smaller the receiver area needs to be and the greater the efficiency). Let us therefore review the theory behind the minimal width of the focal line, which will be useful in the design of the receiver.
Width of the focal line of a parabolic concentrator
Figure 3 depicts a cross section of a cylindrical trough parabolic mirror. For simplicity, the incident solar rays arrive nearly perpendicular to the line EF. These rays originate from the extremal points of the sun's disk (top and bottom rays of the sun's disk). The focal line is finite in width6 (DD' in Fig. 3) because it projects the image of the sun's disk (which is not a point). The angle subtended by the sun as seen by an observer on earth is about half a degree. From this, we derived a theoretical expression for the width of the focal line and the concentration ratio (see below).
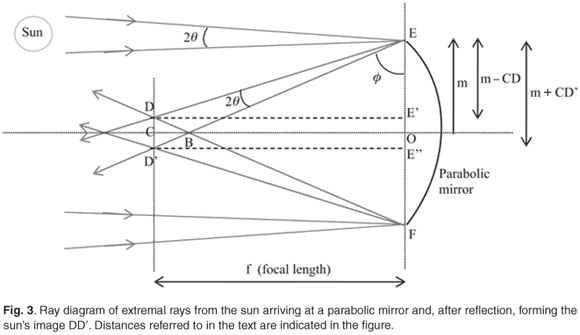
Using the constructed triangle EE'D and EE"D', we obtained the expression

which, by eliminating OB + CB, solves to

where we made use of CD = CD'.
The ratio m/CD is called the concentration ratio, which is the ratio of the area which collects sunlight (collector area) over the area into which the sunlight is concentrated (receiver area). The maximum concentration ratio can be obtained by differentiation of (6)

and is computed to be m/CD = 107 for ø = 45°.
Figure 4 shows that, at most, 107 'suns' (sun intensities) can be projected into a conventional receiver using a primary concentrator alone.
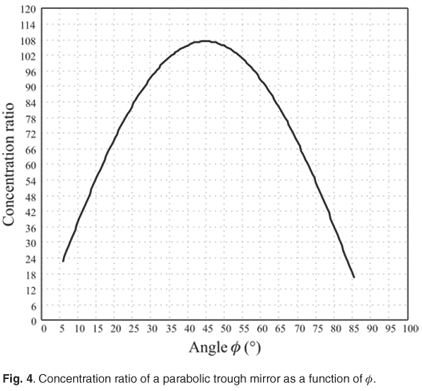
Conventional trough systems, such as that represented by SEGS, have typical concentration ratios1 of about 50–80. Decreasing the width of the focal line improves the concentration ratio and allows for a smaller receiver area, which loses less radiation.
The theoretical maximum for the concentration ratio of the best possible linear concentrator system is around 220,8 using any conceivable method of concentrating the radiation. Hence, in practice, there should be a way roughly to double the maximum concentration ratio shown in Fig. 4 with an additional optical system.
The optical funnel
The preceding section showed that there is an upper limit to the possible concentration ratio of a parabolic mirror on its own. The concentration ratio could, however, be improved by the use of a secondary concentrator, which further concentrates the already concentrated solar radiation coming from the parabolic trough mirror.
The idea of V-shaped mirrors to funnel light has been investigated by various authors.5–7 Studies for a solar trough using a compound parabolic concentrator (CPC) have been conducted chiefly by Winston.8 The funnel system is an approximation to the better-performing CPC, but is simpler and cheaper.
The idea of an optical funnel is basic and I briefly present it, because we will use the results in the following section. We employ a ray-tracing construction: in Fig. 5, a light ray enters the funnel opening y1 from the top and is reflected off the mirrored funnel wall at an initial angle of ø1 relative to the wall (1st reflection). The angle the funnel makes with the vertical is denoted by θf. The ray then penetrates a distance l1 into the funnel before reflecting off the opposite wall (2nd reflection), where the funnel distance is reduced to y2. It can reflect again to penetrate deeper into the funnel, repeating the process.
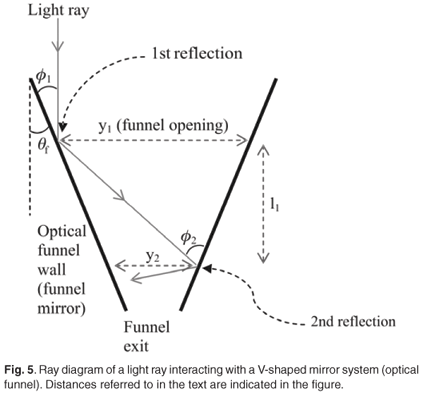
The calculation of the parameters of importance to describe this simple process, namely, yn, ln and øn, is done iteratively, once θf, y1 and ø1 are known.
The general expressions for ln and yn+1 after n reflections are5–7
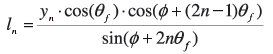
and

The total penetration of the ray can be computed from  after n reflections.
after n reflections.
The light ray's incident angle at the funnel wall becomes 'shallower' (closer to the horizontal) with each reflection and after several reflections will no longer be able to penetrate further into the funnel, but instead is reflected back out to the funnel opening whence it came. The maximum number of reflections that a funnel can sustain is obtained from the constraint that once the light ray is reflected parallel to the horizontal (or sloping slightly upwards in Fig. 5), then the subsequent reflection will reflect it even further upwards towards the funnel opening.
We want to obtain a concentration ratio for the funnel, again using the ratio of the incoming radiation area (the funnel opening where the light comes in) to the outgoing radiation area (the funnel exit at the bottom where the light exits); in other words, the initial funnel opening to funnel exit dimension y1/yn. In this context, it is convenient in order to simplify later calculations to define the functions

and

which are the factors multiplying the distances yn and ln, respectively, in Equations (8). The concentration ratio y1/y2 after n reflections can be expressed by eliminating ln. This gives

and an average mirror reflectivity j(0 < j < 1) has been assumed. The average mirror reflectivity is a measure of how much light is lost due to imperfections of the funnel mirrors, which are not perfect reflectors. Even if the funnel sides were perfect reflectors, the maximum concentration ratio for a V-shaped concentrator does not exceed 4 by much, and it is therefore not well suited as a primary concentrator, but useful in assisting a primary concentrator as in the present case.
The attractiveness of using this funnel lies in its ease of construction, maintenance and cheapness. In practice, a convenient arrangement would be two reflecting surfaces of polished thin aluminium plates in a funnel arrangement.
We next consider how to integrate the funnel with the primary parabolic mirrors.
The combined system of primary and secondary concentrators
The parabolic trough mirror and the optical funnel can be combined such that the concentration ratio of the overall system is increased.
We considered a system where a parabolic trough focused light into a funnel. The crucial condition is that the width of the focal line (DD'), as shown in Fig. 3, must equal the funnel opening y1 in Fig. 5, so that all the light coming from the parabolic mirror is transmitted into the funnel. We must further ensure that all the light leaves through the funnel exit and is not reflected back out through the funnel opening. At the funnel exit is a black-body chamber with a pipe, which absorbs the concentrated sunlight and increases in temperature (Fig. 6).

We will consider the case of one reflection for the funnel because any additional reflections will reduce the incident radiation as the mirror on the funnel walls is not a perfect reflector, and second, the improvement using two reflections is not significant.
In Fig. 6, we considered again the extremal rays entering the funnel, namely those originating from the rim of the mirror. If these exit through y2, then all other rays reflected by the funnel mirror will also exit through y2. The 'Inner ray' and 'Outer ray' originate from opposite sides of the sun's disk and are reflected off the parabolic mirror. We next calculated the opening distance y1 of the funnel such that all the sunlight reflecting off the parabolic mirror enters through it. As mentioned above, the opening needs to be the width of the focal line, and can be derived by considering the triangles ABE and ACE. The result is

in terms of the distance d of the parabolic mirror from the funnel.
The angle ø' can be related to the parabolic mirror angle ø via

where ø' is the ray entry angle into the funnel.
These expressions allowed us to obtain the penetration depth into the funnel, since we knew the funnel opening distance and the incident ray angle.

The expression for the dimension of the funnel exit dimension is

We were then able to compute the concentration ratio for the combined system, which is the product of the concentration ratios of the parabolic mirror and the funnel system, as a function of the angles ø and θf:

where we have set j = 1 (this assumes perfect reflection off the funnel walls and is a reasonable, simplifying approximation within this context).
Optimization of the combined concentration ratio
We wanted to obtain a result for the highest possible concentration ratio of the combined system. The solar disk angle is given in the literature by 2θ = 9.2 ×10–4 radians. The concentration ratio for the parabolic mirror, Equation (15), is a function of the angles ø and 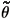 f. The maximum is found via
f. The maximum is found via

and occurs at ø = 52.6° and θf = 12.3°.
The new graph of incident angle f plotted against the total concentration ratio is shown in Fig. 7. The maximum concentration ratio is now found to be approximately 132.

The receiver
The previous discussion forms the basis of the novel design and modelling of a solar radiation receiver (Fig. 8). We will here merely outline our proposal, since the emphasis of this communication is on the optimization of the interplay between the primary and secondary concentrators and the benefits.

The receiver consists of a glass cover, behind which an optical funnel is mounted that channels the radiation into a black-body chamber, where the working fluid is heated inside a pipe. This receiver is more complex than the pipe and evacuated glass envelope used at SEGS, giving rise to different types of conduction and convection losses, which need to be taken into account. Losses include Q1, the conduction loss through an insulator at the back of the chamber; Q2, the radiation loss from the black-body chamber; and Q3 and Q4, the radiation and convection losses from the glass cover, respectively. A working fluid flows though a pipe inside the chamber, carrying away heat to a power station.
Figure 9 shows the results of an efficiency evaluation for a conventional receiver and a receiver with funnel, both without selective coating. 'Efficiency' here refers to that of the combined system of the receiver (solar collection) and the Carnot cycle (steam power generation). The efficiency is plotted against receiver length (Distance), which is heated by the parabolic mirror. The receiver with funnel shows an improvement of roughly 1% in efficiency. The peak efficiency of the receiver is about 28%, which compares favourably with the figure quoted for SEGS (~20%), but many more factors (such as parasitic losses through auxiliary electrical systems and the effective efficiency of the steam cycle, for instance) need to be taken into account before a direct comparison is realistic. Further, the length of the receiver pipes required to achieve this efficiency is longer than for the same receiver with a selective coating (such as SEGS) and it is therefore economically inferior. The use of radiation-reducing coatings, which has not yet been considered for this application, would certainly improve efficiency.

Conclusion
We have argued that reduction of the collection area of a solar receiver can be used to suppress the dominant radiation loss effects. A decrease in area led to a rise in temperature of the working fluid. This in turn increased the Carnot cycle efficiency. The reduction of area on conduction and convection does not greatly improve the Carnot cycle efficiency. We can therefore expect the overall efficiency to be somewhat less than that predicted by Fig. 2, in the region of 1% to 2%, as was seen in the receiver comparison (Fig. 9). To put this in perspective, an improvement of this order would be able to supply electricity to an additional 5000–10 000 people currently served by SEGS.
We next calculated the expected width of the focal line. In practice, the focal line will be wider than the theoretical prediction, due to manufacturing imperfections in the mirrors and structure. Nevertheless, by comparison with similar systems, we expect some 90% of incident radiation can be captured by the receiver. We then presented the theory describing the optical funnel and showed how to combine the parabolic mirror with the optical funnel to reduce the width of the focal line. We further optimized the expression for the total concentration ratio and found the optimum angles at which the concentration ratio is a maximum (and the receiver area minimized). The new maximum concentration ratio was found to be around 132 (up from 108 for a parabolic mirror without funnel), which represented a 22% increase in the concentration ratio or, equivalently, a reduction of receiver area by that amount.
Our discussion of a solar receiver based on the results of the integration between primary and secondary concentrators included an analysis of the conduction and convection effects. Computer simulations of efficiency comparisons between a receiver with and without a funnel showed that the funnel-type receiver performs about 1% better, but is open to improvements: the increase in efficiency is very sensitive to the parameter j, the average reflectivity of the funnel mirror, which for the simulations was set at 0.9, whereas more realistically it is closer to 0.95.
A detailed analysis of the receiver is still in hand, as there are many design parameters which can be optimized. Aspects which must still be investigated include the geometry of the black-body chamber, coatings inside the chamber and on the glass cover, use of different working fluids and different geometric arrangements for the receiver and parabolic mirror.
The analysis presented in this paper has shown the efficiency of the proposed receiver to be competitive with alternative systems.
I thank Laveshan Nayager for his contributions to this analysis.
1. Sargent and Lundy (2003). Assessment of Parabolic Trough and Power Tower Solar Technology Cost and Performance Forecasts, Subcontractor Report, SL-5641, prepared for the U.S. Department of Energy and National Renewable Energy Laboratory, Chicago, Ill. [ Links ]
2. Zimmer V.L., Woo C. and Schwartz P. (2006). Concentrated Solar Power for Santa Barbara County: Analysis of High Efficiency Photovoltaic and Thermal Solar Electric, ERG 226. [ Links ]
3. Price H. and Kennedy C. E. (2005). A progress in the development of high temperature solar selective coating. In Proc. ISEC2005 2005 International Solar Energy Conference, August 6–12, 2005, Orlando, Florida. [ Links ]
4. Duffie J.A. and Beckman W.A.(1991). In Solar Engineering of Thermal Processes, chap. 7. Wiley-Interscience, New York. [ Links ]
5. Williamson D.E. (1952). Cone channel condersor optics. J. Opt. Soc. Am. 42, 712. [ Links ]
6. Witte W. (1965). Cone channel optics. Infrared Physics 5, 179–185. [ Links ]
7. Kiatgamolchai S. and Chamni E. (in press). Theory and experiment of a two-dimensional cone concentrator for sunlight. Solar Energy. [ Links ]
8. Collares-Pereira M., Gordon J.M., Rabl A. and Winston R. (1991). High concentration two-stage optics for parabolic trough solar collectors with tubular absorber and large rim angle. Solar Energy 47, 457–466. [ Links ]
9. Welford W. T. and Winston R. (1978). The Optics of Nonimaging Concentrators. Academic Press, New York. [ Links ]
Received 18 March. Accepted October 2008.














