Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.9-10 Pretoria Sep./Oct. 2008
RESEARCH ARTICLES
The role of frictional stress on the generation of misfit dislocations
William A. Jesser*
Department of Physics, University of Pretoria, Pretoria 0002, South Africa
ABSTRACT
The concept of misfit strain driving dislocations to an interface between two different phases leads to a residual strain that is not accommodated by the misfit dislocations. The residual strain occurs when the misfit stress is reduced to a value insufficient to generate further misfit-accommodating dislocations at the interface. This idea has been applied to epitaxial films to account for the relaxation of strain with increasing film thickness. It is here extended to the case of endotaxial interfaces between a solid matrix and precipitate. This paper builds upon work of Nabarro published in 1940 and the frictional stress to be overcome to move dislocations into the interface.
Introduction
In this article, two early ideas of F.R.N. Nabarro are combined to introduce a new view of strain relaxation in endotaxial phases. The first idea was one of Nabarro's earliest contributions, a calculation of the strain energy of a misfitting sphere.1–3 The second idea, a later contribution of Nabarro's, was a calculation of the Peierls stress4 on a dislocation, later to be known as the Peierls–Nabarro stress.5 By minimizing the sum of the strain energy of a misfitting sphere and its interfacial energy between matrix and inclusion, one may calculate an equilibrium configuration of the system which includes misfit dislocations at the interface to accommodate the misfit and relax the strain energy. The focus of this article is on the energy barriers that inhibit achieving the equilibrium configuration as a general consideration and the role of the Peierls–Nabarro frictional stress in particular.
There are several mechanisms by which strain relaxation in the inclusion may occur. Weatherly has shown that prismatic dislocation loops may be 'punched out' to relax the strain when the misfit between sphere and matrix is above about 5%.6 If the inclusion forms at elevated temperatures, it was recognized that in order to reduce the natural misfit, point defects may collect at the interface, thereby enlarging or reducing the cavity in which the inclusion forms.7,8 In the present paper, the concept of Matthews and co-workers9–11 developed for epitaxial films will be applied to endotaxial inclusions. Matthews showed that threading dislocations move into the interface under misfit stresses to become misfit-accommodating interfacial dislocations, which also relax the film stress. The same concept applies to endotaxial inclusions when pre-existing dislocations are attracted to the interface to relax the misfit. While this concept has been presented before,8,12 what is new is introducing the role of a frictional stress in the mechanism of misfit dislocation generation to show that equilibrium may be inhibited when the driving, misfit stress drops to the level of the frictional stress. The introduction of a frictional stress that inhibits the motion of pre-existing dislocations has been applied to thin films13–18 to show that a residual strain exists even for very thick epitaxial overgrowths. In this paper, this notion will be applied to endotaxial inclusions to show the same effect as for thin films, namely, the achievement of full stress relaxation can be inhibited and a residual stress and strain remain even in large inclusions.
Several mechanisms for inhibiting the complete relaxation of stress in inclusions will be presented. First, the strain energy of the inclusion and the interfacial energy of the inclusion/matrix interface will be developed from the theories of Nabarro1–3 and van der Merwe,19–21 including the contribution from chemical bonding.22 For purposes of illustration of the principles involved, the simplicity of a spherical inclusion of an f.c.c. crystal of one atomic volume in an f.c.c. matrix having a different atomic volume from that of the inclusion will be assumed. From these beginnings, the equilibrium state that minimizes the sum of strain energy and interfacial energy will be shown as a function of size of the inclusion, and then the lack of achieving the equilibrium state as a result of energy barriers will be presented.
Equilibrium energy considerations
The equilibrium state is derived by minimizing the sum E of the interfacial energy Ei and elastic strain energy Es of inclusion plus matrix. Assuming the elastic constants of the matrix and inclusion are equal and denoting the shear modulus as G, Poisson's ratio as ν, the magnitude of the Burgers vector of the misfit dislocations as b, and the unstrained radius of the spherical inclusion as r, one may write12
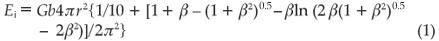
with

and the misfit fo in terms of the difference between nearest-neighbour distances a of inclusion and matrix given as

Here the subscript o denotes an unstrained value. The first term in brackets, 1/10, is an estimate of the bonding energy between inclusion and matrix and is taken as independent of small strains.22 Following Nabarro's strain energy calculations1–3 for the strain energy of a spherical inclusion of unstrained radius (1 + δo)r derived by transforming a spherical volume of matrix of unstrained radius r, one writes the total strain energy of distorted matrix and dilated (δo < 0) or compressed (δo > 0) inclusion as

The unstrained radius of the cavity in the matrix is r, but when the inclusion of unstrained radius (1 + δo)r is fitted into this cavity, the strained cavity radius and strained inclusion radius both become (1 + ε)r. This corresponds to a hydrostatic strain in the spherical inclusion of δ – ε for small strains. The matrix is dilated by a strain e which decreases with radial distance from the interface of the inclusion. Nabarro showed that

where K is the bulk modulus of the inclusion. In Nabarro's calculations, the inclusion and matrix are bonded across the interface, so that there is rigid atom to atom correspondence, that is, the interface is coherent and Ei = 2Gbπr2/5. However, the calculations of elastic strain energy would hold equally well for a non-coherent interface. The situation of a non-coherent interface can be modelled by introducing as variables the misfits f and d that depend on the degree of relaxation of interfacial coherency. These variable misfit parameters are related to one another by

where the energy expressions (1) and (4) describe the relaxed situation when fo and δo are replaced by f and δ, respectively. The use of Equation (6) allows one to write the energy sum E = Ei + Es in terms of one misfit variable, either f or δ, as shown in Fig. 1, which shows schematically how E varies with interfacial misfit f. The coherent interface corresponds to f = 0 (δ = δo) and the completely relaxed inclusion (non-coherent interface) to f = δo (δ = 0). A completely relaxed inclusion is one that resides in an unstrained matrix cavity that has the same size as the unstrained inclusion; e.g. in the case of an oversized inclusion (δo > 0), vacancies can migrate from the matrix to the interface to enlarge the cavity.7,8
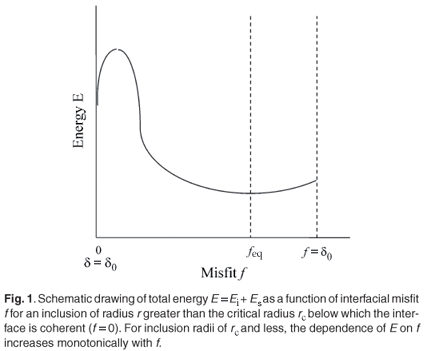
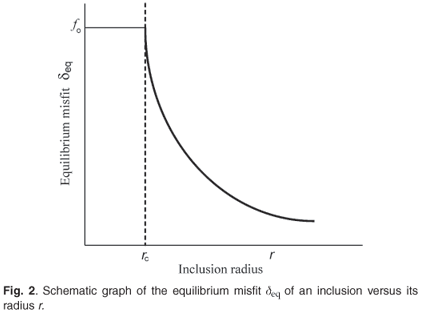
There exists a critical radius rc below which the equilibrium state is a coherent interface, so Fig. 1 is drawn for the case r > rc. As r increases, the equilibrium misfit at the interface feq increases and the corresponding inclusion misfit δeq decreases in magnitude. The equilibrium state which minimizes the energy sum E is represented in Fig. 2, which shows schematically the value of the equilibrium misfit δeq of the inclusion as a function of its size r. Analytically, the equations that describe the behaviour shown in Fig. 2 are available in the literature.12 The expression for rc is approximated by equating the interfacial energy Ei [Equation (1)] evaluated at δ = 0 (i.e. f = δ) to the misfit strain energy Es [Equation (4)] evaluated at δ = δo to yield
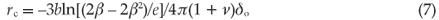
and
δeq satisfies ∂E/∂δ = 0
and is given by
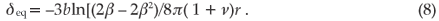
Mechanisms of stress relaxation
There are a number of ways a misfitting inclusion can relax the stress. The first one, already mentioned, is by accumulation at the interface of vacancies or interstitials for δ positive or negative, respectively.7,8 The cavity in the matrix is thus enlarged or reduced to relax the elastic strain energy but correspondingly there is an increase in the interfacial energy when coherency is lost. The interface loses coherency through the accumulation of geometrically necessary interfacial dislocations that form spontaneously when the matrix cavity changes its size. Figure 2 shows the equilibrium misfit that should be achieved in this way and one can see that only for large inclusions will this mechanism lead to negligible misfit at equilibrium. There is, however, a practical complication associated with this mechanism. Essentially, complete relaxation of the misfit, δeq = 0, is impractical because one expects point defect migration to the interface to be effective only at elevated temperatures. If the equilibrium misfit is reduced essentially to zero at the elevated temperature, then when the temperature is returned to room temperature a stress and misfit develop as a result of differential thermal contraction and the inclusion is left with a small residual misfit.
A second mechanism, prismatic dislocation loop punching, leads to a dislocation loop punched out into the matrix and a companion loop of opposite Burgers vector left at the interface. This loop pair relaxes the inclusion strain energy and increases the misfit dislocation density at the interface. While it should follow the energy minimization depicted in Fig. 2, more importantly it is only effective at high misfits where δ ~ 0.05.6
Once the misfit drops below this critical value for dislocation loop punching, the mechanism ceases to operate, leaving a residual misfit that is perhaps the largest of all the possible mechanisms for stress relaxation of the inclusion.
The final mechanism to be considered here is that of attracting pre-existing dislocations to the interface through glide and climb. The climb mechanism is just a modification in detail of the point defect accumulation mechanism discussed first. One can add here that there exists an energy barrier to point defects being absorbed by the dislocation23 and hence this barrier will result in a residual stress. The glide of dislocations to the interface to relax the strain energy at the expense of increasing the interfacial energy is subject to the geometrical requirement for misfit accommodation given by the relation

where be is the misfit-accommodating component of the Burgers vector b and is given by that projection of the interfacial normal n which is in the interface and normal to the dislocation line y. This relation shows that if a small dislocation loop were to exist at the interface with a Burgers vector such that one part of it is attracted to the interface to accommodate misfit, then the diametrically opposite part of the dislocation loop would be repelled from the interface as it would increase the misfit locally. This occurs because y changes sign on the opposite side of the loop and hence so does be. When the loop is near the equator of the inclusion, n and y both change sign across a diameter and be does not change sign. The result of this misfit accommodation by the component be can lead to the attraction of part of the pre-existing dislocation but repulsion of another part of the dislocation. Weatherly and Nicholson have observed the glide of dislocations to the inclusion interface to relieve misfit.24 Consequently, one can find a disorganized array of dislocations in the vicinity of an inclusion with the attracted part of the dislocation lying in the interface but the repelled line length of the same dislocation lying away from the interface. The attraction of dislocations to the interface by glide will be hindered by the Peierls–Nabarro frictional stress resisting dislocation glide. When the attractive stress arising from the misfit stress is reduced to the value of the frictional stress on dislocations, then this glide process will stop and a residual strain, δr, will remain in the inclusion. The 'equilibrium' misfit δ'eq of the inclusion is now a constrained equilibrium, prevented by the frictional forces from reaching the true mechanical equilibrium and hence δ'eq > δeq.
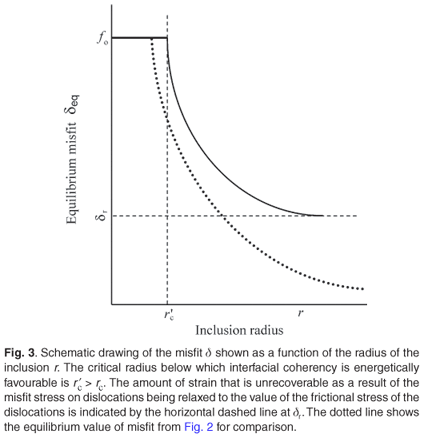
A comparison of the two values of strain is shown as a function of the size r of the inclusion in Fig. 3. The critical radius rc above which it is energetically favourable for the interface to lose coherency, i.e. when the misfit stress is equal to the line tension, is unchanged. However, the critical size at which the misfit stress on the gliding dislocation overcomes both the line tension and the frictional stress is r'c, which is greater than rc. In other words, the value of the misfit δ for which a force balance is achieved between the driving stress and the resisting forces of line tension and frictional stress is now higher than the equivalent value obtained when total energy (excluding frictional stress) is minimized. The value of d for which the force balance is achieved will be larger than that given by the minimization of energy and the asymptotic value of d will no longer be zero but a finite value δr. This situation is shown in Fig. 3, where the increased critical radius r'c is shown as well as the residual strain dr, both values being marked by dashed lines. For comparison purposes the equilibrium misfit given by energy minimization and sketched in Fig. 2 is superimposed on Fig. 3 and is denoted by a dotted line. One sees that for a given inclusion size the misfit strain is larger when frictional stress in added to the model.
Estimation of residual strain
The foregoing analytical treatment of the elastic strain present in an inclusion has been from the point of view of energy balance; however, introduction of the Peierls–Nabarro frictional stress into the model is more easily acccomplished in a model based on balancing forces on dislocations. The energy or force balance approaches are equivalent in principle but differ in detail. The critical radius rc derived from an energy balance is equivalent to a balance of forces between the misfit stress attracting a pre-existing dislocation into the inclusion interface to relieve misfit, on the one hand, and the line tension of the dislocation to increase its line length, on the other hand. This argument has been used successfully in epitaxial thin films as pioneered by Matthews.9–11 In this model the line tension of the dislocation, Ft, is given by

where d is a cut-off radius of the dislocation strain field and C is a constant proportional to b2 and a combination of elastic constants and a geometrical factor.15 The misfit driving force on the dislocation, Fε, for thin films of thickness h is given by

where D is another constant proportional to b elastic constants and another geometrical factor.15 Equilibrium is given by the force balance

Equation (12) allows one to calculate both the critical thickness for the introduction of misfit dislocations and the equilibrium elastic strain.
Modification of this approach to include the effect of friction and barriers to dislocation motion is accomplished by adding frictional forces to that of the line tension, as has been accomplished for thin films.13–18 The force balance in Equation (12) is replaced by another force balance equation, namely,

where the frictional force Ff includes the Peierls–Nabarro contribution Fp and other pinning forces such as impurity atmospheres around the dislocation axis.
In an analogous manner the inclusion may be modelled by balancing forces as in Equation (13) but now taking into account the inclusion geometry, which is different from that of the thin film. The mechanism being considered here is that of a pre-existing dislocation near the inclusion being attracted to the interface by the strain e that exists in the matrix. The maximum value of this strain occurs at the interface and is given by Equation (5). The nearby dislocation can glide into the interface only on one side of the inclusion because, from Equation (9), if it circles the inclusion, it ceases to accommodate misfit on the other side as the misfit-accommodating component of the dislocation changes sign and increases the misfit rather than relieving it. The force balance for the nearby dislocation is similar to that of nucleating a half loop in thin films15 and is taken to be sufficiently represented by the situation drawn in Fig. 4.
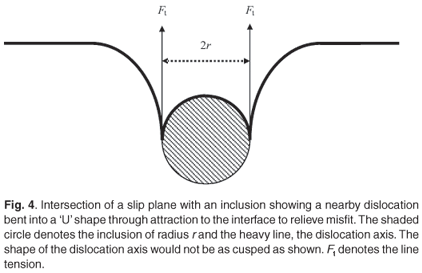
One can see that two line tension forces now resist attraction of the dislocation to the interface because the dislocation line is bent into a 'U' shape with the bottom of the U conforming to the curve of the interface and the two arms of the U forming the line tension that opposes the force of attraction to the interface. The force balance now becomes

where the expression of the line tension is taken to have the same form as in Equation (10) but with a different value of C,15,25

where the cut-off radius is approximated as half the spacing between dislocation legs, r. The misfit force attracting the nearby dislocation is now

and the frictional force is taken as the Peierls–Nabarro frictional force, Fp. This force varies with the material class but a simplified version for metals and semiconductors is

with Ui the activation energy for a particular type of dislocation, A a constant to be determined experimentally, and k and T are Boltzmann's constant and temperature, respectively.
One can use these equations to calculate the critical radius r'c by substituting Equations (15–17) into Equation (14) and solving for r. The result is
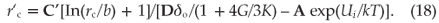
While the constants C' and D have been given in the literature,15 the values of A and Ui have to be determined by experiment. In a similar manner the constrained equilibrium value of the misfit δ'eq of the inclusion in its matrix can also be calculated from Equation (14). It is expressed here as
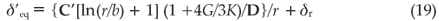
with
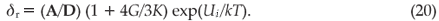
Concluding remarks
The expressions presented here contain simplifications that allow the ideas to be seen more clearly than when more detail and exactness are included in the equations. The quantitative use of the equations to evaluate a critical radius or a residual strain requires experimental measurement of the frictional stress constants A and Ui, both of which are material specific. It is important to realize that when measurements of strain are made, one should expect that true equilibrium will not be achieved but, instead, once the critical radius has been exceeded, the system will relax the elastic strain in an inclusion by generation of misfit dislocations until the driving stress has been lowered to the frictional stresses, at which point dislocation motion will cease and further strain relaxation will not occur. This results in a value of strain that may be small or not, depending on the temperature of the material during 'equilibration'. The conclusion from this is that thick films or large inclusions cannot be used as reference crystals that have bulk lattice parameters. Furthermore, even for a free material that has not been constrained by a crystal in contact with it, there are surface stresses that can be quite large. The strain induced by a curved surface of surface stress σ will be compressed by a hydrostatic pressure P,

which may be very large for small r. In the case of an inclusion, the interfacial stress may cause pressures that exceed the misfit pressure, which is

In the model developed in this paper, the strain induced by the surface stress has been ignored but to first order it can be added to that of the misfitting inclusion.26
I thank J.H. Malherbe and his colleagues in the Department of Physics of the University of Pretoria for making my sabbatical visit to their department a pleasure.
1. Mott N.F. and Nabarro F.R.N. (1940). An attempt to estimate the degree of precipitation hardening with a simple model. Proc. Phys. Soc. (Lond.) 52, 86–89. [ Links ]
2. Nabarro F.R.N. (1940). Influence of elastic strain on the shape of particles segregating in an alloy. Proc. Phys. Soc. (Lond.) 52, 90–104. [ Links ]
3. Nabarro F.R.N. (1940). Strains produced by precipitation in alloys. Proc. Roy. Soc. A 175, 519–538. [ Links ]
4. Peierls R. (1940). Proc. Phys. Soc. (Lond.) 52, 34–37. [ Links ]
5. Nabarro F. R. N. (1947). Dislocations in a simple cubic lattice. Proc. Phys. Soc. (Lond.) 59, 256–272. [ Links ]
6. Weatherly G.C. (1968). Strain field of a coherent cube-shaped particle. Phil. Mag. 17, 647–648. [ Links ]
7. Baker R.G., Brandon D.G. and Nutting J. (1959). The growth of precipitates. Phil. Mag. 4, 1339–1345. [ Links ]
8. Brown L.M., Woolhouse G.R. and Valdré U. (1968). Radiation-induced coherency loss in a copper-cobalt alloy. Phil. Mag. 17, 781–789. [ Links ]
9. Matthews J.W. (1959). Growth defects in face-centered cubic metal foils prepared by evaporation. Phil. Mag. 4, 1017–1029. [ Links ]
10. Matthews J.W. (1961). The observation of dislocations to accommodate the misfit between crystals with different lattice parameters. Phil. Mag. 6, 1847–1849. [ Links ]
11. Jesser W.A. and Matthews J.W. (1967). Evidence for pseudomorphic growth of iron on copper. Phil. Mag. 15, 1097–1106; (1968). Pseudomorphic deposits of cobalt on copper. Phil. Mag. 17, 461–473. [ Links ]
12. Jesser W.A. (1969). On the theory of loss of coherency by spherical precipitates. Phil. Mag. 19, 993–999. [ Links ]
13. Matthews J.W., Mader S. and Light T.B. (1970). Accommodation of misfit across the interface between crystals of semiconducting elements or compounds. J. Appl. Phys. 41, 3800–3804. [ Links ]
14. Dodson B.S. and Tsao J.T. (1987). Relaxation of strained-layer semiconductor structures via plastic flow. Appl. Phys. Lett. 51, 1325–1327. [ Links ]
15. Jesser W.A. and Fox B.A. (1990). On the generation of misfit dislocations. J. Elec. Mater. 19, 1289–1297. [ Links ]
16. Fox B.A. and Jesser W.A. (1990). The effect of frictional stress on the calculation of critical thickness in epitaxy. J. Appl. Phys. 68, 2801–2808. [ Links ]
17. Kui J. and Jesser W.A. (1991). Thermal relaxation in strained InGaAs/GaAs heterostructures. J. Elec. Mater. 20, 827–831. [ Links ]
18. Jesser W.A. (1992). The role of frictional stress in misfit dislocation generation. Scripta Met. Mat. 27, 675–680. [ Links ]
19. van der Merwe J.H. (1950). The stresses and energies associated with intercrystalline boundaries. Proc. Phys. Soc. (Lond.) A63, 616–637. [ Links ]
20. van der Merwe J.H. (1963). Crystal interfaces I, Semi-infinite crystals. J. Appl. Phys. 34, 117–122; Crystal interfaces II, Finite overgrowths. J. Appl. Phys. 34, 123–127. [ Links ]
21. van der Merwe J.H. and Jesser W.A. (1988). An exactly solvable model for calculating critical misfit and thickness in epitaxial superlattices: Layers of equal elastic constants and thicknesses. J. Appl. Phys. 63, 1509–1517. [ Links ]
22. Jesser W.A. and Kuhlmann-Wilsdorf D. (1967). On the theory of interfacial energy and elastic strain of epitaxial overgrowths in parallel alignment on single crystal substrates. Phys. Stat. Sol. 19, 95–105. [ Links ]
23. Kuhlmann-Wilsdorf D. (1976). Interactions between vacancies and dislocations. In Frontiers in Materials Science: Distinguished Lectures 8, eds C. Stein and L.E. Murr, pp. 253–292. New York. [ Links ]
24. Weatherly G.C. and Nicholson R.B. (1968). Electron microscope investigation of the interfacial structure of semicoherent precipitates. Phil. Mag. 17, 801–831. [ Links ]
25. Hirth J.P. (1963). Relation between Structure and Strength in Metals and Alloys, p. 218. H.M.S.O., London. [ Links ]
26. Cahn J.W. and Larche F. (1982). Surface stress and the chemical equilibrium of small crystals. II, Solid particles embedded in a solid matrix. Acta Met. 30, 51–56. [ Links ]
Received 8 August. Accepted 28 September 2008.
* Permanent address: Department of Materials Science and Engineering, University of Virginia, Charlottesville, Virginia 22904, U.S.A. E-mail: waj@cms.mail.virginia.edu














