Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.104 no.7-8 Pretoria Set./Ago. 2008
RESEARCH ARTICLES
Improvement in the modelling of geomagnetically induced currents in southern Africa
E.H. BernhardiI, III, *, ª; P.J. CilliersII; C.T. GauntIV
INational Astrophysics and Space Science Programme, Department of Mathematics and Applied Mathematics, University of Cape Town, Private Bag, Rondebosch 7701, South Africa
IIHermanus Magnetic Observatory, P.O. Box 32, Hermanus 7200, South Africa
IIICSIR National Laser Centre, P.O. Box 395, Pretoria 0001, South Africa
IVDepartment of Electrical Engineering, University of Cape Town
ABSTRACT
One of the consequences of the geomagnetic storms resulting from adverse space weather is the induction of geomagnetically induced currents (GICs) in power lines. The GICs that flow in a power transmission network are driven by the induced electric field at the Earth's surface. The electric field, in turn, is affected by the changing magnetic field during a magnetic storm. These GICs can cause extensive and expensive damage to transformers in the power transmission system. Understanding the behaviour of the magnetic field during a magnetic storm is a crucial step in modelling and predicting the electric field and ultimately the GICs in a power transmission network. We present a brief overview of the present status of GIC modelling in southern Africa and then discuss whether it is sufficient to use geomagnetic data from a single magnetic observatory alone to model GICs over the subcontinent. A geomagnetic interpolation method is proposed to improve the modelling of GICs in southern Africa. This improved model is one step closer to our being able to predict GICs accurately in the subcontinent, which will enable power distribution companies to take the necessary precautions to minimize possible transformer damage.
Introduction
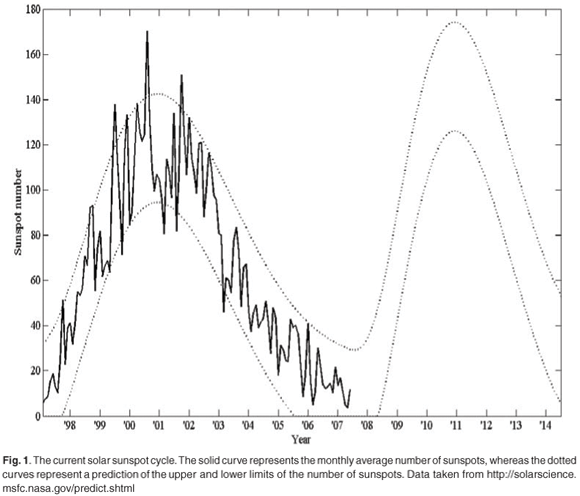
One of the consequences of geomagnetic storms that result from adverse space weather is the induction of geomagnetically induced currents (GICs) in power lines. The frequency of adverse space weather is closely linked to the incidence of coronal mass ejections (CMEs) from active areas on the surface of the Sun, known as sunspots, particularly during sunspot-cycle maxima. On the other hand, during sunspot-cycle minima, co-rotating interaction regions (CIRs) are mostly responsible for magnetic storms. Solar activity, as measured by the sunspot number, seems to follow an 11-year sunspot cycle. Figure 1 represents the current sunspot cycle, Cycle 23. Cycle 24 began in January 2008. During a period of maximum sunspot number, the solar activity is statistically at a maximum, and vice versa. The next solar maximum (during sunspot Cycle 24) is predicted to occur around 2011. CMEs also arise at times other than at solar maximum, however, like the well-known Halloween storm of October 2003, which occurred in the waning phase of sunspot Cycle 23. GICs are the last step in a chain of events that start with CMEs on the Sun. This chain of events can be summarized as follows:
• Coronal mass ejection
The Sun continuously emits energetic particles (ions) in the form of plasma into interplanetary space. This plasma, travelling through the heliosphere, is called the solar wind, and typically consists of hydrogen and helium ions and electrons, and drags some magnetic flux out of the Sun to fill the heliosphere with a weak interplanetary magnetic field (IMF). When a CME occurs, it results in the ejection of enormous additional amounts of high-energy ions (plasma) into interplanetary space. A CME directed at the Earth can cause a sudden increase in the solar wind pressure from 2 nPa to as much as 30 nPa, an increase in the solar wind velocity from an average of 400 km/s to as much as 2000 km/s, as well as a rapid change in the interplanetary magnetic field from typically 5 nT to 30 nT. The solar wind velocity was close to 2000 km/s during the storm of October 2003.1 These sudden changes, in turn, disturb the Earth's magnetosphere and can initiate geomagnetic storms. It is now well established that CMEs are the drivers of practically all large geomagnetic storms, with Dst values** less than –100 nT. The southward component of the typically-rapid magnetic field fluctuations within CIRs, on the other hand, through sporadic magnetic reconnection with the Earth's geomagnetic field, lead to weak to moderate intensity magnetic storm main phases with Dst values greater than –100 nT.
• Interaction between the solar wind and the Earth's magnetosphere
The Earth's magnetosphere extends to about ten Earth radii towards the Sun. The solar wind propagates towards Earth, where it interacts with the magnetosphere through a process called reconnection. Reconnection of the Earth's day-side magnetic field with the IMF readily facilitates the transfer of momentum and energy from the solar wind into the Earth's magnetosphere. The direction and magnitude of the IMF determines the efficiency of the interaction with the magnetosphere. If the IMF is directed southward, that is, opposite to the Earth's magnetic field, the resulting disturbance of the Earth's geomagnetic field can be quite large.2
• Interaction between the magnetosphere, ionosphere and the Earth's surface
The ionosphere is the ionized layer of the upper atmosphere, extending from 100 km to about 1000 km above the Earth. The coupling between the magnetosphere and the ionosphere is a complex plasma process that gives rise to increases and rapid variations (on a time-scale of 1–1000 s) in the geomagnetic field at the Earth's surface.3 This is known as a geomagnetic storm, during which an electric field at the Earth's surface is induced according to Faraday's law of induction:

with E as the induced electric field at the Earth's surface in V/m and B the magnetic field in tesla. ∂B/∂t is the rate of change in the geomagnetic field and ∇ × E indicates the curl operator acting on E. The electric field that is induced at the Earth's surface causes different areas on the ground to be at different electric potentials. When we consider two different grounding points of the power transmission system at different locations, typically at electrical substations, a current will flow from the point of higher electric potential to one of lower potential. The currents that flow to the ground via the power transformers are known as GICs. These currents are induced not only in conductors like power transmission lines, but also in telecommunication cables and conducting pipes on or below the Earth's surface.
The typical frequency range of GICs is 1–0.001 Hz (period 1–1000 s).4 This frequency is much less than the alternating current of 50 Hz (period 0.02 s) at which the South African power transmission system operates. These quasi-d.c. GICs cause half-cycle saturation in the magnetic circuits of the transformers and can be responsible for extensive damage to transformers in the transmission network. This leads to power outages and may require expensive replacement of defective transformers. Even though magnetic field changes, caused by solar storms, are more severe at greater latitudes,3 the long transmission lines in southern Africa allow for the induction of relatively high GICs, and there is substantial evidence that several power transformer failures in the subcontinent have been caused by extreme geomagnetic activity.5,6
We provide a brief overview of the method presently used to model the GICs at a power transmission substation by using measured geomagnetic data. We then consider a case to show that it is insufficient to use geomagnetic data from a single magnetic observatory alone to model GICs in our region, as has been done previously.7 We then describe a geomagnetic interpolation method to improve the existing model to calculate GICs in southern Africa.
Present status of GIC modelling in southern Africa
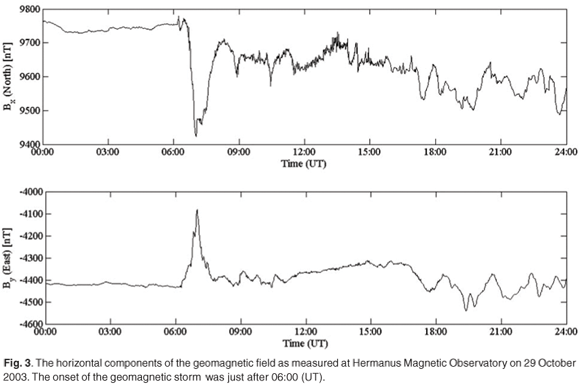
The GIC modelling process can be divided into two steps.8 First, the surface electric field must be determined from the changing geomagnetic field using Faraday's law of induction [Equation (1)]. Once the electric field is known, the GIC in the power transmission system can be calculated from the configuration of the power lines and the ground resistance. This modelling process is demonstrated with data from a severe geomagnetic storm that took place on 29 October 2003, the so-called Halloweenstorm, which resulted in extensive damage to power transformers in this region (Fig. 2).

• Geomagnetic field to electric field
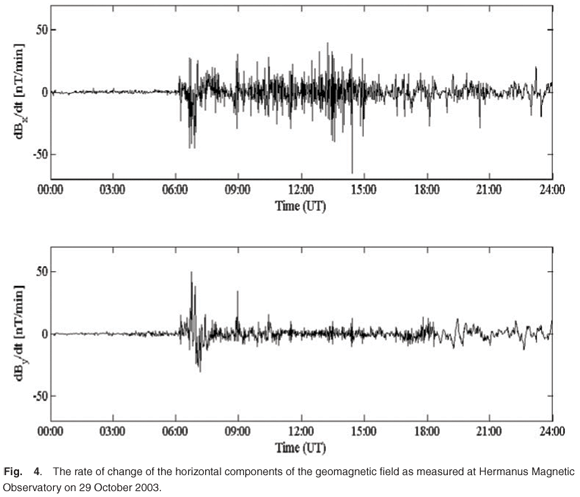
Consider the horizontal components Bx and By of the geomagnetic field as measured at the Hermanus Magnetic Observatory (HMO) on 29 October 2003 (Fig. 3). The Bx component is directed north and the By component directed east. The first rapid change in Bx and By is associated with the start of the geomagnetic storm at 06:00 (UT). The rate of change of the horizontal components of the geomagnetic field, as shown in Fig. 4, is the driver of the GICs. The electric field can be determined from the magnetic field by9
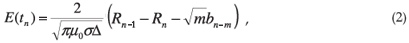
where µ0 is the permeability of free space, σ is the conductivity of the Earth (taken as 0.001 S m–1), Δ is the sampling interval, n is the sample number and

where bn = Bn – Bn–1 denotes the change in Bx (or By) between observations at time tn and the preceding observations at time tn–1. Note that the electric field is not only determined by the current value of the geomagnetic field, but is also affected by past values of the geomagnetic field. This is why the index m is introduced in Equations (2) and (3). The value of m determines how far back in time that contributions from the geomagnetic field are still considered. By applying Equations (2) and (3), with m taken to be 10, the electric field can now be calculated7 (Fig. 5). The value m = 10 was used, as it was employed in previous work to model GICs in southern Africa7 accurately. A further investigation is needed in order to determine whether m = 10 is indeed the optimum value of m
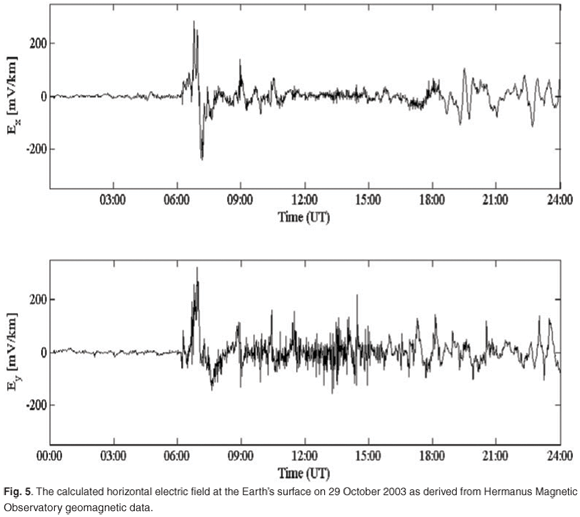
• Electric field to GICs
The next step is to determine the GICs from the induced electric field at the Earth's surface. The electric field at the location of each transformer can be calculated by using Equation (2). If it is assumed that the electric field is spatially constant over the region where the GICs are calculated, then the current can be determined from8,9

where a and b are coefficients that depend on the topology and geometry of the power transmission network. These coefficients vary as the network configuration changes with location and time. The GIC is determined for the Eskom Grassridge substation near Port Elizabeth for the purposes of the calculation presented here. The values for a and b at Grassridge are taken to be –80 and 15, respectively.7 Figure 6 illustrates the modelled GIC at Grassridge during the geomagnetic storm. The plus or minus sign indicates the polarity of the current. This method of calculating GICs in this region has been implemented by Koen.7
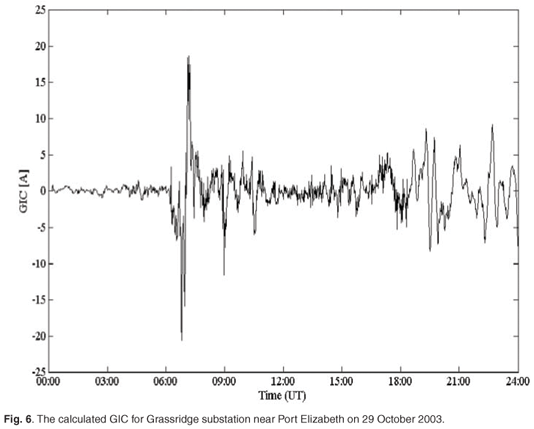
Challenges for the modelling of GICs in southern Africa
Geomagnetic data from only one observatory, at Hermanus, were used7 in previous attempts at modelling the GICs in the subcontinent. GICs in Finland could not be modelled accurately at a particular site by using geomagnetic data from a magnetic observatory more than about 300 km away from that location.8 Because a particular GIC site in southern Africa can be several hundred kilometres away from Hermanus, where the geomagnetic measurements are taken, could be one of the reasons why there have been differences between previous models and measured GICs in the region.5
The sparsity of geomagnetic observatories is another major disadvantage in modelling GICs in the subcontinent. At the time of this research, there were three functional geomagnetic observatories in southern Africa, namely at Hermanus (HER) and Hartebeesthoek (HBK) in South Africa, and Tsumeb (TSU) in Namibia.
Another difficulty is obtaining the most recent information regarding the configuration of the power transmission network, in order to determine accurate values for the network coefficients a and b in Equation (4).
Improvements in the modelling of GICs in southern Africa
To show that the location, where the geomagnetic data are taken, is of importance in modelling GICs, see Fig. 7 for a comparison of GIC results at the Hydra substation (De Aar), as calculated with Hermanus and Hartebeesthoek geomagnetic data, respectively, and assuming a constant network configuration for all the cases. (The five storms that were investigated had the highest Kp-index (a classification of the severity of the magnetic storm that ranges between 0 and 9, with 9 being the most severe) for that particular year.) As can be seen from the figure, for the Hydra substation, which is nearer to Hartebeesthoek than to Hermanus, the GICs according to HBK data are always more severe than those according to HMO data. Table 1 gives the difference in maximum GIC at Hydra according to HMO and HBK magnetic data, respectively. For Hydra, the GIC has on average been underestimated by 21% when HMO data are used instead of HBK data. For the Matimba substation near Lephalale, HBK delivers GICs that have on average been 16% higher than those calculated with HMO data. The GIC at the Beta substation has been underestimated by 20% when HMO magnetic data are used instead of HBK data. Further investigation is needed for the other substations in southern Africa, but based on the data from the three substations mentioned above, it seems necessary to acquire geomagnetic data that are closer to the GIC site of interest, in order to improve GIC modelling and, ultimately, GIC forecasting in the subcontinent.
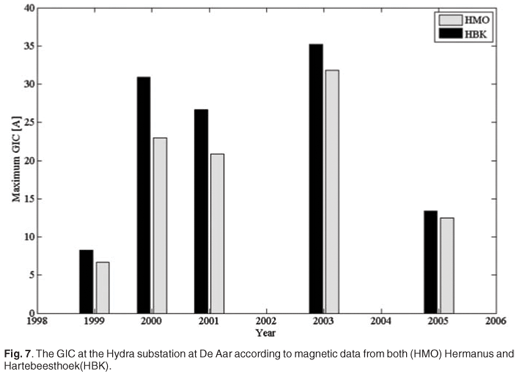

Interpolating the geomagnetic field
It should be possible to obtain a more accurate value for the variation of the geomagnetic field at the GIC site of interest by using some form of interpolation between the sites where the magnetic field is observed. The interpolation method proposed in this paper is the spherical elementary current system (SECS) based on equivalent elementary currents in the ionosphere.10,11 This method is an inversion technique, where observed geomagnetic data are used to infer equivalent ionospheric currents. SECS would typically be used in highly disturbed geomagnetic events where the ionospheric contribution to the geomagnetic variation is more than 80%.12 It is not possible to construct the true 3-D ionospheric current system from ground-based geomagnetic measurements alone. For every 3-D magnetic field variation, there exists a horizontal equivalent current system that reproduces the same geomagnetic field at the surface of the Earth.13 It is important to note that these equivalent ionospheric currents are not real currents, but hypothetical constructs that reproduce the observed geomagnetic field at the Earth's surface. Planar geometry is used for this application, instead of spherical geometry, as GICs are a regional phenomenon for which the curvature of the Earth can be neglected as a first approximation. The surface current density vector of such an elementary equivalent ionospheric current system at height h, with amplitude I, in cylindrical coordinates is8,14

where 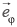 is the unit vector in the φ-direction,
is the unit vector in the φ-direction, 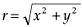 and the x–y plane is the Earth's surface. The horizontal geomagnetic field vector due to such an elementary current system is8
and the x–y plane is the Earth's surface. The horizontal geomagnetic field vector due to such an elementary current system is8

where 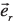 is the unit vector in the radial direction, µ0 is the permeability of free space, h is the height of the ionospheric current element above the Earth's surface, r is the radial distance from the current element to the field point, and I is the amplitude of the equivalent current. The equivalent ionospheric current elements are placed in an equally-spaced grid (a 15 × 15 grid was used in this model, which translates to a grid spacing of ~115 km) at a height of 100 km above the subcontinent. The amplitudes of these current elements can be calculated by fitting the modelled horizontal geomagnetic field (due to ionospheric elementary currents) to the measured horizontal geomagnetic field as exists8 at the geomagnetic observatories at Hermanus, Hartebeesthoek and Tsumeb:4
is the unit vector in the radial direction, µ0 is the permeability of free space, h is the height of the ionospheric current element above the Earth's surface, r is the radial distance from the current element to the field point, and I is the amplitude of the equivalent current. The equivalent ionospheric current elements are placed in an equally-spaced grid (a 15 × 15 grid was used in this model, which translates to a grid spacing of ~115 km) at a height of 100 km above the subcontinent. The amplitudes of these current elements can be calculated by fitting the modelled horizontal geomagnetic field (due to ionospheric elementary currents) to the measured horizontal geomagnetic field as exists8 at the geomagnetic observatories at Hermanus, Hartebeesthoek and Tsumeb:4
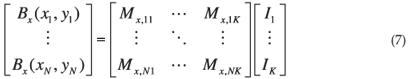
The left-hand side of this linear matrix equation is the x-directed component of the geomagnetic field, as measured at the different magnetic observatories. On the right-hand side of Equation (7) is the component of the modelled geomagnetic field4
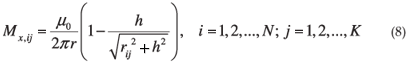
at the point (xi, yi), i = 1, 2,..., N on the Earth's surface due to a current element of unit amplitude at (xj, yj), j = 1, 2,..., K and height 100 km above the Earth. Here, rij denotes the radial distance between the source and field points. The linear system represented by Equation (8) is usually underdetermined, due to the number of measurements being much less than the number of required elementary currents (K > N), and must be solved by means of singular value decomposition (SVD).4 The above calculation is performed for Bx. A similar linear system can be constructed for By. The solution of this linear system gives the equivalent ionospheric current amplitudes that reproduce the geomagnetic fields measured at the magnetic observatories. From these equivalent currents, it is now possible to determine the horizontal geomagnetic field at any point (x, y). This method delivers an interpolation technique for the geomagnetic field,8 which makes it possible to determine the geomagnetic field close to the site of interest for GIC calculation. This in turn allows a corresponding interpolation of the electric field over the entire region of interest (Fig. 8).
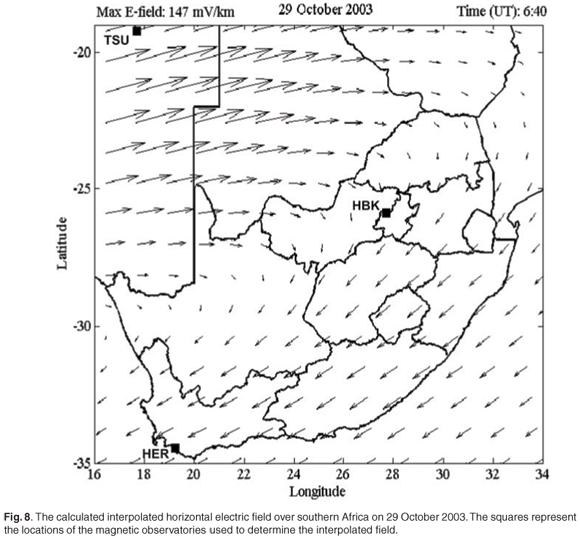
At first glance, using this interpolation method might appear as a contradiction, since Equation (4) assumes a plane-wave disturbance of the geomagnetic field, and by using SECS, it shows that the geomagnetic field disturbance is indeed variable (plane wave) over the entire region of interest. The greatest contribution to the GICs at a site of interest is from the geomagnetic disturbance (and thus the induced electric field) close to the site. This plane-wave method [Equation (4)] can be very accurate,8 if we isolate the particular GIC site and assume that the value of the geomagnetic field over the entire region is a plane wave, with the value of the interpolated geomagnetic field at the GIC site.
Figure 9 illustrates the difference between using data from a single observatory versus the SECS interpolation method to calculate GICs. As a measure of effectiveness, we first considered the maximum measured GIC of 12.55 A at the Grassridge substation, which was recorded at 06:48 (UT) on 29 October 2003, and we compared how well this value could be modelled. By using only the geomagnetic field at Tsumeb, which is the observatory farthest from Grassridge, to calculate the GIC, the error in the modelled value of the maximum GIC was 81%. But by using the SECS interpolation method and the measured geomagnetic field from all three observatories (HER, HBK and TSU), the modelling error could be reduced to 12%. As an alternative measure of effectiveness over the duration of the storm, we considered the variance of the modelling error as a percentage of the root mean squared value of the GIC, which was reduced from 59% in the case of using only Tsumeb data in the model, to 25% when the SECS interpolation was used.
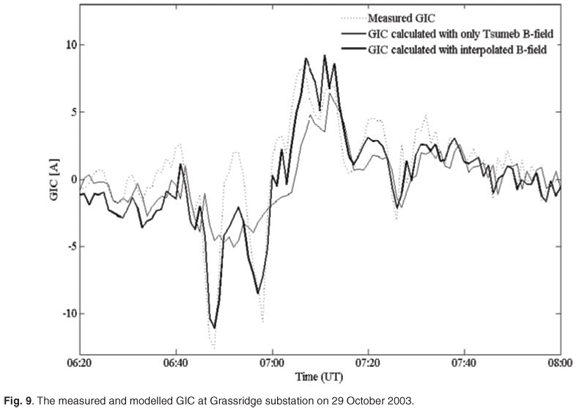
The SECS interpolation method, in conjunction with the plane wave GIC model, has been used with great success in Finland to model GICs, even with a relatively sparse magnetometer network.8
Conclusion and proposals for future work
GICs arise in southern Africa's power transmission system, and large currents induced during geomagnetic storms can cost Eskom, the national electrical utility, millions of rands as a result of transformers that are damaged, either latently or radically. By using data from only one magnetic observatory, GICs cannot be modelled as accurately as when data from other magnetic observatories in the region are included.
Since the geomagnetic data used for modelling and predicting GICs should be determined at the site of interest, we have implemented an interpolation method to model the geomagnetic field at desired locations. The SECS delivers a powerful method for interpolation of the geomagnetic field, in order to produce geomagnetic data close to the sites of interest. The interpolated magnetic data can then be used to model GICs in the subcontinent more accurately than by previous methods.
It is crucial to have more magnetic observatories in southern Africa for the SECS interpolation method to achieve its full potential. Currently, the SECS method is very useful for post-event analysis, but if we can forecast the geomagnetic field at observation stations using patterns in our observations from these stations, then the interpolated geomagnetic field data will be available to predict GICs anywhere in the subcontinental power transmission network. Future work will include refining the SECS interpolation method by using a more realistic ground resistivity model for the region. The current assumptions of planar geometry might be extended to accommodate spherical geometry.
A possible way of forecasting the geomagnetic field, and ultimately GICs, is to implement a type of artificial intelligence computer algorithm, known as a neural network, to predict the geomagnetic field from an analysis of past records of the geomagnetic field at a particular magnetic observatory. This could be done by investing the program with as much historical data as is possible, giving the location of the observatory, the solar wind velocity, solar wind density, and IMF field values, with the corresponding outcomes. The program should then learn to recognize trends, which would allow it to predict an outcome on presentation of a new input data set. This could make it possible to predict GICs up to one hour in advance, depending on the availability of solar wind data from the ACE, SOHO or other satellites that continuously monitor the solar wind parameters. These satellites are located at a point between the Earth and the Sun where the nett gravitational force is zero, as the Earth's and the Sun's gravitational fields essentially cancel each other. This position is referred to as the Lagrangian point 1. It typically takes the solar wind one hour to reach the Earth from this point. Such a real-time GIC forecasting system in southern Africa will allow power distribution companies such as Eskom (in South Africa) and NamPower (in Namibia) to take pre-emptive measures in order to protect the equipment that is at risk.
This research contributes a key step towards improving the forecasting of GICs in southern Africa, through the advantage that the SECS interpolation method interpolates the geomagnetic field as accurately as is currently possible with the existing configuration of magnetic observatories in the region.
We thank Patrick Sibanda, Elijah Oyeyemi and Pieter Kotze of the Hermanus Magnetic Observatory for their advice and comments on the paper. We would also like to thank Eskom and EPRI's Sunburst project for providing us with measured GIC data, in order to validate our model.
1. Skoug R.M., Gosling J.T., Steinberg J.T., McComas D.J., Smith C.W., Ness N.F., Hu Q. and Burlaga L.F. (2004). Extremely high speed solar wind: 29–30 October 2003. J. Geophys. Res. 109, A09102 [ Links ]
2. Pirjola R. (2002). Geomagnetic effects on ground-based technological systems. Surv. Geophys. 23, 71–90. Pirjola R., Kauristie K., Lappalainen H., Viljanen A. and Pulkkinen A. (2005). Space weather risk. Space Weather 3, S02A02. [ Links ]
3. Pulkkinen A. (2003). Geomagnetic induction during highly disturbed space weather conditions: Studies of ground effect. Ph.D thesis, University of Helsinki, Finland. [ Links ]
4. Koen J. and Gaunt C.T. (2002). Geomagnetically induced currents at mid-latitudes. In Proc. International Union of Radio Science (URSI) General Assembly, Maastricht. [ Links ]
5. Gaunt C.T. and Coetzee G. (2007). Transformer failures in regions incorrectly considered to have low GIC-risk. In Proc. IEEE Powertech Conference, July, Lausanne. [ Links ]
6. Koen J. (2002). Geomagnetically induced currents in the Southern African electricity transmission network. Ph.D. thesis, University of Cape Town, South Africa. [ Links ]
7. Viljanen A., Pulkkinen A., Amm O., Pirjola R., Korja T. and BEAR working group (2004). Fast computation of the geoelectric field using the method of elementary current systems and planar Earth models. Annal. Geophys. 22, 101–113. [ Links ]
8. Viljanen A. and Pirjola R. (1989). Statistics on geomagnetically-induced currents in the Finnish 400 kV power system based on recordings of geomagnetic variations. J. Geomagn. Geoelec. 41, 411–420. [ Links ]
9. Amm O. and Viljanen A. (1999). Ionospheric disturbance magnetic field continuation from the ground to the ionosphere using spherical elementary current systems. Earth Planets Space 51, 431–440. [ Links ]
10. Pulkkinen A., Amm O., Viljanen A. and BEAR working group (2003). Separation of the geomagnetic variation field on the ground into external and internal parts using the spherical elementary current system method. Earth Planets Space 55, 117–129. [ Links ]
11. Tanskanen E.I., Viljanen A., Pulkkinen T.I., Pirjola R., Häkkinen L., Pulkkinen A. and Amm O. (2001). At substorm onset, 40% of AL comes from underground. J. Geophys. Res. 106, 13119–13134. [ Links ]
12. Pirjola R. and Viljanen A. (1998). Complex image method for calculating electric and magnetic fields produced by an auroral elecrojet of a finite length. Annal. Geophys. 16, 1434–1444. [ Links ]
13. Amm O. (1997). Ionospheric elementary current systems in spherical coordinates and their application. J. Geomag. Geoelec. 49, 947–955. [ Links ]
Received 7 April. Accepted 14 June 2008.
* Author for correspondence. E-mail: e.h.bernhardi@ewi.utwente.nl
** The Dst (disturbance storm time) index is an hourly average of the low-latitude horizontal magnetic variation. This gives an estimate of the global depression of the horizontal magnetic field that is caused by the westward flowing high-altitude equatorial ring current during large magnetic storms.
a Present address: Integrated Optical MicroSystems, MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, Enschede, 7500 AE, the Netherlands














