Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.7-8 Pretoria Sep./Aug. 2008
RESEARCH ARTICLES
The spinning pipe gas lens revisited
C. MafusireI, II; A. ForbesI, II, *; G. SneddenIII; M.M. MichaelisII
ICSIR National Laser Centre, P.O. Box 395, Pretoria 0001, South Africa
IISchool of Physics, University of Kwazulu-Natal, Private Bag X54001, Durban 4000, South Africa
IIICSIR Defence Peace Safety and Security, P.O. Box 395, Pretoria 0001, South Africa
ABSTRACT
The graded index (GRIN-like) medium generated by gas inside a heated steel pipe when rotated about its longitudinal axis has the ability to focus a laser beam. While the effective focal length of such a system has previously been studied, there is little information on optical phase aberrations and no study to date on the propagation parameters of the laser beam, but has rather remained rooted in the domain of ray optics. We revisit the spinning pipe gas lens in this paper with new perspectives on the propagation of optical waves, and show how the position of the focus is not a measure of the focal length of the lens. We make use of both the intensity and phase information carried by waves to accurately measure the salient parameters of the lens, and complement our experimental findings with a computational fluid dynamics model.
Introduction
The device discussed in this paper is a horizontal heated steel pipe, rotated (spun) about its horizontal axis, forming a radially-graded refractive index profile in the gas within this pipe. The profile allows for wave guiding under certain conditions, and with a judicious choice of pipe length, an output beam that converges in space can be obtained. When this happens, the system is deemed to act as a lens, and is referred to as a spinning pipe gas lens (SPGL). Interest in this type of gas lens began in the early 1960s, when scientists at Bell Laboratories developed gas lenses for use as waveguides.1–5 More recently, gas lenses have been proposed as the final optical device in laser fusion and laser propulsion systems, where high average flux would otherwise cause expensive damage to solid-state lenses.6 The early gas lenses did not guide beams by being spun, but rather by a laminar flow of gas that was injected axially into a heated, stationary pipe and exhausted radially.2–5,7,8 The concept of rotating a heated metal pipe was introduced in 1975 by Martynenko,9 who showed both theoretically and experimentally that the lens overcame the asymmetric nature of the temperature field and it removed aberrations caused by free convection.
However, most of the studies carried out at that time, and since, have concentrated on the lensing aspect alone, for example, to focus intense laser beams for the drilling of holes in metal sheets, and as telescope objectives.10–14 These studies disregarded the effect the SPGL had on the wavefront of the propagating laser beam.
This paper considers the use of a Shack–Hartmann wavefront sensor to measure defocus on the optical wavefront. This sensor was developed by the US military as part of their adaptive optics programme. Laser light, traversing thousands of pinholes, is simultaneously sampled to yield phase shift data across the beam. The next section discusses some established theories of the SPGL as a waveguide. A calculation of focal length dependence on beam waist location based on an ABCD formulation is covered in the following section. A computational fluid dynamics model is subsequently presented to complement these findings, followed by the presentation of experimental results from a Shack–Hartmann wavefront sensor.
Spinning pipe gas lens
In the case of an SPGL with a density gradient which is sufficiently large, a beam propagating along the axis can be converged several times per unit distance, waveguiding it along the length. By making a judicious choice of wall temperature and pipe rotation speed, a beam will be in focus on exit, like a lens. Previous studies have shown that the SPGL imitates a graded index (GRIN) medium, with a refractive index which is maximized along the axis, and decreases parabolically with radial distance towards the walls:11,13,15,16

where r is the radial distance from the axis, γ is a radial refractive index parameter, which is a measure of the power of the SPGL, and n0 is the refractive index along the axis. The parameter γ implies that the SPGL focuses a beam g times per unit distance. This means it is possible to get either a diverging, collimating or converging laser beam after passing it through an SPGL. To obtain a converging or focused beam, the GRIN medium inside must be in the process of focusing the beam on exit, as would be the case if the SPGL terminated at point X, as shown in Fig. 1.
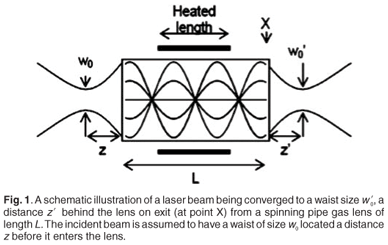
We started by repeating previous experiments16 with variation of the SPGL's beam waist location (the point where the beam size is a minimum) with changing pipe rotational speed at selected temperatures. The results are given in Fig. 2. The measurements were made by recording the intensity of the light after the SPGL. The data clearly indicate an inverse relationship between the pipe rotational speed and the resulting waist location. An empirical formula for the waist position, z', behind the lens was derived as:
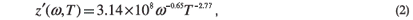
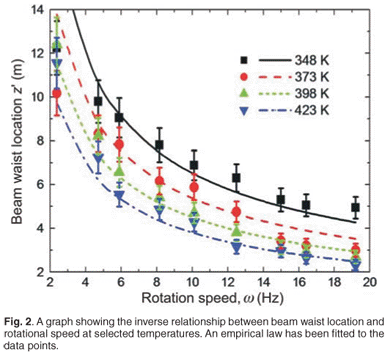
where T represents the SPGL wall temperature in kelvin and w is the pipe rotational speed – the number of revolutions of the pipe per second – and is measured in hertz. The graph also shows that with increasing temperature, the beam waist moves closer to the gas lens for a given rotational speed. The same trend is noted when increasing the rotational speed at constant temperature. If the input field to the lens is large, with a small divergence, then the effective focal length of the lens will be given approximately by the new waist distance according to Equation (2). This has been the assumption in all prior work on SPGLs. But this is not generally the case, and in the next section we derive an equation for the relationship between the focal length of the lens and the waist location z .
Laser beam propagation
The relationship between the effective focal length of the SPGL and the new waist location of the beam after the lens can be found by applying the ABCD matrix representation17 of the system. Assuming a parabolic refractive index profile, a gas lens has the matrix:
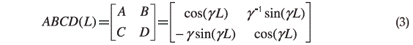
for an SPGL of length L. For a laser beam of Rayleigh range z0, whose waist, of size w0, is a distance z in front of the SPGL, the corresponding output waist position and Rayleigh range, z' and 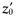 , respectively, can be acquired from:17
, respectively, can be acquired from:17

The waist of the output laser beam, of size 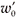 , is located at a distance z' and has a Rayleigh range given by
, is located at a distance z' and has a Rayleigh range given by 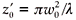 for a vacuum wavelength of λ.
for a vacuum wavelength of λ.
In this model, z' is positive or negative depending on whether the output waist is in front of or behind the SPGL, respectively. The Rayleigh range can be defined as how well a beam has been collimated; the larger it is, the more collimated is the laser beam. Equating the real parts on both sides of Equation (4), we have the relationship:
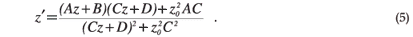
For any focusing ABCD system, the effective focal length is given by17

By combining Equations (3)–(6), we derive the following expression for the focal length of the lens in terms of the input and output beam waist positions:
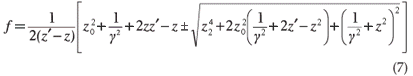
This is a significant result, as it exposes the deficiency in the past approach by many authors in assuming that the waist location after the lens is equivalent to the focal length of the lens. It also expresses the focal length in terms of measurable quantities, thus allowing an indirect route to determination of the focal length. This indirect route involves careful measurement of the beam intensity change during propagation after the SPGL in order to determine the new waist location. The intensity is measured and the beam size extracted at each propagation distance after the SPGL. One can determine the waist size and waist location by plotting the change in beam size with propagation distance. This approach, while very accurate, can be tedious as it requires the measurement of the beam size at numerous positions after the lens.
A more direct route is through measurement of the wavefront, or phase, of the laser beam. Lenses introduce a quadratic phase change across the wavefront of the light, the magnitude of which increases with lens strength in a well-known relationship.15,18 This wavefront curvature is termed as defocus, and is quantitatively described by the Z20 Zernike polynomial with weighting coefficient A20. Other higher-order terms also exist,19 which give rise to optical aberrations, having a deleterious affect on the propagation of the focused laser beam.
Computational fluid dynamic model
Computational fluid dynamics (CFD) simulation of a simplified test system was executed using the commercial CFD code, STAR–CD. Assumptions included the removal of the mounts and other three-dimensional geometry features that would complicate the geometric model. The tube, however, is accurately reproduced with the further assumption that the mounts act as a heat sink and thus the tube ends are unheated. A fully transient solution is presented in which the tube is spun up from a heated steady-state buoyancy-driven solution, and held at fixed speed until a steady state has been reached.
As indicated by Figs 3 and 4, rotation of the pipe initiates a weak longitudinal flow structure by discharging air out of the end of the pipe, close to the wall, air replacement occurring at the centre. This longitudinal flow structure is an order of magnitude weaker than the rotational flow structure (depicted in an exaggerated form in Fig. 4). It develops, with longitudinal decay of this effect, towards the middle of the pipe, where a mirror-image structure from the opposite end meets it. The development of the flow structure and its influence on the focusing function can be controlled to a limited extent by the choice of pertinent parameters such as the diameter and length of the section of unheated pipe, as it is a function of boundary layer development and pipe flow theory, albeit in a complex three-dimensional flow-field, dominated by the out-of-plane rotational effect. Turbulence is modelled using the k–ε model,20 which involves numerical solution of two coupled equations, a turbulent kinetic energy (k) equation and an energy dissipation rate (ε) equation.
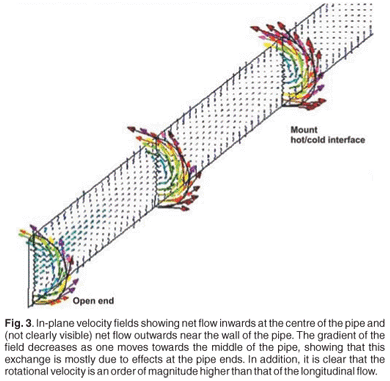
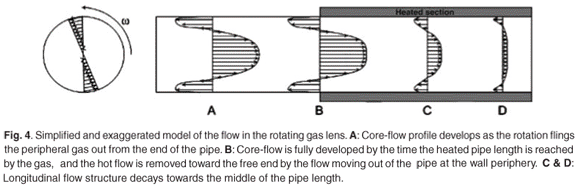
Figure 5 indicates the focusing effect caused by the interaction of the longitudinal flow structure with the thermal boundary layer of the heated pipe length. Hot gas is expelled at the outer boundaries, and cold environmental flow replaces it via the rotational axis or core of the pipe. The full thermal effect is localized to a few pipe diameters up- and downstream of the hot/cold interface at the bearing block. The initial density gradient is determined by the highly unstable interaction of buoyancy and gravitational forces, as the pipe interacts with the environment in a free convection mode. Small changes in the angle of the pipe will result in vastly different density gradients and patterns.
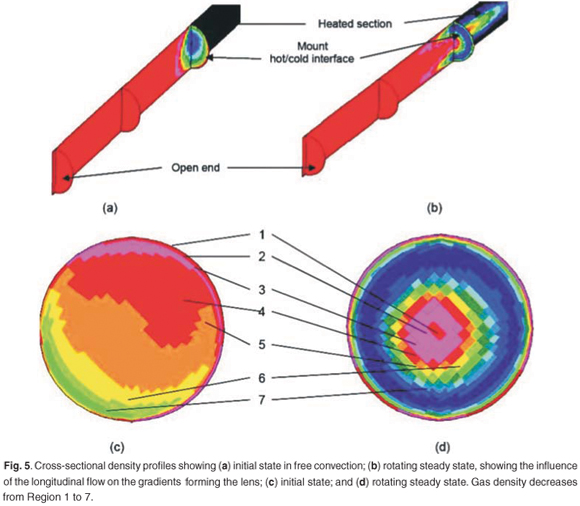
Examining the transient results, as the pipe settles into a near steady-state flow pattern, there is clear evidence of unsteadiness in the density pattern across the bearing block interface. This unsteadiness is caused by the relatively large rotational viscous forces created by the rotation of the pipe in relation to weak longitudinal flow. This results in a slow oscillation of the cold (denser) core around the pipe centre, rather than a perfectly symmetrical situation with the core perfectly stationary in the centre. Viewing from a strictly fluid dynamic point, it is clear that the longitudinal flow is the weakest of all the forces in the model, and yet it is this that drives the focusing function of the lens.
This gas dynamic behaviour provides an understanding of why the SPGL becomes a stronger lens, not only with a higher wall temperature, but also with a higher pipe rotational speed. As this speed increases, air is centrifuged and driven more quickly from the ends, and is also entrained further down the tube. The 'effective length' of the gas lens, namely the length over which there is an appreciable thermal gradient, increases. The gas dynamic model also explains why the SPGL, like conventional drawn-air lenses, suffers from aberrations. The approximately parabolic refractive index profile is the result of integration along the optical path length through a variety of non-parabolic sections, some more strongly differentiated than others. The Shack–Hartmann wavefront sensor allows one to measure the extent to which the SPGL differs from a perfect gas lens by providing inter alia a measure of all the known primary aberrations, such as tilt, defocus, coma and spherical aberration.
Wavefront measurement and results
Experimental setup
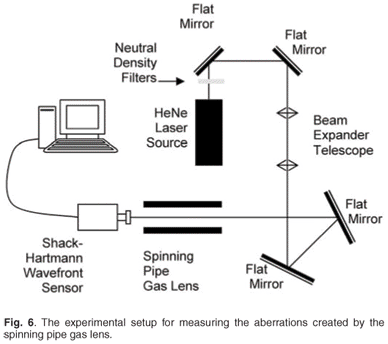
A stainless steel pipe of length L = 143 cm, with an internal diameter of 3.66 cm, was used. Ambient air was the gas phase. A heater tape was wound along a 93-cm middle section of the pipe, with bearing blocks on either side, separating the heated section from a 25-cm unheated section at each pipe end. A HeNe laser beam, expanded to about 6 mm in diameter, was directed through the gas lens. The waist position was located by observation of the distance at which the beam diameter was a minimum, inserting a removable mirror in the beam path after the lens. Without the removable mirror, the laser beam passed through the SPGL and onto the Shack–Hartmann sensor, from which frames were transferred to a computer for processing. The sensor was placed about 10 cm from the gas lens exit in order to obtain an accurate determination of the wavefront after the lens (optical wavefronts change during propagation, so free-space propagation was minimized). Suitable neutral density filters were used to avoid saturation of the wavefront sensor.
A non-rotating and unheated pipe was used as a reference device. The test pipe was heated successively to wall temperatures of 348 K, 373 K, 398 K and 423 K. At least 15 sets of wavefront measurements were acquired at each of the four temperatures and selected rotational speeds. These were averaged and the reference data subtracted to obtain a contribution from the SPGL alone. The experimental setup is shown in Fig. 6.
Results
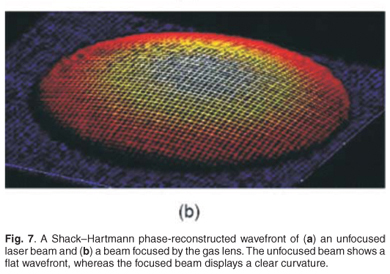
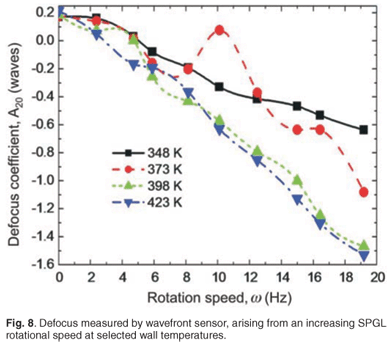
We refer to the direct measurement of the beam waist by observation of the intensity of the beam as the intensity method, whereas the indirect calculation of the new waist position by using the Shack–Hartmann wavefront sensor is termed the phase method. The raw wavefront data are shown in Figs 7(a) and (b), where the near-flat wavefront is observed when there is no lensing action. When the SPGL is active, the wavefront takes on a well-defined curvature associated with the defocus aberration. The magnitude of this defocus increases monotonically with both pipe-wall temperature and pipe rotational speed, as shown in Fig. 8.
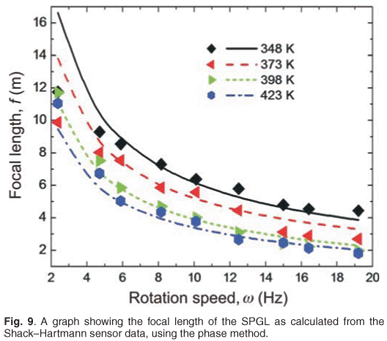
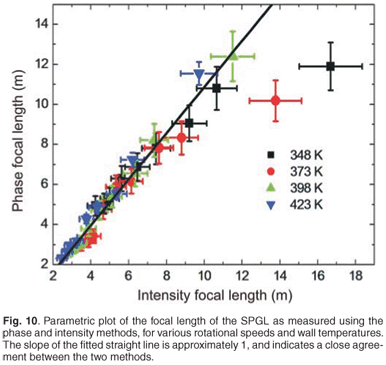
The new waist location after the SPGL was determined from a wavefront measurement, and then converted into an effective focal length using Equation (7). The phase method results are shown in Fig. 9. Comparison of these results with those in Fig. 2 (intensity method) shows that the two methods (intensity and phase) are in excellent agreement. The two data sets are collated in Fig. 10 as a parametric plot, showing a close linear relationship with slope of 1. The poor agreement at long focal lengths (low rotational speeds and low pipe-wall temperatures) is probably because a weak gas lens forms in a beam with a large Rayleigh range, thus increasing the uncertainty in beam waist location. Returning to the empirical law of Equation (2), we compare the phase and intensity methods in their respective predictions (see Table 1). The two methods agree within experimental uncertainty. This validates the single measurement wavefront approach, using the phase method. The advantage of this new approach to measuring the properties of an SPGL is that all the propagation parameters and aberrations can be determined by a single measurement.

Conclusion
This study approaches the SPGL from a new perspective, incorporating the full laser beam propagation through the system and the resulting wavefront changes. A CFD numerical model has shown that the pipe ends contribute significantly to overall focusing, and future work could exploit this new CFD model to determine the wavefront aberrations expected from an SPGL. A direct measurement of the wavefront of the laser beam after the SPGL, using a Shack–Hartmann wavefront sensor, confirms the lensing capability of the gas lens, and is in good agreement with previous intensity-based methods. An analytical equation relating the focal length to the measurable waist position has been derived, and should serve as a preliminary starting point for future research on such lenses.
1. Siegman A.E. (1999). Laser beams and resonators: The 1960s. IEEE J. Special Topics Quant. Elect. 20(5), 100–108. [ Links ]
2. Marcuse D. (1965). Theory of a thermal gradient gas lens. IEEE Trans. Microwave Theory Technol. MMT-13(6), 734–739. [ Links ]
3. Steier W.H. (1965). Measurements on a thermal gradient gas lens. IEEE Trans. Microwave Theory Technol. MMT-13(6), 740–748. [ Links ]
4. Gloge D. (1967). Deformation of gas lenses by gravity. Bell Sys. Tech. J. 46(2), 357–365. [ Links ]
5. Kaiser P. (1967). Measured beam deformations in a guide made of tubular gas lenses. Bell Sys. Tech. J. 47, 179–194. [ Links ]
6. Michaelis M.M., Kuppen M., Prause A., Forbes A., Viranna N. and Lisi N. (1996). Progress with gas lenses. Laser & Particle Beams 14(3), 473–485. [ Links ]
7. Aoki Y. and Suzuki M. (1967). Imaging property of a gas lens. IEEE Trans. Microwave Theory Technol. MMT-15(1), 2–8. [ Links ]
8. Ghatak A.K., Malik D.P.S. and Goyal I.C. (1973). Electromagnetic wave propagation through a gas lens. J. Mod. Optics 20(4), 303–312. [ Links ]
9. Martynenko O.G. (1975). Aerothermooptics. Int. J. Heat Mass Transf. 18, 793–796. [ Links ]
10. Michaelis M.M., Forbes A., Conti A., Nativel N, Bencherif H., Bingham R., Kellet B. and Govender K. (2006). Non-solid, non-rigid optics for high power laser systems. In Proc. High Power Laser Ablation VI, SPIE, Bellingham, ed. Claude R. Phipps, 6261, pp. 626115. Taos, New Mexico. [ Links ]
11. Michaelis M.M., Notcutt M. and Cunningham P.F. (1986). Drilling by a gas lens focused laser. Opt. Commun. 59, 369–374. [ Links ]
12. Michaelis M.M., Cunningham P.F., Cazalet R.S., Waltham J.A. and Notcutt M. (1991). Gas lens applications. Laser & Particle Beams 9(2), 641–651. [ Links ]
13. Michaelis M.M., Notcutt M., Cunningham P.F. and Waltham J.A. (1988). Spinning pipe gas lens. Opt. Laser Technol. 20(5), 243–250. [ Links ]
14. Michaelis M.M., Dempers C.A., Kosch M., Prause A., Notcutt M., Cunningham P.F. and Waltham J.A. (1991). A gas lens telescope. Nature 353, 547–548. [ Links ]
15. Forbes A. (1997). Photothermal refraction and focusing, pp. 6, 124–142. Ph.D. thesis, University of Natal, Durban. [ Links ]
16. Mafusire C (2006). Gas lensing in a heated rotating pipe, pp. 24–28, 50. M.Sc. thesis, University of Zimbabwe, Harare. [ Links ]
17. Gerrard A. and Burch J.M. (1975). Matrix Methods in Optics, pp. 57, 149, 156. John Wiley, London. [ Links ]
18. Mafusire C., Forbes A., Snedden G.C. and Michaelis M.M. (2007). Characterisation of a spinning pipe gas lens using a Shack–Hartmann wavefront sensor. In Proc. Laser Beam Shaping VIII, SPIE, Bellingham, eds F.M. Dickey and D.L. Shealy, 6663, pp. 66630H, San Diego, CA. [ Links ]
19. Mafusire C., Forbes A., Michaelis M.M. and Snedden G.C. (2008). Optical aberrations in a spinning pipe gas lens. Optics Express 16(13), 9850–9856. [ Links ]
20. Davison L. (2003). An Introduction to Turbulence Models. Chalmers University of Technology. Online: www.tfd.chalmers.se/~lada/postscript_files/kompen dium_turb.pdf [ Links ]
Received 12 February. Accepted 15 June 2008.
* Author for correspondence. E-mail: aforbes1 @ csir.co.za