Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.7-8 Pretoria Sep./Aug. 2008
REVIEW ARTICLES
Particle acceleration with lasers
Heinrich Schwoerer
Laser Research Institute, Department of Physics, University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa. E-mail: heso@sun.ac.za
ABSTRACT
Within less than a decade, scientists have learned how to use high-intensity lasers to accelerate electrons within a few millimetres to 1 GeV and how to produce ultrashort pulsed proton beams with extremely small emittances. Laser science has touched upon applications in accelerator and synchrotron physics, in hot dense matter and nuclear physics, and one has started to speculate on the feasibility of hitherto experimentally inaccessible nonlinear quantum electrodynamical effects like, for example, photon–photon scattering. Today's acceleration of charged particles by lasers has evolved from the large programmes on inertial confinement fusion that have long been conducted in France and the United States. As fusion laser installations have grown to the size of several soccer fields, however, they place limits on the flexibility of systematic fundamental research. But with the advent of compact, ultra-intense and ultrashort pulsed laser systems, the field of relativistic laser plasma physics has exploded in recent years.
Fields and intensities
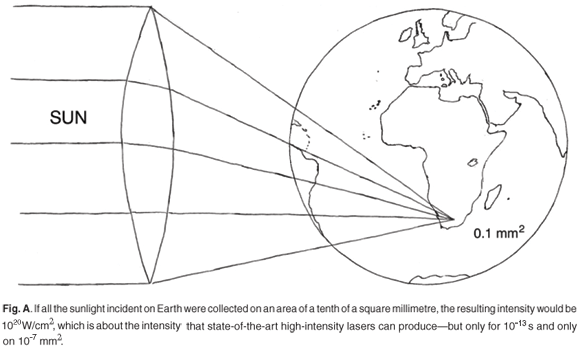
The strength of the electric field in the focus of today's most powerful lasers exceeds 1013 V/m, almost a thousand times greater than the field which binds the electron to the proton in the hydrogen atom. The corresponding light intensity allows for an astonishing analogy: if all the sunlight incident on Earth was focused by means of a huge lens onto the tip of a pencil, the intensity would be more than 1020 W/cm2, which is what today's best lasers can achieve (Fig. A in supplementary material online). From this analogy, however, one immediately sees that for simple energy reasons this intensity cannot be sustained for long, not even over an area the size of a pencil tip. It is generated for a typical duration of 10–13 s onto an area of less than 100 µm2. The pressure of the light on a solid target thereby exceeds many gigabars and matter is heated to millions of degrees. In these laser-generated plasmas, currents are driven to densities of 1012 A/cm2 and magnetic fields of thousands of tesla are generated. Conditions and fields of that magnitude exist in the interior of stars, at the edge of black holes or in galactic jets. The primary process in the interaction of such a light field with matter is the acceleration of electrons. It is this behaviour, together with its implications for science, that I wish to outline in this review.
I will begin with a short account of the technology involved in order to provide an appreciation for the size and nature of a high-intensity laser laboratory. I then introduce some basic theoretical concepts, illustrate the state of the art of laser electron accelerators, and close with reference to the emerging applications involving synchrotrons, ion accelerators and particle colliders.
High-intensity lasers
There are two classes of laser systems capable of generating intensities of 1020 W/cm2 and higher. Historically, the first were high-energy lasers developed around inertial confinement fusion physics. These installations are the size of a small facility, based on flash lamp pumped glass laser technology. Their petawatt versions deliver about a kilojoule of pulse energy within a pulse duration of one picosecond. They can be fired a few times per hour and achieve a reasonable beam quality that can be focused at a maximum intensity of 1021 W/cm2. The only system of this type currently operating is the Vulcan PetaWatt laser at the Rutherford Appleton Laboratory in the U.K.1
The second class are ultrashort-pulse lasers, which were derived from ultrafast spectroscopy. They fit on a few optical tables (and so are called table-top lasers), generate only a few joules of pulse energy, within less than 100 femtoseconds in perfectly focusable beams, and they can be fired at least 10 times a second.2 With the advent of these compact, medium-cost, high-intensity lasers about ten years ago, the field of acceleration of particles by laser has gained momentum. Today, some ten laboratories worldwide, most of them in Europe and the U.S., actively contribute to and compete in the exploration of what is now called relativistic laser plasma physics.
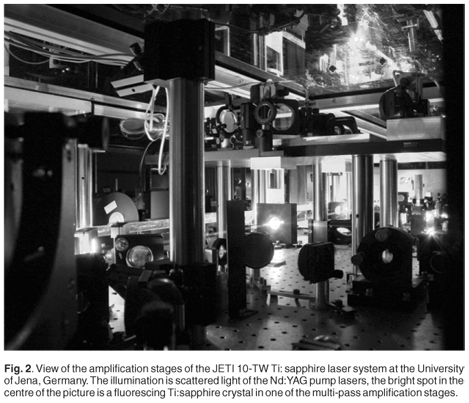
All high-intensity lasers rely on the technology of chirped pulse amplification, a concept that was adopted by lasers from microwave technology in the 1980s.3 To begin with, a mode-locked laser resonator generates ultrashort laser pulses (<10–13 s) with low energy (10–9 J) and a high repetition rate (108 Hz). Some of these pulses are then amplified by a factor of about one billion or more and finally focused onto the smallest possible area. However, the amplified ultrashort pulses inevitably deliver very high intensities onto all adjacent optical surfaces as well as into all materials through which they are transmitted. In order to control optical non-linear processes and avoid damage to the components, the intensity has to be reduced prior to amplification by increasing beam diameter and pulse duration in a well-controlled manner. Temporal stretching and compression occurs in simple passive optical setups. These consist of reflection gratings and telescopes, in which the different spectral components of the ultrashort pulses travel different optical pathlengths, as depicted in Fig. 1.

The amplification mechanism established between stretching and compression is stimulated emission in a laser-active medium, which is typically either a glass, doped with rare earth ions, or a sapphire crystal doped with Ti3+ ions. In the case of Ti:sapphire lasers, the population inversion of the laser-active medium is typically generated by means of frequency-doubled Nd:YAG lasers. Because of the large spectral bandwidth of the laser transition in Ti:sapphire and the high damage threshold upon optical irradiation, these crystals are excellent for the generation of ultrashort laser pulses as well as for their amplification. The first amplification stage typically makes use of a regenerative amplifier, which is itself a Ti:sapphire laser cavity. The pulse to be amplified is seeded into the cavity by means of a fast Pockels cell and a polarizer. It undergoes several round trips until the amplification is saturated and is then switched out again. Within the regenerative amplifier the first six orders of magnitude in amplification is achieved, from nanojoule to millijoule per pulse. Despite the large amplification factor, the spatial mode profile stays almost ideal owing to the geometry of the resonator geometry. The amplifiers employed subsequently are multi-pass Ti:sapphire setups (see Fig. 1). The pulse energy can increase to several joules. Finally, the pulses are compressed down to almost their original duration in the vacuum compressor. Typical parameters are pulse energies of several joules and pulse duration between 30 and 100 fs—corresponding to peak powers of several tens of terawatts—a central wavelength of 800 nm and a shot repetition rate of 10 Hz. The laser pulse now is a disk of light with a diameter of about 50 mm, but only 20 µm thin, even thinner than the paper you hold in your hand.
The intensity in the compressed pulse is already so high that the nonlinear dispersion of the air will destroy its spectrum and its wave front. The laser pulse therefore has to propagate in vacuum, starting with the input of the compressor. The final focusing has to be done with parabolic mirrors as they have neither chromatic nor spherical aberrations. Today's table-top Ti:sapphire lasers generate intensities of up to 1020 W/cm2 averaged over the area of the focal spot. These lasers fit on an area of about 10 m2, require electrical power of the order of 20 kW and are relatively simple to operate. They can be used as work horses in day-to-day experiments and can be run by a competent Ph.D. student in addition to his or her own experiments.
Interaction between laser and matter at relativistic intensities
In the electromagnetic field of the laser, the energy gain of an electron within one atomic diameter exceeds the binding energy of the outer electron shells. The dominant ionization mechanism is therefore field ionization. To a very good approximation, we start with the interaction of these strong laser pulses with free electrons within a plasma. We then proceed in three steps: first, the interaction of an electron with a plane wave, subsequently we introduce the spatial confinement of the focused laser beam, and finally we transfer the process into a plasma.4
We start with the free electron in a weak and plane electromagnetic wave. Its duration is long compared with its period, ensuring that the phase of the carrier wave underneath the envelope can be neglected (the slowly varying envelope approximation). The electron experiences the Lorentz force 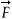 L = e(
L = e(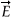 +
+ 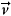 ×
× 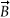 , with e being the charge on the electron and ν its velocity, and
, with e being the charge on the electron and ν its velocity, and  and
and  the electric and magnetic fields, respectively. The electron oscillates along the direction of the electric field
the electric and magnetic fields, respectively. The electron oscillates along the direction of the electric field  with velocity ν = eE / mωcosωt, with m being the electron mass and ω the laser frequency of about 2π·4·1014 Hz. Once the laser pulse has passed the electron, it is at rest again.5
with velocity ν = eE / mωcosωt, with m being the electron mass and ω the laser frequency of about 2π·4·1014 Hz. Once the laser pulse has passed the electron, it is at rest again.5
With increasing electric field strength, the electron's velocity approaches the speed of light c. Now the magnetic part of the Lorentz force 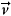 ×
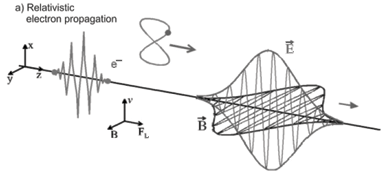
× 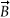 becomes important: electrons are also accelerated in the direction of laser propagation as determined by the cross product. The solution of the relativistic equation of motion results in an additional longitudinal momentum, which oscillates with the doubled laser frequency. The motion of free electrons in a strong field is therefore zig-zag shaped, as seen in Fig. 3a. As the motion is anharmonic, electrons emit radiation at multiples of the laser frequency, a phenomenon called nonlinear Thomson scattering. For our simplified plane wave situation, however, the electron comes to rest after the laser pulse has passed over it. It was translated only a little in the direction of laser propagation and has not gained energy irreversibly.
becomes important: electrons are also accelerated in the direction of laser propagation as determined by the cross product. The solution of the relativistic equation of motion results in an additional longitudinal momentum, which oscillates with the doubled laser frequency. The motion of free electrons in a strong field is therefore zig-zag shaped, as seen in Fig. 3a. As the motion is anharmonic, electrons emit radiation at multiples of the laser frequency, a phenomenon called nonlinear Thomson scattering. For our simplified plane wave situation, however, the electron comes to rest after the laser pulse has passed over it. It was translated only a little in the direction of laser propagation and has not gained energy irreversibly.
The ponderomotive force
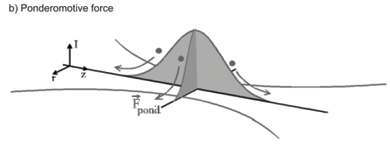
To accelerate the electron irreversibly, we have to leave the symmetry of the plane wave and we do that by considering the real case of a focused laser beam (see Fig. 3b). Solving the same equations of motion for a spatially confined electric field—such as a focused Gaussian beam—results in the so-called ponderomotive force, 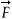 pond ∝ –
pond ∝ – 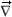 I ∙ λ2, which is proportional to the negative gradient of the intensity.6 Electrons are displaced radially from the laser beam. Imagine an electron starting on the optical axis: it will be accelerated outwards in the first half of the wave. At its turning point, however, the field is weaker and it will not reach its starting point again, but is again displaced outwards during the next cycle, and so on. Eventually, it leaves the laser beam with high velocity. For I = 1020 W/cm2, an electron initially resting in the centre of the beam achieves a final kinetic energy of about 5 MeV. Owing to the relatively broad distribution of the initial positions, however, the overall electron energy spectrum will be very broad.
I ∙ λ2, which is proportional to the negative gradient of the intensity.6 Electrons are displaced radially from the laser beam. Imagine an electron starting on the optical axis: it will be accelerated outwards in the first half of the wave. At its turning point, however, the field is weaker and it will not reach its starting point again, but is again displaced outwards during the next cycle, and so on. Eventually, it leaves the laser beam with high velocity. For I = 1020 W/cm2, an electron initially resting in the centre of the beam achieves a final kinetic energy of about 5 MeV. Owing to the relatively broad distribution of the initial positions, however, the overall electron energy spectrum will be very broad.
The mechanisms described work best at the highest intensity, which is at the focus of the laser beam. As a result of the fundamental diffraction of light, however, the numerical aperture of the focusing limits the focal volume: the shorter the transverse focal area, corresponding to high intensity, the shorter also the focal length (Rayleigh length), and therefore the acceleration distance. An elegant way of increasing the focal length is self-focusing in a homogeneous plasma by the ponderomotive force. It displaces the electrons radially along the optical axis and generates a channel of low electron density. Owing to the density dependence of the refractive index of a plasma, this channel acts like a positive lens on the laser beam. In combination with further ionization and diffraction, this can lead to filamentation of the beam over long distances and therefore a long acceleration length.
Wake field acceleration
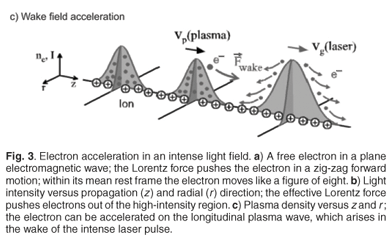
With our knowledge of free electrons, we now consider a strong laser pulse propagating through a plasma. At first, the ponderomotive force pushes electrons forward until the laser pulse overtakes them and pushes them backwards. Because the ions are relatively inert due to their higher mass, this introduces a longitudinal variation in charge density, which can be resonantly driven if the laser pulse duration is just half of the period of the plasma oscillation at the given plasma density. In total, a longitudinal plasma wave develops whose phase travels with the group velocity of the laser pulse behind the laser pulse (Fig. 3c). Electrons can be accelerated in the density wave. As the situation is similar to the wake behind a boat moving through water, this process is called wake field acceleration. Ideally, electrons are injected into the front flank of the wave with high forward velocity and leave before the wave overtakes them.6
If the laser-produced resonant plasma wave is strongly driven, the energy distribution of accelerated electrons can be very narrow, a process which has an analogy with water waves: in a low-amplitude water wave, only the phase of the wave propagates forward, whereas the water molecules simply cycle around their position. However, if the contrast of the wave is high and if it finally breaks, some of the water molecules are captured by the rolling wave front and dragged along until they finally run out of phase and are stopped again. Similarly, if the plasma wave is strongly driven, an electron void develops on the front flank. Some electrons stream into this 'bubble' from behind and are all accelerated to the same kinetic energy. This mechanism, which is sometimes called bubble acceleration, was first predicted by numerical simulation in 20027 and later demonstrated experimentally by three groups in the U.K., France and the U.S. in 2004.8
Experimental results
Electron beams
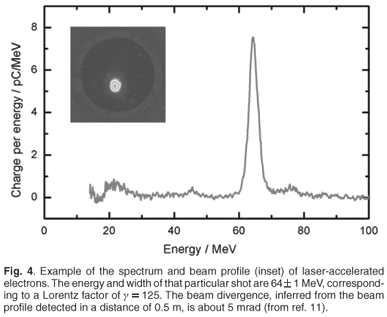
Today's energy record of an electron beam of more than 1 GeV is held by a group in Berkeley, California.9 As the acceleration length is only a few millimetres, the acceleration amounts to several 100 GeV/m. This is higher than in a conventional radiofrequency (RF) accelerator by more than three orders of magnitude. Whereas RF accelerators are limited by material breakdown, leading to ionization, the plasma acceleration described requires ionization and therefore the electric fields can be much higher. The relative spectral width is in the order of a per cent, the beam divergence around one mrad. The duration of the electron pulse is shorter than 100 fs and can contain up to 109 particles.
Interesting applications of these laser-accelerated electrons can arise in X-ray and nuclear physics. If the electrons are stopped in a high-Z material like tungsten or tantalum, ultrashort pulses of hard X-rays and γ-rays are produced within a very small volume. In recent years all elementary nuclear reactions as well as cross-section measurements with these ultrashort pulses of high-energy radiation were successfully demonstrated, including (γ, n)-, (γ, p)- and fusion reactions.10
At present the acceleration length is limited to a few millimetres. Because the fundamental electron acceleration process is well understood, however, it seems to be feasible to increase the electron energy much more in the future by staging several accelerations. By that means laser acceleration experiments gradually approach typical accelerator applications such as the generation of synchrotron radiation, free electron lasers and collision experiments.
Synchrotron radiation
One of the best-established scientific applications of RF electron accelerators is the generation of narrowband and tunable synchrotron radiation in the ultraviolet to soft X-ray spectral range. X-ray structural analysis by diffraction of synchrotron radiation, for example, is an extremely powerful method in physics, chemistry, biology and materials science. However, the method is limited to stationary, time-independent structures or slow kinetics because the duration of the synchrotron pulse is not shorter than about 100 ps. In contrast, femtosecond lasers deliver light pulses in the temporal range of intramolecular dynamics, but at visible wavelengths and therefore cannot support the microscopic spatial resolution of the synchrotron light source.
An obvious way of combining the two requirements for temporal and spatial resolution at a molecular level is now opened up by laser-accelerated relativistic electrons propagating through a conventional undulator. A first proof of principle experiment was recently performed in a cooperative venture between the Jena group in Germany, the Laser Research Institute in Stellenbosch and the University of Strathclyde in the U.K., where 60-MeV electrons were sent through an undulator and synchrotron light could be successfully detected (see Fig. 5).11 Scaling the results to today's best laser-accelerated electron pulses, synchrotron light in the nanometre range will be generated with a pulse duration of less than 100 fs. As with conventional accelerator facilities, the next step is the generation of coherent undulator radiation through a free-electron laser. This requires electron bunch durations shorter than the period of the radiation generated, which can be accomplished by so-called self-amplified spontaneous emission (SASE): by interaction with the light generated, the initially longer electron pulses decay into a regular series of ultrashort pulses of exactly the required duration. SASE facilitates free electron lasing at the Free Electron Laser (FEL) facilities of DESY in Hamburg, Germany, and ALS in Berkeley, California, and it might also be applicable to accelerators based on laser plasmas.

An application of that novel light source to time-resolved structural analysis still requires improvement in the spatial and spectral stability of the electron beams. However, given the dynamics of the evolution of the field in the last five years and the progress made, I have no doubt that purely laser-driven or all-optical FEL sources will eventually produce tunable short-wavelength, coherent, ultrashort and polarized—in short, brilliant—light pulses for a wealth of applications.
Counter-propagating beams, the photon collider
In the experiments mentioned so far, the laser beam and particle beams were directed towards an analysing detector or a target. However, since a laser beam can easily be split and deflected in any ratio and in any direction by means of beamsplitters and mirrors, two laser pulses can be counter-propagated and collided.12 The so-called photon collider was recently developed at the University of Jena to collide two ultrashort and ultra-intense laser pulses (see Fig. 6). Depending on the positions of the two foci and the matter involved, one can collide the laser photons with photons or with laser-accelerated electrons. Even electron–electron collisions can be considered. For the short time of the collision, the fluxes are extremely high: each laser pulse delivers 1018 photons of 1.5 eV in 10–13 s onto an area of less than 10 µm2 (c. 1038 photons s–1 cm–2), each electron pulse carries up to 109 electrons within the same duration and area (1029 electrons s–1 cm–2).

In the electron–photon collision, the laser-accelerated electrons undulate in the counter-propagating light field. The 'undulator period' is now the wavelength of the light, which is, however, Lorentz contracted from the point of view of the relativistic electron. The energy of scattered light depends on the angle of emission and is highest in the backscattered direction. For 10-MeV electrons, corresponding to a Lorentz factor of γ = 20, easily produced in the photon collider, the backscattered relativistic Thomson radiation is already in the form of hard X-rays with ETh = 4γ2 EL = 2.4 keV. This X-ray pulse is as short as the laser pulse as it can be generated only once the laser pulse and laser-generated electron pulse penetrate each other. Moreover, the relativistic Thomson radiation is a subtle time-resolved diagnostic of the electron acceleration itself, because only once electrons have been accelerated can laser photons scatter off them.13
If both beams accelerate electrons, pairs of electrons and positrons should be generated by electron–electron collisions. With even faster electrons, pairs of heavier and short-lived particles also could be generated and immediately accelerated in the laser field to relativistic energies to extend their life time in the laboratory.
If matter is completely removed from the foci, one can start to speculate about the possibility of polarizing the vacuum.14 Absorption of the electromagnetic energy by the vacuum and emission of an electron–positron pair happens only above the so-called Schwinger field of 1.3 × 1016 V/cm, corresponding to 4.4 × 1029 W/cm2, which is not accessible in the foreseeable future.15 However, dispersive effects like birefringence of the vacuum16 or photon–photon scattering17 could become reality, a regime of nonlinear quantum electrodynamics (QED) at high fields and low energies, which was never experimentally accessible before. The unsuccessful PVLAS experiment in Italy, in which a magnetic field was supposed to change the polarization of light, has demonstrated the great theoretical interest in the topic.18
Finally, laser acceleration of electrons is also the primary process in the present-day laser acceleration of ions, as discussed below.
Ions and protons
With today's laser systems, the ponderomotive force, which is responsible for electron acceleration as described above, is too weak to accelerate protons or heavier plasma ions to relativistic energies. Intensities in the range of 1023 W/cm2 and higher are required. However, if the spatial region of laser plasma interaction and electron acceleration is separated from the region of the charge separation, a remarkable ion acceleration mechanism can be enforced. For that purpose the laser pulse is focused onto a thin metal foil (Fig. 7). In the pre-plasma region in front of the foil, electrons are accelerated, the fastest once again in a forward direction into the metal foil as we have learnt above. On the one hand, the foil must be thin enough to cause insignificant energy loss of the electrons. The fast electrons exit the far side of the foil and build up a sheath of hot electrons. If, on the other hand, the foil is thick enough still to be macroscopically intact once the electrons exit at the rear side, the field between the sheath and the remaining positively charged foil is orientated normal to the foil. Appropriate foil thicknesses lie in the order of a few micrometres. The field can be as high as 100 GV/m or more and it lasts for slightly longer than the delivery of fast electrons, in other words, the duration of the laser pulse. Ions from the rear surface of the foil are accelerated into the vacuum. Because of its geometry, the process is called 'target normal sheath acceleration' (TNSA).19 Ions with the largest charge to mass ratio are accelerated the most. These are usually protons and highly charged carbon ions from surface contaminants. The process generates extremely low transverse emittance ion beams due to the small source size (10 µm diameter), the negligible kinetic energy prior to acceleration, the ultrashort acceleration time (100 fs) and the charge neutrality of the beam. This means that the ion beam is extremely laminar.20
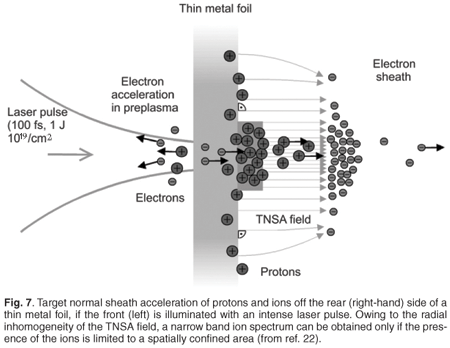
The radial inhomogeneity of the TNSA field causes the photons to display a broad energy spectrum, with a high energy cut-off determined by the laser pulse energy and intensity, and typical values around 5 MeV for table-top laser systems. If one restricts the abundance of protons at the back of the foil to the centre of the TNSA field, however, where it is essentially homogeneous (see Fig. 7), and if these are not too numerous, then all of them experience the same field and potential and their energy spectrum narrows. As for the acceleration of the narrow-band electrons, this effect was suggested theoretically,21 realized experimentally22 and, from the experiments, the theory was refined.23
The excellent beam properties of laser-accelerated ions allows one to think of a variety of applications such as injections into conventional accelerators,24 or the time-resolved probing of hot and dense matter.25 The combination of laser-accelerated protons and the high fields of the laser itself opens up the prospect of investigating nuclear reactions and decay in extreme external fields and high temperature, which are of fundamental interest to astrophysicists. Finally, one may think of the generation of short-lived isotopes using lasers instead of accelerators,26 or even the irradiation of biologically interesting targets with laser-accelerated ions.
| High-intensity laser research in South Africa About four years ago, the vision of a South African High Intensity Laser Facility was conceived at the Laser Research Institute in Stellenbosch. This ambition was introduced to the scientific community through the South African Institute of Physics and immediately attracted the interest of the National Laser Centre and also of the National Research Foundation's iThemba Labs. With the appointment of the author as a South African research professor, the expertise to install and operate such a facility and to contribute to scientific progress in the field is now available in this country. It was therefore decided to follow up the vision within the Photonics Initiative of South Africa (PISA). With this as background, a four-day summer school will be organized in Stellenbosch in January 2009 to introduce the scientific community to the state of high-intensity laser research and to invite interested parties to participate in the project. |
Summary
We have seen how the ponderomotive force of a strong light field, which is nothing other than the light pressure, impels electrons to highly relativistic energies in well-defined beams and ultrashort pulses. We have also seen how these laser-accelerated electrons can be used to produce ion beams with exceptional qualities. The main message of this review is that the dynamic young field of relativistic laser plasma physics is evolving towards accelerator and nuclear physics, where it will find niche areas through the unique properties of laser-accelerated pulses of particles and radiation as well as benefiting from the compactness of the equipment. There is just a small number of research groups involved, so that many of the interesting applications are typically only touched upon and then abandoned in favour of the next exciting topic. These developments certainly expand the mind and are bearing fruit, but some of the visions and promises will be possible only with the availability of beam time on 50-TW class lasers. The future will also bring even more powerful laser systems, able to push ions to relativistic energies and to approach experimentally some of the nonlinear QED proposals. From the success of today's table-top lasers, however, we have learned that scientific benefits are achieved by the most flexible and creative experimental approach rather than the most powerful laser.
1. Danson C., Brummitt P., Clarke R., Collier J., Fell B., Frackiewicz A., Hancock S., Hawkes S., Gomez C.H., Holligan P., Hutchinson M., Kidd A., Lester W., Musgrave I. Neely D., Neville D., Norreys P., Pepler D., Reason C., Shaikh W., Winstone T., Wyatt R. and Wyborn B. (2004). Vulcan Petawatt – an ultra-high-intensity interaction facility. Nuclear Fusion 44(12), S239–S246. [ Links ]
2. Chériaux G. and Chambaret G. P. (2001). Ultra-short high-intensity laser pulse generation and amplification. Measurement Science and Technology 12, 1769–1776. [ Links ]
3. Strickland D. and Mourou G. (1985). Compression of amplified chirped optical pulses. Optics Commun. 56, 219–221. [ Links ]
4. Schwoerer H. (2006). Surfen auf dem Laserstrahl. Physik J. 5, 25–31. [ Links ]
5. Amiranoff F. (2001). Fast electron production in ultra-short high-intensity laser-plasma interaction and its consequences. Measurement Science and Technology 12, 1795–1800. [ Links ]
6. Kruer W. (1988). The Physics of Laser Plasma Interactions. Addison Wesley, New York. [ Links ]
7. Pukhov A. and Meyer-ter-Vehn J. (2002). Laser wake field acceleration: the highly non-linear broken-wave regime. Appl. Phys. B 74, 355–361. [ Links ]
8. Mangles S., Murphy C., Najmudin Z., Thomas A., Collier J., Dangor A., Divall E., Foster P., Gallacher J., Hooker C., Jaroszynski D., Langley A., Mori W., Norreys P., Tsung F., Viskup R., Walton B. and Krushelnick K. (2004). Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 431, 535–538; and Geddes C., Toth C., van Tilborg J., Esarey E., Schroeder C., Bruhwiler D., Nieter C., Cary J. and Leemans W. (2004). High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 431, 538–541; and Faure J., Glinec Y., Pukhov A., Kiselev S., Gordienko S., Lefebvre E., Rousseau J., Burgy F. and Malka V. (2004). A laser-plasma accelerator producing monoenergetic electron beams. Nature 431, 541–544. [ Links ]
9. Leemans W., Nagler B., Gonsalves A., Toth C., Nakamura K., Geddes C., Esarey E., Schroeder C. and Hooker S. (2006). GeV electron beams from a centimetre-scale accelerator. Nature Physics 2, 696–699. [ Links ]
10. Schwoerer H., Magill J. and Beleites B. (2006). Lasers and Nuclei, Applications of High Intensity Lasers in Nuclear Science. Lecture Notes in Physics 694, Springer, Berlin, and references therein. [ Links ]
11. Schlenvoigt H., Haupt K., Debus A., Budde F., Jäckel O., Pfotenhauer S., Schwoerer H., Rohwer E., Gallacher J., Brunetti E., Shanks R., Wiggins S. and Jaroszynski D. (2007). A compact synchrotron radiation source driven by a laser-plasma wakefield accelerator. Nature Physics 4, 130–133; and K. Nakajima (2008). Towards a table-top free electron laser. Nature Physics 4, 92. [ Links ]
12. Liesfeld B., Bernhardt J., Amthor K., Schwoerer H. and Sauerbrey R. (2005). Single-shot autocorrelation at relativistic intensity. Appl. Phys. Lett. 86, 161107 1–3. [ Links ]
13. Schwoerer H., Liesfeld B., Schlenvoigt H., Amthor K. and Sauerbrey R. (2006). Thomson-backscattered X rays from laser-accelerated electrons. Phys. Rev. Lett. 96, 014802 1–4. [ Links ]
14. Marklund M. and Shukla P. (2006). Nonlinear collective effects in photon–photon and photon–plasma interactions. Rev. Mod. Phys. 78, 591–640. [ Links ]
15. Schwinger J. (1951). On gauge invariance and vacuum polarization. Phys. Rev. 82, 664–679. [ Links ]
16. Heinzl T., Liesfeld B., Amthor K., Schwoerer H., Sauerbrey R. and Wipf A. (2006). On the observation of vacuum birefringence. Optics Commun. 267, 318– 321. [ Links ]
17. Lundström E., Brodin G., Lundin J., Marklund M., Bingham R., Collier J., Mendonca J. and Norreys P. (2006). Using high-power lasers for detection of elastic photon–photon scattering. Phys. Rev. Lett. 96, 1–4. [ Links ]
18. Zavattini E., Zavattini G., Ruoso G., Polacco E., Milotti E., Karuza M., Gastaldi U., Di Domenico G., Della Valle F., Cimino R., Carusotto S., Cantatore G. and Bregant M. (2006). Experimental observation of optical rotation generated in vacuum by a magnetic field. Phys. Rev. Lett. 96, 110406, 1–4; and same authors, Editorial Note: Experimental observation of optical rotation generated in vacuum by a magnetic field [Phys. Rev. Lett. 96, 110406 (2006)]. Phys. Rev. Lett. 99, 129901 (2007). [ Links ]
19. Wilks S., Langdon A., Cowan T., Roth M., Singh M., Hatchett S., Key M., Pennington D., MacKinnon A. and Snavely R. (2001). Energetic proton generation in ultra-intense laser-solid interactions. Physics of Plasmas 8, 542. [ Links ]
20. Borghesi M., Mackinnon A., Campbell D., Hicks D., Kar S., Patel P., Price D., Romagnani L., Schiavi A. and Willi O. (2004). Multi-MeV proton source investigations in ultraintense laser–foil interactions. Phys. Rev. Lett. 92 (5), 055003 1–4; and Cowan T.E., Fuchs J., Ruhl H., Kemp A., Audebert P., Roth M., Stephens R., Barton I., Blazevic A., Brambrink E., Cobble J., Fernandez J., Gauthier J., Geissel M., Hegelich M., Kaae J., Karsch S., Sage G.P.L., Letzring S., Manclossi M., Meyroneinc S., Newkirk A., Pepin H. and LeGalloudec N.R. (2004). Ultralow emittance, multi-MeV proton beams from a laser virtual-cathode plasma accelerator. Phys. Rev. Lett. 92, 204801 1–4. [ Links ]
21. Esirkepov T., Bulanov S., Nishihara K., Tajima T., Pegoraro F., Khoroshkov V., Mima K., Daido H., Kato Y., Kitagawa Y., Nagai K. and Sakabe S. (2002). Proposed double-layer target for the generation of high quality laser accelerated ion beams. Phys. Rev. Lett. 89(17), 175003 1–4. [ Links ]
22. Schoerer H., Pfotenhauer S., Jäckel O., Amthor K., Liesfeld B., Ziegler W., Sauerbrey R., Ledingham K. and Esirkepov T. (2006). Laser–plasma acceleration of quasi-monoenergetic protons from microstructured targets. Nature 439, 445–448. [ Links ]
23. Robinson A. and Gibbon P. (2007). Production of proton beams with narrow-band energy spectra from laser-irradiated ultrathin foils. Phys. Rev. E 75 015401 1–4. [ Links ]
24. Roth M., Cowan T.E., Key M.H., Hatchett S.P., Brown C., Fountain W., Johnson J., Pennington D.M., Snavely R.A., Wilks S.C., Yasuike K., Ruhl H., Pegoraro F., Bulanov S.V., Campbell E.M., Perry M.D. and Powell H. (2001). Fast ignition by intense laser-accelerated proton beams. Phys. Rev. Lett. 86, 436–439. [ Links ]
25. Borghesi M., Romagnani L., Schiavi A., Campbell D., Haines M., Willi O., Mackinnon A., Galimberti M., Gizzi L., Clarke R. and Hawkes S. (2003). Measurement of highly transient electrical charging following high-intensity laser–solid interaction. Appl. Phys. Lett. 82, 1529–1531. [ Links ]
26. Ledingham K.W.D., McKenna P., McCanny T., Shimizu S., Yang J.M., Robson L., Zweit J., Gillies J.M., Bailey J., Chimon G.N., Clarke R.J., Neely D., Norreys P.A., Collier J.L., Singhal R.P., Wei M.S., Mangles S.P.D., Nilson P., Krushelnick K. and Zepf M. (2004). High power laser production of short-lived isotopes for positron emission tomography. J. Phys. D: Appl. Phys. 37, 2341–2345. [ Links ]
Received 11 December 2007. Accepted 4 July 2008.
This article is accompanied by a supplementary figure online at www.sajs.co.za
Schwoerer H. (2008). Particle acceleration with lasers. S. Afr. J. Sci. 104, 299-304.