Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.5-6 Pretoria May./Jun. 2008
BIOLOGICAL MODELLING
A model of HIV infection with two viral strains and cytotoxic T-lymphocyte response under structured treatment interruptions
R. OuifkiI; A. WelteII, *; C. PretoriusI
IDST/NRF Centre of Excellence in Epidemiological Modelling and Analysis (SACEMA), Stellenbosch University, Stellenbosch 7600, South Africa
IIDST/NRF Centre of Excellence in Epidemiological Modelling and Analysis (SACEMA), Stellenbosch University, Stellenbosch 7600; and School of Computational and Applied Mathematics, University of the Witwatersrand, Private Bag 3, WITS 2050, South Africa
ABSTRACT
We develop a model of HIV infection with two viral strains, a cytotoxic T-lymphocyte (CTL) response and structured treatment interruptions. We derive new analytical relations characterizing the dynamics between drug-sensitive and drug-resistant variants of the virus, and the strength of the CTL response.
Introduction
Many mathematical models have been developed to describe the dynamics of HIV replication under antiretroviral treatment (ART) and the emergence of resistant mutants. ART has frequently been shown to reduce the viral load to undetectable levels, but ART regimens are complex and difficult to adhere to, and the drugs are toxic with long-term side effects (see e.g. refs 1–8.).
Structured treatment interruptions (STIs), that is, periodic (cyclical) interruptions in ART, are being explored as an alternative strategy to continuous ART, as, in addition to reducing side effects, they may also serve to boost HIV-specific immune responses (see e.g. refs 9–11). Nevertheless, STIs also carry the serious risk of improper viral control. Long periods without treatment allow the viral population to grow, potentially causing too much 'stimulation', leading ultimately to immune system deterioration and AIDS.
In this paper we explore viral strain dynamics by developing a mathematical model that includes a simple viral life cycle, the effects of periodic treatment (including interruptions) and an immune system response in the form of cytotoxic T-lymphocytes (CTLs). We derive new conditions to characterize the dynamics of this system under conditions that simulate possible STI strategies.
The paper is organized as follows: We first provide a brief analysis of the basic model of HIV infection. Next, we extend the analysis to include two viral strains and treatment with a reverse transcriptase inhibitor (RTI), possibly with STIs. We investigate the stability of the steady states and establish a condition for a switch between the dominance of the two strains of HIV. This demonstrates how the treatment interruptions relate to drug resistance in this model. Finally, we include an immune system response (in particular of CTLs) and explore how CTL level varies under the influence of the STI. The appendix contains proofs for the propositions presented in the body of the paper.
The basic model of HIV infection with reverse transcriptase inhibitor
HIV is an RNA virus. When it infects a cell, the enzyme reverse transcriptase (RT) makes a DNA analogue of its RNA genome, which is integrated into the DNA of the infected cell. RTIs reduce infection by inhibiting the action of reverse transcriptase. A model that accounts for the action of an RTI is (see e.g. refs 12–14).

where T denotes the population of uninfected/target cells (mostly CD4+ T cells), Y represents the population of infected cells, and V the virus particle (virion) population. Here it is assumed that target cells are created at a constant rate λ, die at a rate d per cell and are infected at constant mass action rate k, under perfect mixing of healthy and infected cells. Infected cells, Y, die at a rate δ per cell and virions are produced by productively infected cells. The form of the equations assumes that on average each productively infected cell produces N virions during its lifetime. Free virions are assumed to be cleared at rate c per virion. The efficacy of the RTI is captured by ε; if ε = 1, the inhibition is 100% effective, whereas if ε = 0, there is no inhibition.
Using the method of linearization and the Ruth-Hurwitz criterion, one can easily show that depending on the efficacy of the parameters, either the system eliminates the virus or the viral load will stabilize at a non-zero steady state.
Accounting for two strains of HIV and structured treatment interruptions
In the previous model, only one strain of virus was considered. In reality, chemical 'errors' occur in the HIV life cycle (especially during transcription between RNA and DNA), leading to different strains of HIV, Vi. A target cell which is infected by the strain i is denoted by Yi. Numerous mathematical models for HIV infection that account for more than one strain have been developed (see e.g. ref. 3). A model accounting for two strains is as follows:

where εi(t) represents the efficacy of the drug on the strain Vi and ηi is the rate of mutation of the strain Vi. The infection and viral production rates are also allowed to vary between strains.
In dynamical models of infection, whether of individuals or cells, it is usually instructive to obtain expressions for the basic reproductive number (R0), which is the average number of new infections spawned by a single infected individual (or cell) inserted into an otherwise healthy population. In the case of a constant drug efficacy (εi(t) = εi), we have

where
Λ = ((1- η2) 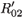 - (1 - η1)
- (1 - η1)  )2 + 4η1η2
)2 + 4η1η2 
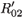
and
 (i = 1, 2);
(i = 1, 2);
with  = ki (1 - εi). Moreover:
= ki (1 - εi). Moreover:
1) If R0 < 1, then system (2) has only one steady state, the virus-free steady state, (
, 0, 0, 0, 0) which is locally asymptotically stable.
2) If R0 > 1, then the virus-free steady state becomes unstable and system (2) has one additional steady state, the infected steady state.
When two viral strains are not identical, it would require fine tuning of the underlying parameters to obtain equal values for img02 and img01. So the natural case is  ≠
≠ 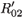 and then the infected steady state is given by
and then the infected steady state is given by

If the underlying parameters for the two strains are somehow adjusted to give  =
= 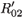 , then the equilibrium condition is given by
, then the equilibrium condition is given by

Let 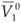 and
and  be the values of V1 and V2 at the equilibrium in the absence of RTI therapy. Under the influence of RTI therapy, there will be a switch between the two strains if [(
be the values of V1 and V2 at the equilibrium in the absence of RTI therapy. Under the influence of RTI therapy, there will be a switch between the two strains if [(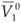 –
–  ) (
) (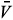 1 –
1 – 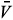 2) < 0] with ((
2) < 0] with ((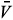 1 ≠
1 ≠ 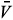 2). We obtain a precise necessary and sufficient condition for this switch between the two strains. Denote
2). We obtain a precise necessary and sufficient condition for this switch between the two strains. Denote
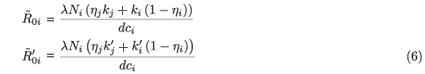
where j = 2 if i = 1 and j = 1 if i = 2. 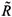 0i (conversely
0i (conversely  ) represents the basic reproductive number of strain i, accounting for mutations, but without treatment (conversely under RTI treatment). To talk clearly about a switch between two conditions, we assume that
) represents the basic reproductive number of strain i, accounting for mutations, but without treatment (conversely under RTI treatment). To talk clearly about a switch between two conditions, we assume that  ≠
≠ 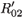 and
and  ≠
≠ 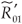 . There is a switch between the two strains if and only if
. There is a switch between the two strains if and only if

If we consider a treatment with periodic efficacy, system (2) has only one steady state, the virus-free steady state, ( , 0, 0, 0, 0). Assume that εi(t) is periodic and is given by a finite Fourier series:
, 0, 0, 0, 0). Assume that εi(t) is periodic and is given by a finite Fourier series:

where  is the mean value of εi(t). Denote by
is the mean value of εi(t). Denote by  0 the basic reproductive number of the averaged system of (2) (i.e. calculated for εi (t) =
0 the basic reproductive number of the averaged system of (2) (i.e. calculated for εi (t) =  , the mean value of εi(t)). In this case, is given by Equation (3) where εi is replaced by
, the mean value of εi(t)). In this case, is given by Equation (3) where εi is replaced by  . The following result holds: If
. The following result holds: If  0 > 1, then the virus-free steady state is unstable.
0 > 1, then the virus-free steady state is unstable.
If  0>1, the extended system of (2) (see appendix) has an infected steady state which corresponds to the infected steady state of the averaged system (2) (i.e. εi(t) replaced by
0>1, the extended system of (2) (see appendix) has an infected steady state which corresponds to the infected steady state of the averaged system (2) (i.e. εi(t) replaced by  ). Numerical evidence shows that this steady state is stable.
). Numerical evidence shows that this steady state is stable.
We now give an explicit condition for the switch between the two strains in terms of the efficacy of RTI. We adopt the form εi(t)=εi є(t), where εi represents the strain-specific efficacy of RTI and є(t) is a periodic function representing the (strain independent) level of RTI therapy. This naive 'pharmokinetic' model should only be interpreted for physically sensible values of є(t) (i.e. between 0 and 1). Consider the regime 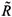 01 >
01 > 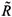 02. The condition for the switch is
02. The condition for the switch is 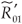 <
<  , which is equivalent to
, which is equivalent to

Assume that the concentration, є1(t), of an RTI, following a single dose can be represented by a generic rise and fall as in Fig. 1. For convenience, we define S+=  є(s)ds as the area under the concentration curve where the level of drug is above what the regimen aims to maintain outside of drug holidays. Similarly, we define
є(s)ds as the area under the concentration curve where the level of drug is above what the regimen aims to maintain outside of drug holidays. Similarly, we define  є(s)ds and
є(s)ds and  є(s)ds to decompose the area under this curve into convenient pieces as building blocks for the periodic case. If we consider a treatment with STIs consisting of n successive doses at equal intervals of time, followed by a period of drug holiday of length Loff, we obtain a form for є1(t) as in Fig. 2. The mean value of this function is given by
є(s)ds to decompose the area under this curve into convenient pieces as building blocks for the periodic case. If we consider a treatment with STIs consisting of n successive doses at equal intervals of time, followed by a period of drug holiday of length Loff, we obtain a form for є1(t) as in Fig. 2. The mean value of this function is given by



We can now give the switch condition in terms of the length of the drug holiday, namely Loff < 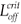 , where
, where

Treatment naturally applies selective pressure on the combined system of the two strains. This condition shows the critical value for the length of the drug holiday below which the STIs will select for drug resistance, in the sense that the resistant strain population exceeds the wild-type viral population. One must consider further details of all the parameters to be able to decide when this is clinically problematic. In the limit of infinite interruptions (i.e. no treatment), there is a tiny drug-resistant population, but also no viral control. In the limit of highly effective continuous treatment, there is strong viral suppression (perhaps even viral elimination, if R0 can be reduced below unity) but the largest sub-population of any remaining virions will be the drug-resistant strain. We do not explore the intermediate regimes in any more detail, as this is only a sensible exercise if we can insert numerous parameter values realistically into physically relevant regimes, and for the present model we cannot do this. It should be noted that the present model is simplistic in the sense that:
- There are only two strains, whereas in reality there are many coexisting strains, and
- the mutation rate we are using is approximately realistic for two strains which differ by a single point mutation. Important pairs of strains in reality may have very low mutation rates, which are not sensibly modelled by continuous dynamics, since mutation events will be rare.
Thus, to explore the emergence of clinically observed drug resistance further, substantially more complex models need to be considered. One might then be able to demonstrate more nuanced hypothetical patient histories, including the appearance of multiple mutations from populations of inadequately suppressed single-point mutants.
Including a CTL response
In this section we extend model (2) by inclusion of a population of effector (E) CD8+ T cells, also known as cytotoxic T-lymphocytes. This cell population is stimulated into clonal expansion in response to HIV infection (see e.g. ref. 15). We obtain the following model:
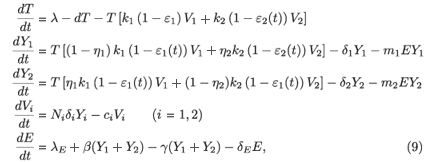
where λE denotes a constant source of effector cells, β(Y1 + Y2) represents the reaction term to the target cell infection, γ(Y1 + Y2) is the loss term due to the binding of effector cells to infected cells, and δE is the clearance rate of effector cells. Using the same analysis as in the previous section, we see that the basic reproductive number of the averaged system associated with (9), (εi (t) =  ), is given by
), is given by
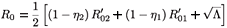
where
Λ = ((1 - η2) 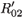 - (1 - η1)
- (1 - η1)  )2 + 4η1η2
)2 + 4η1η2 
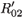
and
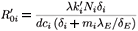 (i - 1, 2),
(i - 1, 2),
with  = ki (1 -
= ki (1 -  ). Moreover, if R0 > 1, then the virus-free steady state
). Moreover, if R0 > 1, then the virus-free steady state 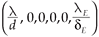 , of (9) is unstable.
, of (9) is unstable.
Unlike system (2), the investigation of infected steady states for system (9) is quite complicated (it involves the roots of a polynomial of 5th order). Nevertheless, one can use a perturbation method to determine the infected steady states. In fact, since η1 and η2 are small (around 10–6), one can determine the infected steady states for η1 = η2 = 0. A straightforward investigation shows that when R0 > 1 (η1 = η2 = 0), there exists a unique infected steady state 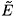 0 (we do not give its expression because we do not need it in our analysis). By means of the implicit function theorem, one can show that for η1 ≈ η2 ≈ 0, there exists an infected steady state
0 (we do not give its expression because we do not need it in our analysis). By means of the implicit function theorem, one can show that for η1 ≈ η2 ≈ 0, there exists an infected steady state 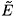 which is close to
which is close to 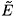 0.
0.
From the last equation of (9), we see that the value of E at the equilibrium is given by

Clearly, if R0 increases, so do  1,
1,  2 and
2 and  .
.
Consider an RTI treatment with STI, εi(t) = εi є(t). In order to increase R0, one needs to decrease the mean value of є(t), which can be achieved by increasing the length of the drug holidays.
Thus, STIs can be used to boost the CTL response by increasing the length of the drug holidays; however, the length of this period must not be so long that loss of viral control results. Uncontrolled viremia will clinically lead to immune system degradation, as well as the more complex viral evolution scenarios already mentioned following Proposition (8), neither of which can be demonstrated in a simple model like ours.
Finally, we adapt the threshold for the switch to having the resistant viral population outnumber the wild type, which is now given by
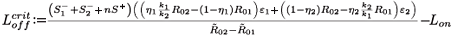
where

1. McLean A.R., Emery V.C., Webster A. and Griffiths P.D. (1991). Population dynamics of HIV within an individual after treatment with zidovudine. AIDS 5, 485–489. [ Links ]
2. Nowak M.A., Anderson R.M., McLean A.R., Wolfs T., Goudsmit J. and May R.M. (1991). Antigenic diversity thresholds and the development of AIDS. Science 254, 963–969. [ Links ]
3. Bonhoeffer S., May R.M., Shaw G.M. and Nowak M.A.(1997). Virus dynamics and drug therapy. Proc. Natl Acad. Sci. USA 94, 6971–6976. [ Links ]
4. McLean A.R. and Nowak M.A. (1992). Competition between zidovudine sensitive and resistant strains of HIV. AIDS 6, 71–79. [ Links ]
5. Frost S.D.W. and McLean A.R. (1994). Quasispecies dynamics and the emergence of drug resistance during zidovudine therapy of HIV infection. AIDS 8, 323–332. [ Links ]
6. Wein L.M., Zenios S. and Nowak M.A. (1997). Dynamic multidrug therapies for HIV: a control theoretic approach. J. theor. Biol. 185, 15–29. [ Links ]
7. Kirschner D.E. and Webb G.F. (1997). Understanding drug resistance for montherapy treatment of HIV infection. Bull. Math. Biol. 59, 763–786. [ Links ]
8. DeBoer R.J. and Boucher C.A.B. (1996). Anti-CD4 therapy for AIDs suggested by mathematical models. Proc. R. Soc. Lond. 263, 899–905. [ Links ]
9. Adams B.M., Banks H.T., Davidian M. and Rosenberg E.S. (2007). Estimation and prediction with HIV-treatment interruption data. Bull. Math. Biol. 69(2), 563–584. [ Links ]
10. Lori F. and Lisziewicz J. (2001). Structured treatment interruptions for the management of HIV infection. J. Am. Med. Assoc. 4286(23), 2981–2987. [ Links ]
11. Bongiovanni M., Casana M., Tincati C. and Monforte A.A. (2006). Treatment interruptions in HIV infected subjects. J. Antimicrobial Chemother. 58, 502–505. [ Links ]
12. Perelson A.S., Neumann A.U., Markowitz M., Leonard J.M. and Ho D.D. (1996). HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271, 1582–1586. [ Links ]
13. Perelson A.S. and Nelson P.W. (1999). Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 41(1), 3–44. [ Links ]
14. Nowak M.A. and May R.M. (2000). Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press, Oxford. [ Links ]
15. Bonhoeffer S., Rembiszewski M., Ortiz G.M. and Nixon D.F. (2000). Risks and benefits of structured antiretroviral drug therapy interruptions in HIV-1infection. AIDS 14, 2313–2322. [ Links ]
16. van den Driessche P. and Watmough J.(2002). Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 80, 29–48. [ Links ]
* Author for correspondence. E-mail: alex.welte@wits.ac.za
Proof of the basic reproductive number and stability analysis for system (2): A steady state ( ,
,  1,
1,  2,
2, 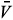 1,
1, 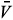 2) of (2) is the solution of
2) of (2) is the solution of
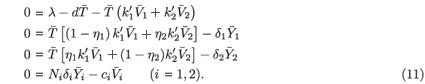
The last equation of (11) implies that 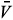 i =
i = 
 i. By substituting this into the second and third equations of (11), we obtain
i. By substituting this into the second and third equations of (11), we obtain 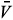 1 =
1 = 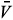 2 = 0, or
2 = 0, or

I. If 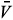 1 =
1 = 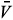 2 = 0, then
2 = 0, then  1 =
1 =  2 = 0 and
2 = 0 and  2 =
2 =  , leading to the virus-free steady state E0 = (
, leading to the virus-free steady state E0 = ( , 0, 0, 0, 0). To determine the basic reproductive number of (2), we use the method described in Watmough and van den Driessche.16 We obtain the expression (3).
, 0, 0, 0, 0). To determine the basic reproductive number of (2), we use the method described in Watmough and van den Driessche.16 We obtain the expression (3).
II. If 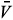 1 =
1 = 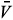 2 ≠ (0, 0), then χ(
2 ≠ (0, 0), then χ( ) = 0 or equivalently
) = 0 or equivalently

Solving this equation for  , we obtain two solutions:
, we obtain two solutions:

 - is always positive and
- is always positive and  + is positive if and only if 1 – η1 – η2 > 0. For
+ is positive if and only if 1 – η1 – η2 > 0. For  =
=  ± system (9) is equivalent to
± system (9) is equivalent to

or equivalently

Either 1 – η1 – η2 < 0, in which case  + is negative, or 1 – η1 – η2 > 0, in which case
+ is negative, or 1 – η1 – η2 > 0, in which case

This, together with (12), implies that (( -
- 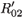 )2
)2 
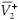 < 0). In either case we obtain an unphysical steady state. If
< 0). In either case we obtain an unphysical steady state. If  =
=  -, we have
-, we have

We distinguish two cases, 
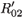 and
and  =
= 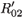 .
.
II.I. If 
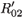 , then
, then

We claim that if R0 > 1 then 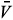 1 and
1 and 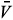 2 are positive. For this, we show that
2 are positive. For this, we show that

In fact, we have

A straightforward calculation shows that

If  <
< 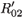 , then
, then

This implies that  < R0<
< R0< 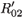 . Similarly, we show that
. Similarly, we show that 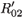 < R0<
< R0<  if
if 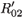 <
<  .Therefore, condition (14) is satisfied and consequently
.Therefore, condition (14) is satisfied and consequently 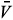 1,
1, 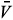 2 are positive if R0 > 1.
2 are positive if R0 > 1.
II.2. If  =
= 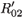 , then, R0 =
, then, R0 =  =
= 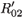 . In this case system (9) is equivalent, for
. In this case system (9) is equivalent, for  =
=  -, to
-, to

This implies that 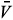 1 =
1 =  and =
and = 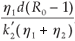 .
.
Proof of (7), the condition for a switch between strains: If  <
< 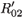 , then R01< R0 <
, then R01< R0 < 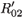 . Therefore,
. Therefore, 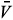 1- <
1- < 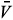 2- if and only if
2- if and only if
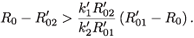
That is,

or equivalently

Taking the square of both sides and simplifying, we obtain

Then

This implies that
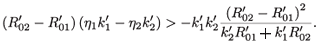
Since  –
– 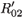 > 0, then
> 0, then

This is equivalent to 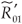 <
<  . Similarly, we show that if
. Similarly, we show that if 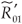 >
>  , then
, then 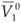 <
<  if and only if
if and only if 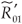 <
<  .
.
In the same manner as above we obtain that 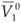 <
<  if and only if
if and only if 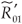 <
<  , where
, where 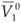 and
and  denote the values of V1 and V2 at the equilibrium before initiation of RTI. With this, condition (7) becomes a straightforward formulation of the switch condition in terms of the basic reproductive numbers.
denote the values of V1 and V2 at the equilibrium before initiation of RTI. With this, condition (7) becomes a straightforward formulation of the switch condition in terms of the basic reproductive numbers.
Proof that the virus-free steady state of system (2) is unstable when R0 > 1: System (2) is a non-autonomous system. We transform it into an autonomous system by setting ui,j(t) = cos (jω, s) and vi,j (t), for j = 1, , n, and adding the auxiliary equations satisfied by (ui,j, vi,j). We obtain
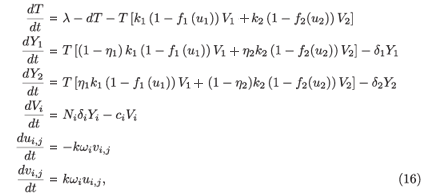
where i = 1, 2 and j = 1 n; and
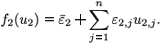
and
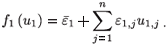
System (16) has two steady states, which correspond to the steady states of the averaged system of (2). Using the method described in Watmough and van den Driessche,16 we calculate the basic reproductive number,  0, which is exactly the basic reproductive number, (3), of the averaged system of (2) [calculated for εi (t) =
0, which is exactly the basic reproductive number, (3), of the averaged system of (2) [calculated for εi (t) =  , the mean value of εi (t)].
, the mean value of εi (t)].














