Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.5-6 Pretoria May./Jun. 2008
BIOLOGICAL MODELLING
Relating incidence to 'recent infection' prevalence: application to HIV
Alex Welte
DST/NRF Centre of Excellence in Epidemiological Modelling and Analysis (SACEMA), Stellenbosch University; and School of Computational and Applied Mathematics, University of the Witwatersrand, Private Bag 3, WITS 2050, South Africa. E-mail: alex.welte@wits.ac.za
ABSTRACT
I present a systematic approach to the derivation of relationships between disease incidence and the prevalence of an experimentally defined state of 'recent infection'. These depend, in general, on details of the population dynamic and epidemiological history, as well as the physiology of early disease progression. The general relations facilitate the evaluation of numerous approximate schemes that could be used for the purpose of estimating incidence from snapshot surveys. Methods for calibrating an incidence/prevalence relation from follow-up studies, for use in subsequent snapshot surveys, are considered. Example data from an ongoing follow-up study are analysed. Statistical power and prospects for practical implementation in southern Africa are also considered.
Introduction
Reliable estimation of disease incidence (rate of occurrence of new infections, as opposed to prevalence, which is the fraction of a population in an infected state at a particular time) is central to the determination of epidemiological trends, especially for the allocation of resources and evaluation of interventions. It is also important to have a rough measure of incidence in a population for the proper planning of sample sizes and costs for clinical trials and other population-based studies. Repeated follow-up of a representative cohort is the gold standard for estimating incidence, but is costly and time intensive, and is still prone to intrinsic problems such as the potential for a bias in the factors determining which subjects are lost to follow-up. Also, ethical considerations demand that a cohort study involve substantial support for subjects to avoid becoming infected, which may make the cohort unrepresentative of the population of interest.
Numerous methods have been proposed for inferring incidence from single or multiple cross-sectional surveys rather than following up a cohort.1–9 A central idea in some of these is to count the prevalence of some category of 'recent infection' which depends essentially on the recent incidence. The relationship between the two is in general not simple, and depends in detail on the recent population dynamics as well as distributions which capture the inter-subject variability of progression through stages of infection, as they are observed by the specific laboratory assays used. For this kind of approach to be sensible, a working definition of 'recent infection' must be calibrated, for example by repeatedly following up subjects over a period during which they become infected. This is effectively as much effort as one measurement of incidence by follow-up, after which the calibration could in principle be used to infer incidence from each of many subsequent independent cross-sectional surveys. Previous work on the inference of incidence from 'recent infection' prevalence has relied on a variety of assumptions and approximations, both in the modelling of the relationship between incidence and prevalence, and the calibration of the definition of 'recent infection'.
The present approach starts by expressing the relevant relationships with substantial generality. Special cases can then be considered, which allow the rearrangement of the relationships to facilitate the inference of incidence from survey data. This is done in the section immediately following this introduction. The section after that presents analysis of data from an acute infection cohort currently managed by the Centre for the AIDS Programme of Research in South Africa (CAPRISA). A model independent (distribution shape independent) estimation of the mean duration of a well-defined state of 'recent infection' can be performed on follow-up data of the kind obtained here. The statistical power of this data set, given the applicable definition of 'recently infected', is found to be very limited. Finally, I evaluate the prospects for developing efficient methods of estimating incidence from surveys of the prevalence of 'recent infection' in southern Africa, in light of currently available data.
Relating 'recent infection' prevalence to incidence
I now outline a quite general approach to relating the key demographic, epidemiological and biological processes that are relevant to indirect estimation of incidence from single surveys of the prevalence of 'recent infection'. Let a population be characterized by a gross incidence I, and corresponding per person incidence, i. This means that in a period dt, around time t, the number of new cases is I(t) dt = i(t)Ns(t) dt, where Ns is the susceptible population. If observed through the application of two separate laboratory assays of different sensitivity, infected individuals experience the following key events:
1. The moment of infection itself, at some time t0.
2. Entry into the 'recently infected' category (infection now detectable only by assay one). This occurs at the individual's own delay of t1 after infection.
3. Exit from the 'recently infected' category (infection now also detectable by assay two). This happens at the individual's own delay of t2 after infection.
4. Death, from whatever cause, at a delay of t3 after infection.
Henceforth, whenever the term 'recent infection' is used, it will mean infection being detectable by only the first of two assays. The duration of this kind of state is sometimes referred to as a 'window period', and we will also refer to entry and exit from the 'window state'. The distribution of waiting times t1, t2 and t3 over the population is given by some distribution ρ(t1, t2, t3), which captures the full range of biological variation in mortality and disease progression as probed by the relevant assays. It is in principle conceivable that for some individuals t1 > t2, so that they never appear to be recently infected. Even when t1 < t2 there is the possible complication that t3 < t1 or t1 < t3 < t2, i.e. that the subject dies before entering or leaving the state of recent infection. In such a case the values of either t1 or t2 should be taken as effectively infinite or undefined. This means that the total density of the distribution ρ(t1, t2, t3) might be less than unity when integrated over any finite range of the t's. These are very minor points for many situations, such as the definition of recent infection induced by the data presented in the next section.
We can now write down expressions for the expected number of persons in various categories at the time of observation, tobs, i.e. the counts of recently infected persons (Nr), long-infected persons (Nl) and non-infected persons (Nn), as categorized by the use of two assays of different sensitivity. Note that Nr also counts people too recently infected to be detectable by any assay being used. For convenience, we will set tobs = 0. The total number of persons historically infected is now given by
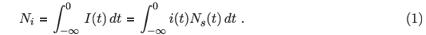
In a continuous formulation of population dynamics, we can consider an infinitesimal cohort of infected individuals created in a period dt. If we are interested in events preceding the measurement at tobs = 0, we will consider individuals infected at some time t < 0. In the infinitesimal cohort of individuals infected around time t < 0, the probability of any member being alive and classified as recently infected at tobs = 0 is given by

The approximation that we replace ρ(t1, t2, t3) with ρ(t1, t2) amounts to assuming that the state of recent infection typically lasts for a short time compared to the survival time after infection. The expected number of persons classified as recently infected is then
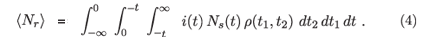
The analogous expression for the expected number of people who are classified as infected but not recently infected, i.e. long infected, is then
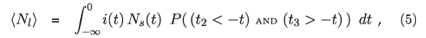
which does not admit the elimination of t3.
A further simplification, which is worth noting, is the possibility of disregarding the delay between infection and detectability of infection by the more sensitive assay. For any sensible assay this time is likely to be short compared to any natural timescale of substantial population dynamic shifts, so it does not matter much whether we are measuring the rate at which people become infected or the rate at which people are becoming detectably infected. Then we can set
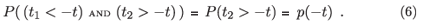
If we need to consider expressions containing explicit survival schedules, such as P ((t1 < –t) AND (t2 > –t) AND (t3 > –t)), then the simplest sensible approximation is that there is a 'post infection' mortality µI that is approximately constant over times relevant to the survey. In this case P ((t1 < –t) AND (t2 > –t) AND (t3 > –t)) can be replaced by p(-t)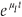 .
.
The time dependence of i and Ns can in principle be complicated, but can instructively be decomposed into a constant and time varying piece:

When Δi/i and ΔNs/Ns are suitably small, over times comparable to the average duration of the recently infected state, we can regard i and Ns as approximately constant.
The intended use of the relationship between incidence and the prevalence of recent infection is for inferring incidence. We divide inputs into this process into three types, which reflect the way the method is likely to be used:
-
Calibration data: inputs obtained from previous longitudinal surveys, which capture aspects of the correlation between physiology and assays—i.e. information about ρ(t1, t2, t3).
-
Demographic data: input which summarizes our knowledge or assumptions about the underlying population dynamic—i.e. the history of the population of susceptibles Ns.
-
Snapshot survey data: the data gathered for each instance of an incidence measurement—i.e. a count of the number of recently infected (Nr), non-infected (Nn) and long-infected (Nl) individuals in a sample of the population in which incidence is to be estimated.
In general, it is not possible to obtain expressions for i(0) in terms of knowable inputs. We will now consider special cases where i(0) can be inferred.
When i and Ns can be regarded as approximately constant as per (7) and (8), we can write

where
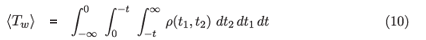
is just the mean window period (see derivation below) and we can use the observed Nn as an approximation for Ns. In practice, the uncertainties induced by imperfect calibration (estimation of 〈Tw〉) and the counting error in the sample of persons surveyed will dominate the minor discrepancy introduced by Nn ≈ Ns .
We now demonstrate that the expression 〈Tw〉 in (10) is in fact just the mean window period as defined by two assays of different sensitivity. This is an important point because it means that a calibration need not determine the shape of the distribution ρ({ti}) in any detail, as long as the mean is estimated. The simplest case would be obtained if all persons experience identical disease progression, i.e. everyone experiences the same delays, from infection, to entry and exit from the recent infection state, namely T1 and T2, respectively, so that

where by δ we mean the Dirac delta function. In this case
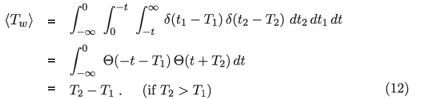
where Θ is the step function with the property that Θ(x) = 1 if x > 0 and 0 otherwise. If there is genuine inter-subject variability, we can write ρ(t1, t2) as a superposition of delta functions:
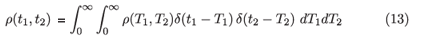
and then change the order of integration to get
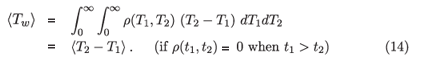
Note that while the unbiased population level mean of the window period is used to convert between recent infection prevalence and incidence, an actual sample of subjects in the window period obtained by a cross-sectional survey will be biased towards subjects with longer window periods. Some suitably unbiased follow-up study would be required to estimate the mean window period 〈Tw〉.
The extraction of an expression of the current incidence in terms of knowable variables is less simple when we do not assume i(t) and Ns(t) to be constants over the times sampled by the applicable ρ and survival schedule. We do not pursue this in any more detail at this time because we do not have credible calibration data available in this regime.
Calibration of 'window period' duration
We now investigate the prospects for calibrating the simple expression in Equation (9), which, we recall, is applicable when: 1) the window period duration is distributed over times which are small compared with the time on which population dynamics produces substantial effects, and 2) mortality is insignificant.
This is the case, for example, when the two assays are 1) testing for viral RNA positivity/negativity (RNA±), and 2) testing for antibody positivity/negativity (AB±).
An example of a study which in principle facilitates a calibration is a repeat follow up of initially uninfected subjects, using both assays at each visit. This is currently implemented in an 'acute infection cohort' (AIC) managed by CAPRISA. A data update obtained in January 2007 indicated a directly observed incidence of 6% (21 infections detected in 348 person years of follow up).
We assume that the moment of infection, and hence the moment of crossing the RNA positivity threshold, is totally uncorrelated with the follow-up visit schedule, which is presumably the case, and which means that the times at which subjects become RNA positive are uniformly distributed within the intervals in which they can be located by follow up. Then the probability that a subject who crosses the RNA threshold between two observations, at times –Δ and 0, will fail to cross the antibody threshold by time 0, is
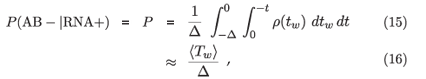
where ρ(tw) is the distribution of window periods ρ(t2 – t1) induced by some underlying ρ(t1, t2). The last step (obtained from integration by parts) is exact if the cumulative density of the window period distribution, c(t) =  ρ(tw) dtw, obeys
ρ(tw) dtw, obeys

which is approximately true in the CAPRISA AIC. Here we have Δ ≈ 30 days, and the sensitivity of the (ELISA) antibody test used in this study, as found a posteriori in the calibration we are about to perform, is such that there is little to no chance of having a window period in excess of Δ. This means that we can directly estimate the value 〈Tw〉 of from the follow-up data without knowing anything about the structure of ρ(t1, t2).
The inference for 〈Tw〉 then proceeds by counting the fraction of infected subjects who were seen in the RNA+/AB– state. The likelihood of observing a given number Nr in this window, of a total n who became infected, is binomially distributed, where the probability of any one being seen in this state is P in (15).
The data from the CAPRISA AIC study gives Nr = 4, n = 19 and 〈Δ〉 = 29 days, which leads to a likelihood as a function of 〈Tw〉 indicated in Fig. 1 (solid line). Note that two of the subjects who became infected and were included in the incidence calculation mentioned above were excluded from this analysis due to missing data that made it impossible to pin down a precise interval between 'last RNA–' and 'first RNA+ with known antibody result'. Using the specific inter-visit intervals for each subject:
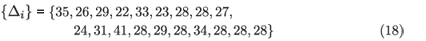
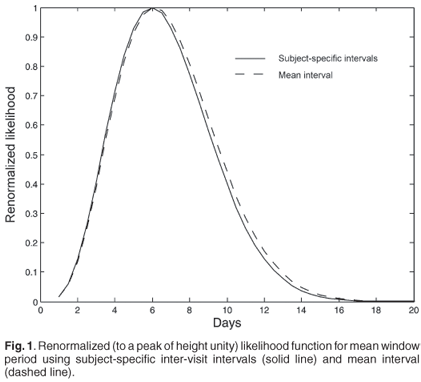
instead of their mean, requires enumerating all possible choices of which subjects were found in the RNA+/AB– state, and explicitly adding the probabilities of all possible ways of finding 4 of 19 newly infected subjects in the window period. This produces the dashed line likelihood function in Fig. 1. The difference between the two curves is not significant. The uncertainty in the calibration parameter 〈Tw〉 that results is in any case too broad for a viable inference of incidence to be made with such a calibration. The problem is essentially that the window period state is so transient that it is seldom observed, and it would require an unrealistically large cohort to produce a good inference, either for calibration purposes or for estimating incidence. With this calibration, the uncertainty seen in Fig. 1 is the minimum uncertainty in any inference, even if the sample were so large as to produce neglible counting error.
As a simple consistency check, we can generate an 'effective' value of Nr/Ns = 4/4462 = 0.0009 by considering all visits in the study as being part of a large survey. Together with the maximum likelihood value for 〈Tw〉 = 0.019 years, this yields a maximum likelihood value for incidence of 5.5% per annum. This is consistent with the directly observed value of 6%, noting that the two data sets required slightly different censoring, and the maximum likelihood result is from a very broad likelihood distribution which is not near a normal distribution limit.
The CAPRISA AIC study is designed to gather substantial information on subjects over the course of five years post infection, most particularly in the early phase. A preliminary investigation has been done to assess the possibility of extracting mean trends in growth of viral loads. This was intended as a possible way of adjusting inferred values of 〈Tw〉 if a viral load assay of known different sensitivity were to be used instead of the one used in this study. This appears not to be a viable way of adjusting the window period, because the window period is too short for practical purposes (and hence one should really extend it by stretching typical values of t2). There appears not to be any quantitative theory about the growth in the strength of antibody response relevant to the assay used.
Summary and prospects for further work
For the foreseeable future, it will be of the utmost importance to evaluate the state of the HIV epidemic, and other serious diseases. It is expensive, time-consuming and difficult to obtain good direct estimates of disease incidence by following large cohorts, so indirect methods must be developed. These inevitably require some assumptions and calibrations to be made, in order that the indirect data, such as a snapshot of recent infection prevalence, can be systematically used in an inference of incidence.
I have presented a general framework, in which a variety of special cases can be considered, for relating the current state of an epidemic to its recent history, and hence inferring incidence from prevalence type measures. For this approach to yield a satisfactory amount of statistical power, it is required that a state of recent infection be observed suitably often to yield acceptable counting error, which affects both the calibration and subsequent cross-sectional surveys. Note that the conversion between a survey-measured prevalence and the recent disease incidence inherits the uncertainties of the calibration. The use of the RNA+/AB– state as a definition of recent infection appears impractical under the conditions considered in the sample data presented. Perhaps a less sensitive version of the antibody test would extend the window period and make recent infection easier to catch in a survey, but it would also mean that a brand new calibration on a large cohort would be required.
What would be useful then, is a definition of recent infection which
1) can be reliably calibrated from readily available follow-up data, and
2) has a long enough mean duration to be observed with reasonable counting errors in modestly sized samples.
In terms of these criteria, probably the strongest candidate in the southern African context appears to be the definition of recent infection available by the use of the 'BED assay', which has been proposed in other populations (see, for example, refs 4, 5, 8). This is done by defining recent infection as obtaining an optical density (the ultimate result of the BED assay measurement) which is above the background noise, but below an arbitrary threshold. It is possible to choose this threshold to obtain median window periods of around 200 days, which addresses the sample-size problem just noted. There are several major studies in the region in which the BED assay has been widely used, and the assay is reliable when applied to stored dry blood spots, so it can be used in a subsidiary analysis to other studies if ethical clearance can be obtained. What makes this suggestion controversial is that the distribution of the window period has an essentially infinite tail, meaning that some subjects, if assessed solely by the BED assay, are classified as recently infected for all times. This complicates the calibration of any proposed incidence inference, and the choice of approximations to the general dynamics expressed in (4). Developing the required method, within the framework outlined here, and in light of the specific structure of the regionally available BED follow-up data and other known population dynamic parameters, is the subject of ongoing work.
I wish to thank the CAPRISA 002: Acute Infection study for providing data for this analysis. CAPRISA is part of the Comprehensive International Program of Research on AIDS (CIPRA) and is supported by the National Institute of Allergy and Infectious Disease (NIAID), the National Institutes of Health (NIH) and the US Department of Health and Human Services (DHHS) (grant AI51794). Lise Werner and Anneke Grobler facilitated this project by extracting and documenting data from the AIC database. Tom McWalter provided substantial critical comments on the manuscript, and a reviewer's comments helped improve the clarity of the exposition around waiting times.
1. Brookmeyer R. and Quinn T.C. (1995). Estimation of current human immunodeficiency virus incidence rates from a cross-sectional survey using early diagnostic tests. Am. J. Epidemiol. 141(2), 166–172. [ Links ]
2. Posner S.J. et al. (2004). Estimating HIV incidence and detection rates from surveillance data. Epidemiology 15, 164–172. [ Links ]
3. Jannssen R.S. et al. (1998). New testing strategy to detect early HIV-1 infection for use in incidence estimates and for clinical and prevention purposes. JAMA 280(1), 42–48. [ Links ]
4. Parekh B.S. et al. (2002). Quantitative detection of increasing HIV type 1 antibodies after seroconversion: A simple assay for detecting recent HIV infection and estimating incidence. AIDS Research and Human Retroviruses 18(4), 295–307. [ Links ]
5. Parekh B.S. and McDougal J.S. (2001). New approaches for detecting recent HIV-1 infection. AIDS Rev. 3, 183–193. [ Links ]
6. Cole S.R., Chu H. and Brookmeyer R. (2006). Confidence intervals for biomarker-based human immunodeficiency virus incidence estimates and differences using prevalent data. Am. J. Epidemiol. 165(1), 94–100. [ Links ]
7. Nascimento C.M.R. et al. (2004). Quantitative detection of increasing HIV type 1 antibodies after seroconversion: a simple assay for detecting recent HIV infection and estimating incidence. AIDS Research and Human Retroviruses 20(11), 1145–1147. [ Links ]
8. McDougal J.S. et al. (2006). Comparison of HIV type 1 incidence observed during longitudinal follow-up with incidence estimated by cross-sectional analysis using the BED capture enzyme immunoassay. AIDS Research and Human Retroviruses 22(10), 945–952. [ Links ]
9. Wong K., Tsai W. and Kuhn L. (2006). Estimating HIV hazard rates from cross-sectional HIV prevalence data. Statistics in Medicine 25(11), 2441–2449. [ Links ]














