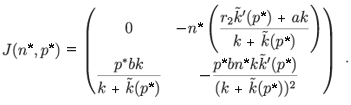Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.5-6 Pretoria May./Jun. 2008
BIOLOGICAL MODELLING
Predator density-dependent prey dispersal in a patchy environment with a refuge for the prey
K. Dao DucI, *; P. AugerI, II; T. Nguyen-HuuI, II
IIXXI, ENS Lyon,46 allée d'Italie, 69364 Lyon cedex 07, France
IIIRD UR Geodes, Centre IRD de l'Ile de France, 32, Av. Henri Varagnat, 93143 Bondy cedex, France
ABSTRACT
In this article, we examine a two-patch predator–prey model which incorporates a refuge for the prey. We suppose that prey migration is dependent on predator density, according to a general function. We consider two different time scales in the dynamics of the model, a fast one describing patch to patch migration, and a slow one involving local prey and predator interaction. We take advantage of the time scales to reduce the dimension of the model by use of methods of aggregation of variables, and thereby examine the effect of predator density-dependent migration of prey on the stability of the predator–prey system. We establish a simple criterion of viability, namely, the existence of a positive and globally stable equilibrium, and show that density dependence has beneficial effects on both species by providing larger equilibrium densities.
Introduction
Predator–prey theory has long been and remains a dominant and important theme in ecology and mathematical ecology, for which many problems remain open.1 Considered since the first Lotka-Volterra model as a classical application of mathematics in biology, models based on differential equations for interactions between species, thanks to analytical techniques and computerization, have become progressively more complex. They increasingly give a more realistic description of ecological systems, and thereby have improved our understanding of the dynamic relationship between prey and predator. The hiding behaviour of prey in particular has been incorporated as an important ingredient of predator–prey systems2 and its consequences on stability have been studied in several models. The traditional way in which refuge has been introduced is via a 'snapshot' approach, requiring that a constant proportion or number of prey cannot be killed by the predators.3 Some early theoretical work suggests that the use of refuges by prey, according to this approach, has a stabilizing effect on predator–prey dynamics,4–6 whereas other models show no such simple pattern.7,8
More recently, several studies have taken into account the dynamic nature of the refuge, and more generally, the importance of spatial heterogeneity,9,10 using patchy environment in their models.11–13 The behavioural aspect of this kind of migration focuses on its possible modalities. The density dependence of dispersal has been studied in many papers, whereas the dependence of predator density in prey migration13,14 is relatively less studied than the dependence of prey density in predator migration.15–18 Spatial heterogeneity leads to the consideration of two different types of dynamics – local interactions between species, on the one hand, and migrations from patch to patch on the other. In some cases, there exist two different time scales (for instance, a fast time scale corresponding to individual processes like migration, and a slow one for demographic changes (see ref. 14); it is then possible to reduce, via results provided by geometrical singular perturbation (GSP) theory, the dimension of the mathematical model to obtain a reduced or 'aggregated' model which can be handled analytically).19–21 It has been shown11 by using these methods that the refuge has a stabilizing effect on the equilibrium for a simple Lotka-Volterra model with refuge and density-independent migration. The purpose of this article is to examine the impact of predator density on the migration of prey in such a model. We add here the idea that, to survive, prey has to search for resources outside its refuge and so exposes itself to predation.
We first describe the predator–prey model, comprising a set of three ordinary differential equations governing the local dynamics of prey and predator population densities. These dynamics present two time scales, which enables us to use aggregation of variables methods, based on perturbation techniques and on application of a centre manifold theorem of Fenichel26 to reduce the model to an aggregated one that consists of two equations. To evaluate the impact of density dependence in general, our model also uses a general predator density-dependent function for prey migration. We then study this model and its equilibrium points, and find a simple criterion of stability for a positive equilibrium, depending on various parameters and on the density-dependent migration function. The stability analysis of the non-trivial equilibrium point so found is then considered with a discussion of the results and their ecological interpretations.
The predator–prey model
The model considers two patches, 1 and 2. The prey can move on both patches whereas the predator remains on patch 1. Patch 2, therefore, is a refuge for the prey. Let us denote ni(t) as the density of the prey at time t on patch i (i = 1, 2) and p(t) the density of the predator at time t on patch 1.
We assume that there are two different time scales of the associated dynamics. Migrations are considered to be fast compared to predator–prey interactions. In the prey equations, the dynamics on patch 1 (conversely 2) is represented by a positive (conversely negative) term describing the natural growth (conversely mortality, as there are no resources in the refuge) and a negative term representing prey killed by predators on patch 1. For the predator, we consider a constant natural mortality rate and assume that growth is proportional to the density of prey captured.
The complete system, composed of a set of three ordinary differential equations, is described as follows:
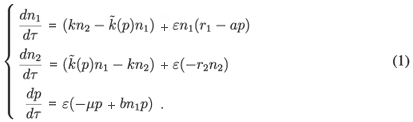
The term r1 > 0 represents the intrinsic growth rate of the prey population in patch 1. Terms r2 and µ are natural mortality rate for prey in patch 2 and for predator in patch 1, respectively. The predation rates are given by a and b. The parameter k represents the prey migration rate from patch 2 to patch 1; the prey migration rate from patch 1 to patch 2 is assumed to be predator-density dependent with the function 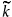 (p), which we suppose to be positive and to increase with p. In other words, the more predators found on a patch, the more prey tends to leave the patch. We suppose
(p), which we suppose to be positive and to increase with p. In other words, the more predators found on a patch, the more prey tends to leave the patch. We suppose 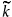 (0) > 0 because there is a natural migration from the resource patch to the refuge even if there is no predator.
(0) > 0 because there is a natural migration from the resource patch to the refuge even if there is no predator.
Let us define:
n(t) = n1 + n2 (t),
which is the total prey density. Our reduction method is based on classical aggregation methods.21 We now consider the model as an ε-perturbation of the non-perturbed problem obtained for ε = 0, which presents the following fast equilibrium:

with
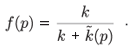
For each value of n and p, this equilibrium is hyperbolically stable, which means that this set of fast equilibria constitutes an attracting two-dimensional invariant set for small positive values of ε. With this result, the centre manifold theorem given using Fenichel26 allows us to approximate by a Taylor expansion with respect to the small parameter ε the restriction of the complete model to this invariant set. The first-order expansion gives the aggregated model. If this model is structurally stable, then the complete model is topologically equivalent to the reduced model and we obtain a good idea of the behaviour of the complete model by using the aggregated model (see also refs 25, 27 and 28, which give a detailed description of the theorem with many applications). To derive the reduced model, we substitute the fast equilibria with n1 and n2 and we add the first two equations, giving the following system (with the slow time scale t = ετ):
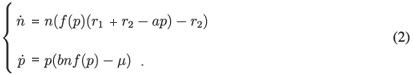
The aggregated model
Let us now study the aggregated model given by (2). First, we determine the nullclines of the system:
• The n-nullclines are given by
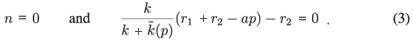
• The p-nullclines are given by
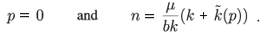
As the equilibrium points of the model are the intersections between the p-nullclines and the n-nullclines, we see that there exists a non-trivial equilibrium in 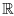 +2 if Equation (3) admits a positive solution. A necessary and sufficient condition in this case is kr1 -
+2 if Equation (3) admits a positive solution. A necessary and sufficient condition in this case is kr1 - 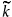 (0) r2 > (see Appendix A). Let us define a new parameter λ as follows: λ = kr1 -
(0) r2 > (see Appendix A). Let us define a new parameter λ as follows: λ = kr1 - 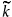 (0) r2. The sign of λ then determines the behaviour of the system.
(0) r2. The sign of λ then determines the behaviour of the system.
• If λ < 0, we have only (0, 0) as an equilibrium point, whose associated Jacobian matrix is
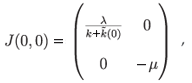
which leads to the conclusion that it is a stable node (Tr(J) < 0 and Det(J) > 0).
• If λ = 0, the n-axis constitutes a set of equilibrium points which are not isolated. In this case, the ε-error can play an important role in the dynamics (see ref. 11, for example). Indeed, as shown in this previous paper, the approximation does not match the complete model. Consequently, we have to obtain a first-order approximation of the manifold. In Appendix B, we perform this approximation and give some analytical results for the new model, providing a good example of a case where a more precise approximation of the manifold is necessary.
If λ > 0, we have two equilibrium points:
– (0, 0), which is a saddle point (DetJ(0, 0) < 0)
– (n*, p*), whose Jacobian matrix associated with (n*, p*) is (see Appendix C)
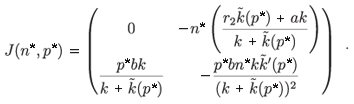
The trace of this matrix is strictly negative and the determinant is positive. Consequently, (n*, p*) is a locally stable equilibrium point. Figures 1 and 2 illustrate the two cases λ < 0 and λ > 0 with the function 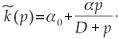
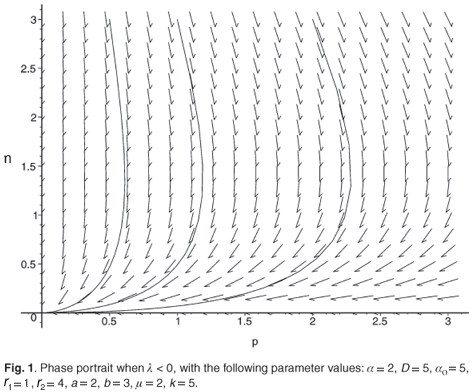
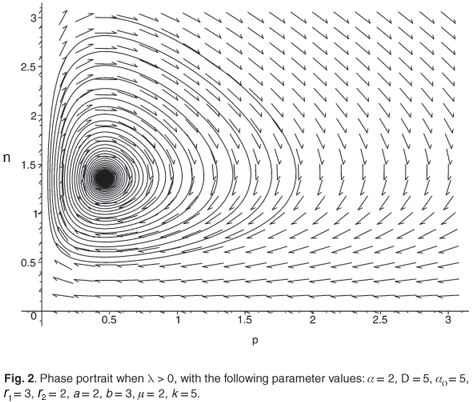
We see that the system is viable (i.e. it does not lead to extinction) if and only if the parameter λ is positive. In this case, we have an equilibrium point, whose global asymptotic stability is the subject of the next section.
Global asymptotic stability of (n*, p*)
To prove that (n*, p*) is globally asymptotically stable, we first show that any orbit starting in 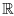 +2 is bounded; in other words, that there exists a compact in which this orbit stays closed.
+2 is bounded; in other words, that there exists a compact in which this orbit stays closed.
From the study of the nullclines of the system, we proved that every orbit starting in 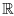 +2 stays in
+2 stays in 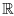 +2. Moreover, we know the form of the orbits
+2. Moreover, we know the form of the orbits 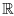 +2; they circle the equilibrium point (n*, p*). We can therefore define a return map (called first map of Poincaré) for this vector field (see Fig. 3).
+2; they circle the equilibrium point (n*, p*). We can therefore define a return map (called first map of Poincaré) for this vector field (see Fig. 3).
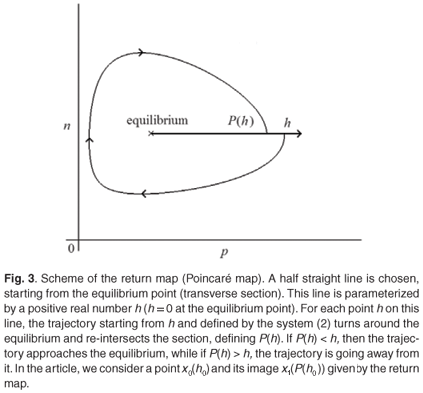
We now consider the horizontal transverse section S starting from the equilibrium point (see Fig. 3; we verify that the field is never horizontal on S and a point x0(h0), whose trajectory is denoted by γ(x0). We now show that P(h0) – h0 < 0. Let us consider x1(P(h0)) and the closed curve Γ consisting of the segment [x0, x 1] and the part of the orbit joining x0 and x1. Let us note the vector field 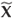 defined by
defined by
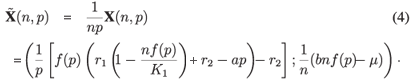
Using the Stockes theorem in the domain D delimited by Γ, we have:

As 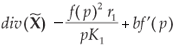 < 0 on D, by definition of the curve Γ, the right-hand part of Equation (5) is reduced to an integral along the transverse section. The sign of that expression is that of P(h0)–h0, which gives the result. We have therefore shown that the trajectory always progresses towards the inside and so is included in a compact (delimited by Γ). In such a compact, we now show that the trajectory can converge only to the equilibrium point. Using the Poincaré-Bendixson theorem (which describes precisely all possible kinds of trajectories of a plane dynamical system – see refs 22 and 23 for details and demonstration), and because the compact considered contains only one singular point, there can be only two kinds of behaviour:
< 0 on D, by definition of the curve Γ, the right-hand part of Equation (5) is reduced to an integral along the transverse section. The sign of that expression is that of P(h0)–h0, which gives the result. We have therefore shown that the trajectory always progresses towards the inside and so is included in a compact (delimited by Γ). In such a compact, we now show that the trajectory can converge only to the equilibrium point. Using the Poincaré-Bendixson theorem (which describes precisely all possible kinds of trajectories of a plane dynamical system – see refs 22 and 23 for details and demonstration), and because the compact considered contains only one singular point, there can be only two kinds of behaviour:
• The ω-limit set ω(x0) (which is the set of accumulation points of the trajectory) is a single point
, which is an equilibrium point; the flow of the differential equation Φ(t, x0) tends towards
as t → ∞
• ω is a periodic orbit.
Moreover, we have shown previously that as div(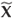 ) < 0, there cannot be any periodic orbit (this result is known as the Dulac criterion (see ref. 29), which gives a criterion of non-existence of periodic orbit for a plane dynamical system). Consequently, ω(x0) is reduced to a single point and we reach the conclusion: (n*, p*) is globally asymptotically stable.
) < 0, there cannot be any periodic orbit (this result is known as the Dulac criterion (see ref. 29), which gives a criterion of non-existence of periodic orbit for a plane dynamical system). Consequently, ω(x0) is reduced to a single point and we reach the conclusion: (n*, p*) is globally asymptotically stable.
Discussion and conclusion
We have shown that for ε < 1, we were able to reduce the 3-dimension initial system to a 2-dimension aggregated model which presents two general behaviours, depending on the sign of the parameter λ:
If λ < 0, then the system is not viable. (0, 0) is globally asymptotically stable. The same result applies for λ = 0, because the predators are then extinct.
If λ > 0, there is a non-trivial globally asymptotically stable point.
This result can easily be interpreted: the sign of λ depends on the quotient of two quantities k/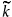 (0) and r1/r2, the first denoting the quotient between the migration terms when there are predators, and the second the quotient between the terms of global growth. When there are no predators, if the migration from patch 1 to patch 2 is too important, the prey population naturally disappears as patch 2 is hostile. Note that the influence of
(0) and r1/r2, the first denoting the quotient between the migration terms when there are predators, and the second the quotient between the terms of global growth. When there are no predators, if the migration from patch 1 to patch 2 is too important, the prey population naturally disappears as patch 2 is hostile. Note that the influence of 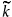 on the qualitative behaviour of the system is determined only by its value for p = 0. This result shows that the degree of predator-density dependence of prey dispersal has no influence on stability, whereas in ref. 17, prey-density dependence of predator dispersal could destabilize as the degree of density dependence increases.
on the qualitative behaviour of the system is determined only by its value for p = 0. This result shows that the degree of predator-density dependence of prey dispersal has no influence on stability, whereas in ref. 17, prey-density dependence of predator dispersal could destabilize as the degree of density dependence increases.
We now want to compare the case of density-independent migrations with the case of density-dependent migrations. The density-independent case was studied in a previous paper.11 In this article, we obtained a similar result of global stability of a unique positive equilibrium for the aggregated model. Now, let us focus on prey and predator equilibrium densities.
We return to the predator-density-dependent migration rate of prey. A particular function is the following:
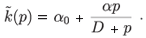
In a more general way, we can write this as follows:
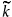 (p) = α0 + h(p)
(p) = α0 + h(p)
where h(p) is a strictly positive and increasing function for any p > 0 with h(0) = 0. The density-dependent migration rate is then the sum of two terms, a constant term α0 and the density-dependent term h(p). Therefore, we can consider two cases, the density-independent case where 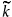 (p) = α0, and the density-dependent case where
(p) = α0, and the density-dependent case where 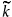 (p) = α0 + h(p)
(p) = α0 + h(p)
In both cases, the positive equilibrium (n*, p*) is given by the following expressions:
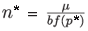
and
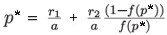
where f(p*) represents the prey proportion on patch 1 at the fast equilibrium for the positive equilibrium (n*, p*) of the aggregated model.
Let us denote respectively 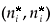 and
and 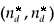 the equilibrium in the density-independent and the density-dependent cases.
the equilibrium in the density-independent and the density-dependent cases.
In the density-independent case, the equilibrium prey and predator densities are the following:

In the density-dependent case, the equilibrium densities become
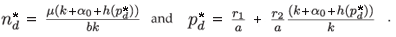
This can be written:
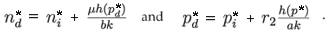
Remember that the function h(0) = 0 and h is a monotonous increasing function of p. Therefore, equilibrium densities for prey as well as for predator are larger in the density-dependent case than in the density-independent case (Fig. 4).
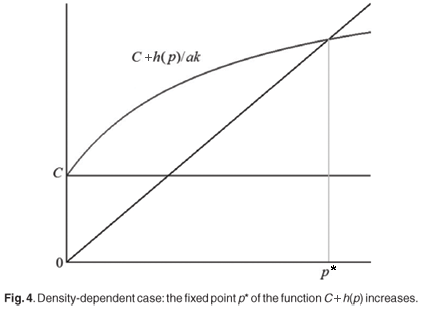
As a consequence, we find that the predator-density dependence of prey migration has important consequences for the predator–prey community. It has a positive effect on both species by providing larger prey and predator densities at equilibrium. In a certain sense, we can conclude that it increases the fitness of the predator–prey community. Communities in which prey individuals move according to predator-density migration rules are more likely to spread with larger population densities at equilibrium. It is interesting to see that the mechanism not only increases the equilibrium density of prey but also that of predator. A priori, one could imagine that when prey is more efficient at avoiding predation, predators would have more difficulty capturing prey and this would lead to a decrease in predator density at equilibrium. However, our result shows that this is not the case and that the predator density-dependent mechanism for prey migration is not only beneficial for prey but also for predator. The density of prey available for predation is less, which cause a loss of predation efficiency, but the total prey density is greater. It appears that it is more profitable for the predator to exploit a large reservoir at a regulated rate, even with a loss of efficiency, than to create a situation in which prey cannot escape while too many predators are located on the capture patch, as might occur in the case of density-independent migration. The density-dependent migration of prey prevents an overcapture of prey by predators. Hence density-dependent migration regulates interactions between prey and predators better, leading to a higher population density for both species.
1. Berryman A.A. (1992). The origins and evolutions of predator–prey theory. Ecology 73, 1530–1535. [ Links ]
2. Berryman A.A. and Hawkins B.A. (2006). The refuge as an integrating concept in ecology and evolution. Oikos 115(1), 192–196. [ Links ]
3. Taylor R.J. (1984). In Predation, p. 166. Chapman and Hall, New York. [ Links ]
4. Holling C.S. (1959). Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398. [ Links ]
5. Sih A., Petranka J.W. and Kats L.B. (1998). The dynamics of prey refuge use: a model and tests with sunfish and salamander larvae. Am. Nat. 132(4), 463–483. [ Links ]
6. Kar T.K. (2005). Stability analysis of a prey–predator model incorporating a prey refuge. Communications in Nonlinear Science and Numerical Simulation 10(6), 681–691. [ Links ]
7. Gonzalez-Olivares E. and Ramos-Jilberto R. (2003). Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol. Model. 166(1-2), 135–146. [ Links ]
8. Collings J.B. (1995). Bifurcation and stability analysis of a temperature-dependent mite predator–prey model incorporating a prey refuge. Bill. Mayh. Biol. 57, 63–76. [ Links ]
9. Levin L.S. (1976). Population dynamics models in heterogeneous environments. Annu. Rev. Ecol. Syst. 7, 287–310. [ Links ]
10. Hanski I. (1981). Coexistence of competitors in patchy environments with and without predation. Oikos 37, 306–312. [ Links ]
11. Poggiale J.C. and Auger P. (2004). Impact of spatial heterogeneity on a predator–prey system dynamics. C.R. Biol. 327, 1058–1063. [ Links ]
12. Abrams P. (2007). Habitat choice in predator–prey systems: Spatial instability due to interacting adaptative movements. Am. Nat. 169, 581–597. [ Links ]
13. Mchich R., Bergam A. and RaVssi N. (2005). Effects of density dependent migrations on the dynamics of a predator preymodel. Acta Biotheor. 53(4), 331–340. [ Links ]
14. Mchich R., Auger P. and Poggiale J.C. (2007). Effect of predator density dependent dispersal of prey on stability of a predator–prey system. Math. Biosci. 206(2), 343–356. [ Links ]
15. Amarasekare P. (1998). Interactions between local dynamics and dispersal: Insights from single species models. Theor. Popul. Biol. 53, 44–59. [ Links ]
16. Amarasekare P. and Nisbet R.M. (2001). Spatial heterogeneity, source-sink dynamics, and the local coexistence of competing species. Am. Nat. 158(6), 572–584. [ Links ]
17. Murdoch W.W., Briggs C.J., Nisbet R.M., Gurney W.S.C. and Stewart-Oaten A. (1992). Aggregation and stability in metapopulation models. Am. Nat. 140, 41–58. [ Links ]
18. Mchich R., Auger P.M., Bravo de la Parra R. and Raissi N. (2002). Dynamics of a fishery on two fishing zones with fish stock dependent migrations: aggregation and control. Ecol. Model. 158, 51–62. [ Links ]
19. Auger P., Charles S., Viala M. and Poggiale J.C. (2000). Aggregation and emergence in ecological modelling: integration of the ecological levels. Ecol. Model. 127, 11–20. [ Links ]
20. Auger P., Chiorino G. and Poggiale J.C. (1998). Aggregation, emergence and immergence in hierarchically organized systems. Int. J. Gen. Syst. 27(4-5), 349–371. [ Links ]
21. Auger P. and Poggiale J.C. (1995). Emerging properties in population dynamics with different time scales. J. Biol. Syst. 3(2), 591–602. [ Links ]
22. Francoise J.P. (2000). Oscillations en biologie – Analyse qualitative et modeles – Mathematiques & Applications 46. Springer, Berlin. [ Links ]
23. Arrowsmith D.K. and Place C.M. (1992). In Dynamical Systems: Differential Equations, Maps and Chaotic Behavior. Chapman & Hall, London. [ Links ]
24. Auger P., Bravo de la Parra R., Poggiale J.C., Sanchez E. and Nguyen Huu T. (2007). Aggregation of variables and applications to population dynamics. Springer, Berlin. [ Links ]
25. Carr J. (1981). In Applications of Centre Manifold Theory. Springer-Verlag, New York. [ Links ]
26. Fenichel N. (1971). Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J. 21(3), 193–226. [ Links ]
27. Hirsch M.W., Pugh C.C. and Schub M. (1970). Invariant manifolds. Bull. Am. Nat. 153, 1015–1019. [ Links ]
28. Sakamoto K. (1990). Invariant manifolds in singular perturbations problems for ordinary differential equations. Proc. Roy. Soc. Edin. 116A, 45–78. [ Links ]
29. Hale J. and Kocak H. (1991). Dynamics and Bifurcations. Springer-Verlag, New York. [ Links ]
* Author for correspondence. E-mail: khanh.dao_duc@ens-lyon.fr
Given that the n-isocline 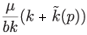 is always positive for p > 0, there exists a unique positive equilibrium point if and only if the equation
is always positive for p > 0, there exists a unique positive equilibrium point if and only if the equation
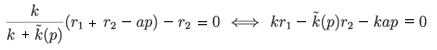
admits a positive root. Let us denote
F(p) = kr1 - 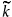 (p)r2 - kap.
(p)r2 - kap.
Since F(p) is decreasing and F(p) → –∞as p → ∞, there exists a positive root if and only if F(0) > 0. In other words, the parameter λ = kr1 - 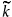 (0)r2 must be positive.
(0)r2 must be positive.
Let us rewrite the system (1) the following equivalent way:
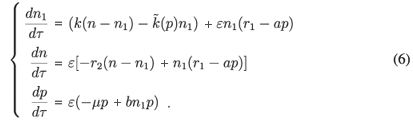
To get a first-order approximation of the manifold, the method consists in writing
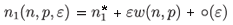
and replacing n1 by this expression in (6). In particular, we obtain
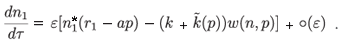
We can also consider 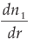 as
as
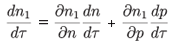
which gives, since 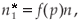

We now identify the terms of order (ε) in both formulae, which gives
w(n, p) = n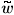 (n, p)
(n, p)
with
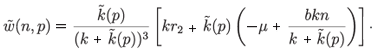
We finally obtain the following aggregated model:
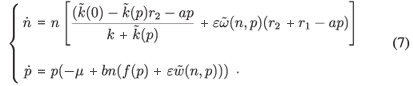
Here, we see that if p = 0, for n ≠ 0, 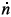 = 0 if and only if
= 0 if and only if 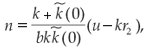 so the non-isolated singularities along the n-axis disappear with this development, and another positive equilibrium can appear. Since the case λ = 0 is minor and more complex, we will not take it further in this study and this article.
so the non-isolated singularities along the n-axis disappear with this development, and another positive equilibrium can appear. Since the case λ = 0 is minor and more complex, we will not take it further in this study and this article.
If it exists, the non-trivial equilibrium point (n*, p*) verifies
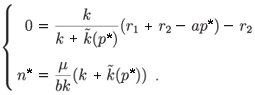
The Jacobian matrix associated with the system is
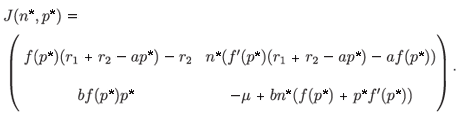
Since 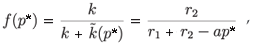
we then have