Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Science
versión On-line ISSN 1996-7489
versión impresa ISSN 0038-2353
S. Afr. j. sci. vol.104 no.3-4 Pretoria mar./abr. 2008
RESEARCH ARTICLES
Stature estimation from bones of South African whites
Manisha R. DayalI, *, **; Maryna SteynII; Kevin L. KuykendallIII, ***
ISchool of Anatomical Sciences, Faculty of Health Sciences, University of the Witwatersrand, 7 York Road, Parktown 2193, South Africa
IIDepartment of Anatomy, University of Pretoria, P.O. Box 2034, Pretoria 0001, South Africa
IIISchool of Anatomical Sciences, Faculty of Health Sciences, University of the Witwatersrand, South Africa
ABSTRACT
Stature reconstruction from skeletal remains forms part of the forensic anthropological analysis for the purpose of identification of the individual. The aim of this study was to derive regression formulae for the estimation of total skeletal height, and thereafter to predict stature in South African whites using long bone lengths. The sample comprised 98 white male and 71 white female skeletons from the Raymond A. Dart Collection of Human Skeletons and the Pretoria Bone Collection. For each individual, total skeletal heights and maximum long bone lengths were measured and used to produceunivariate regression formulae, with resulting correlations (r) ranging between 0.56 and 0.96. The lowest standard error of estimate (1.75 for females, 1.92 for males) was obtained when the lumbar spine, femur and tibia were used in combination, while the highest SEE (5.21 for females, 5.54 for males) was found when the lumbar spine was used on its own. Recently published corrections for soft tissue additions to obtain living height from total skeletal height make these kinds of formulae more usable, and will reduce the problem of underestimation. The derived formulae are population specific and are designed for use in forensic skeletal analyses of South African whites, but are also generally relevant to theoretical and practical issues in forensic anthropology.
Introduction
Forensic anthropology encompasses the examination of skeletal remains for the purposes of identification. It is a sub-field of physical anthropology that has medico-legal implications. The traditional goal of forensic anthropology is to identify human remains once they have been skeletonized, although the forensic anthropologist may be confronted with burned remains, hair samples, footprints, fingerprints, blood or any other tissue sample for blood typing and DNA profiling.1–3 Included in the typical forensic anthropological analysis is the determination of age, sex, race and ante-mortem stature of the unknown individual.
Stature is usually estimated by employing either the anatomical or the mathematical method. The anatomical method estimates total skeletal height, and was initially introduced by Dwight in 1894 (cited in Lundy4). In 1956 Fully5 reintroduced the method with slight variation and it became known as Fully's procedure. This method is based on the summed heights of skeletal elements that contribute to stature in humans. The skeletal elements measured in this method are the cranium, vertebrae, femur, tibia, talus and calcaneus. These represent the elements that contribute to stature,4,5 and their measurements are summed to calculate total skeletal height. To calculate the living stature of an individual using the anatomical method, correction factors that compensate for soft tissue also need to be added.4–6 The main disadvantage of the anatomical method is that a nearly complete skeleton is needed for stature estimation.
The mathematical method, on the other hand, makes use of one or more bone lengths to estimate the stature of the individual. This method employs bone length and stature tables, and regression formulae to estimate total skeletal height or living stature from long bone lengths. Initial research was carried out by many investigators from the 1700s like Sue (1755), Orfila (1821), Beck (1823), Rollet (1888), and Manouvrier (1893) (cited in Stewart1). In 1899, Karl Pearson developed the first formal stature regression formulae.7
To use the mathematical method, the bone length measurement is substituted into a regression equation. The outcome of the equation calculated gives either the total skeletal height or the living stature. This depends upon the equation(s) employed and whether the soft tissue and ageing correction factors were included into the equation. The obvious advantage of this method is that a single bone can be used to estimate the stature of an individual. The main disadvantage of the mathematical method is that different regression formulae are required for different populations, for each different bone and also separately for each sex. This is because variation in body proportions exists, making these formulae population and sex specific.6, 8–11
Regression formulae derived from the major long bones are generally considered to be more accurate than those utilizing other bones such as the skull12,13 or hand and foot bones.14–17 Long bones that make up the greatest proportion of stature, that is, the femur and tibia, are also more accurate than the humerus and ulna.9 Other skeletal elements that have been used to estimate stature include the clavicle.18
The stature regression formulae derived so far and that are commonly used for South Africans of European extraction have been based on either American8,11 or European10,19 populations. As mentioned above, regression formulae are population and sex specific due to genetic differences, isolation, differences in bio-cultural history, and other factors.6,8–11 Stature estimation studies that have been carried out on South African populations include those of Lundy,6 Lundy and Feldesman,9 Bidmos and Asala,20 and Ryan and Bidmos.21 These regressions were developed for South African blacks, and stature estimation from skeletal remains representing South African whites is thus not available. Currently, the only study carried out on South African whites uses calcaneal22 and tibial measurements.23 In addition, the white populations from South Africa are historically of European descent, primarily from the Netherlands, but also from France, Germany, Great Britain and Portugal. Recent studies indicate that South African whites have become osteologically distinguishable from white or Caucasoid populations in Europe and North America,24–26 most likely due to factors such as temporal change, founder effect, and admixture.
The aim of this study was to collect data and calculate regression formulae for total skeletal height from long bones of South African whites, as represented in the Raymond A. Dart Collection of Human Skeletons and the Pretoria Bone Collection. The total skeletal height was then used to estimate the living stature once values for soft tissue are added.
Materials and methods
Skeletons from the Raymond A. Dart Collection of Human Skeletons (School of Anatomical Sciences, University of the Witwatersrand) and the Pretoria Bone Collection (Department of Anatomy, University of Pretoria) were used to collect metric data in this study. Both the Dart collection and the Pretoria collection are still growing and skeletons are being added continuously. A total of 169 skeletons of known individuals were measured, including 98 white males and 71 white females between the stated ages of 25 and 70 years at death. By convention, the left bones in each skeleton were measured, although the right bones were substituted when the left was abnormal or missing. Any skeleton that showed features that would affect the measurements, such as pathology, surgical procedures, or any skeletal abnormality or deformity was not used in this study as this may influence the measurements (for example, a fractured bone may have healed badly and became shorter).
The initial step of the study was to calculate 'total skeletal height' of each skeleton using Fully's anatomical method.4,5 This was necessary because the living statures for the skeletal sample are not recorded, and not all cadavers had recorded lengths. This thus allows for regressing long bone lengths against total skeletal height following the method by Lundy.6 These measurements included the basi-bregmatic height of the cranium, the anterior body heights from the second cervical vertebra (C2) to the fifth lumbar vertebra (L5), the anterior body height of the first sacral vertebra (S1), the oblique/physiological length of the femur, maximum length of the tibia (including the malleolus), and the articulated height of the talus and calcaneus. In addition to the lower limb long bones, four other long bone measurements were taken to derive regression formulae for total skeletal height. These included the maximum length of the humerus, radius, ulna and fibula. All measurements were taken as defined by Martin & Knuβmann,27 and using standard anthropometric techniques. Table 1 gives a list of the measurements, definitions and also the techniques used when measuring these bones. Descriptive statistics were produced on all data using the Statistical Package for Social Scientists (SPSS Inc., Chicago, IL), and significance of the differences between the sexes calculated by means of an independent sample t-test. The F-ratio for Levene's test was also added to test for equality of variance. Univariate analyses using the long bone lengths were regressed against the total skeletal heights. Analyses included regressions from single bones as well as combinations from various bones, such as the lumbar spine (sum of lumbar vertebrae from L1 to L5), femur and tibia. All were calculated using the simple linear regression based on the least-squares method. These were regressed against the total skeletal heights that were calculated using Fully's method.
To calculate the living stature, soft tissue correction factors need to be added and ageing factors need to be subtracted from the total skeletal height. Fully's correction factors were used in previous studies (e.g. Lundy & Feldesman9), but it has been suggested that these correction factors may underestimate the reconstructed heights.31,32 Recently, Raxter et al.33 confirmed this and provided new correction factors, which are adopted in this study. These correction factors are:
Living stature = 1.009 × total skeletal height – 0.0426 × age + 12.1
or
Living stature = 0.996 × total skeletal height + 11.7.
The ageing factor is included because it has been shown that stature decreases with advancing age, mostly due to compression of the vertebrae.5,34 The formula which includes correction for age should thus be used in individuals over the age of 30 years.
Results
Table 2 presents the descriptive statistics of the long bones. As might be expected, the mean long bone lengths of males are significantly longer (P > 0.05) than the mean values for the females. The standard deviations of the mean for male and female variables demonstrate comparable ranges from 1.46 cm for the radius to 2.66 cm for the femur in males, and from 1.40 cm for the radius to 2.19 cm for the femur in females. Except for the femur length all other bone measurements showed equal variance (F-ratio = 4.79).
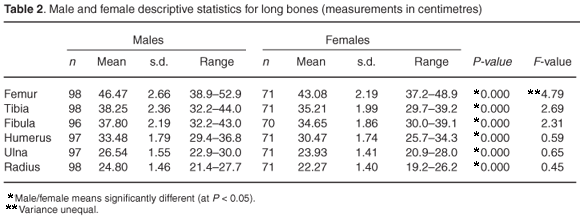
Linear regression formulae in the form of y = c + mx ± standard error of estimate, to estimate total skeletal height from single bones, are presented. Tables 3 and 4 present the univariate regression formulae for single bones and bones in combination for South African white males and females, respectively.
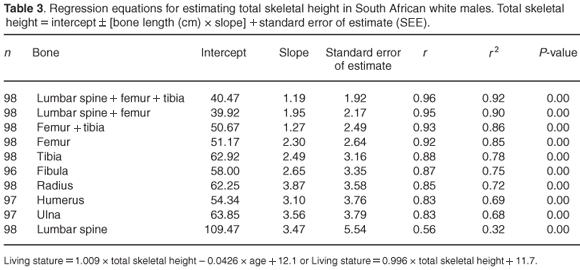
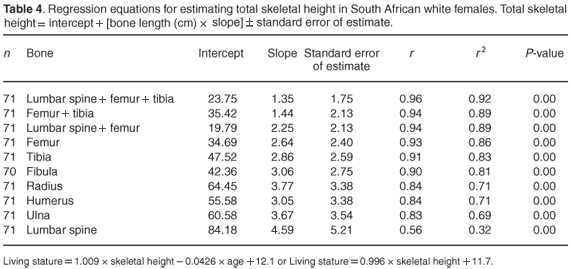
Femur measurements demonstrate the highest correlations with total skeletal height. All correlations involving the femur are 0.92 or above in males, while those in females are 0.93 or above. All lower limb bone correlations for the females are also higher than those of the males, but this is not true for the upper limb bones.
The most accurate regression equation is indicated by the formula that contains the lowest standard error of estimate.6 Thus, in both males and females in this study a combination of the lumbar spine, femur and tibia should be used for calculation of the total skeletal height whenever these elements are available. The correlations tend to be greater where combinations of bones rather than a single long bone length were used, indicating that it is preferable to estimate total skeletal height using more than one bone where possible.8 This holds true for both males and females.
The standard error of estimates for the lumbar vertebrae consistently shows the largest value in males and females, and indeed, the correlation with total skeletal height is very poor. The formula for the lumbar vertebrae would thus only be considered when just the lumbar vertebrae are available for stature estimation.
Discussion
During identification of skeletal remains, general demographic characteristics are determined first. These characteristics include the age, sex and race of the individual. To narrow the number of possibilities further, and thus increase the possibility of identification, factors of individualization are determined, which include stature. For many years the formulae of Trotter & Gleser11,35 have been used most frequently for stature estimation. However, many researchers6,9,11 have cautioned that formulae used to estimate stature should be specifically derived for each different population. It was with this in mind that this study was carried out for a South African white population, and estimated living stature was calculated from a single bone or a combination of bones, as would pertain to a forensic case. Thus, the regression formulae presented are applicable in a practical sense specifically to the South African population, but their use and comparison with other such regionally-derived results are relevant to general practical and theoretical issues in forensic anthropology and human biology.
When estimating stature it has been accepted for a long time that Fully's anatomical method can be used on any population with the soft tissue correction factors being common for all populations.32 These values for soft tissue have also been used by Lundy and Feldesman9 in their formulae for stature estimates in South African blacks. However, even during the course of the present study before the paper by Raxter et al.,33 it was evident that the actual living stature was underestimated. This same objection was raised by other researchers.31,32 The revised values for soft tissue correctional factors33 therefore are of great value, and will contribute towards better estimates using the formulae proposed in this study.
The stature estimates obtained using the formulae derived from the present study are the most appropriate formulae available for South African white skeletal remains. They now also need to be tested on skeletal samples from other parts of the country. The regression formulae using combinations of bone lengths show much better correlation with total skeletal height than those using single bones, as has been shown in previous studies.6,9 This finding reaffirms that stature estimation is more accurate when using more than one bone. The correlations of the combinations of the lumbar vertebrae ('lumbar spine'), femur and tibia illustrate this by having the highest correlation values. The correlation of the lumbar spine, on its own, is very poor and should only be used in cases where the long limb bones are not available. Since the lower limb bones are a direct anatomical component of 'stature', they provide a more accurate basis for total skeletal height estimation compared to the upper limb bones.
The usefulness of regression equations is generally assessed on the basis of their standard error of estimates. A comparison of the standard error of estimates for the different bones used in stature estimation indicates that the long bones provide more accurate estimates. In this study, the standard error of estimates ranged from 2.40 to 3.79 cm for the long bones, while other studies of long bones show standard errors of estimates that are comparable or slightly higher; for example, the study by Trotter and Gleser11 display values of 2.99 to 4.45 cm for whites, 2.25 to 3.09 cm by Dupertuis and Hadden,8 and 2.77 to 3.83 cm by Lundy and Feldesman.9 The results from other studies using the other bones of the body include standard errors of estimates of 5.89 to 7.28 cm for the skull,13 5.30 to 5.49 cm for the vertebral column,36 5.10 to 8.14 cm for metacarpals,14,15 4.65 to 7.60 cm for metatarsals,17 and 4.13 to 6.07 cm for the talus and calcaneus.16,20 This indicates that the long limb bones produce the lowest error of estimates (from single elements) and therefore should be used as the first preference to estimate stature whenever possible. The standard error of estimates reported here (for our study) is low because it applies to total skeletal height whereas the other studies probably mention the standard error of estimate for derived living stature, although this is not always clear from the published results.
A secular trend for an increase in stature has been noted worldwide, and has also been discussed for South African populations.25,37,38 A recent report on stature in South Africans39 also indicated a possible weak secular trend. It is therefore important that these regression formulae should be revised continuously. The skeletons used in this study cover a wide range of birth dates, but many of the skeletons used were derived from human skeletal collections (the Raymond A. Dart Collection of Human Skeletons and the Pretoria Bone Collection), which are continuously adding skeletons to the collection,40 thus also including the most recent skeletons of South African whites available in the country.
In this study, we used Fully's method to estimate total skeletal height and thereafter to derive formulae for use in skeletal samples of South African whites, where only some skeletal elements, and particularly the long limb bones, are available. It is recommended that these formulae be used for stature reconstructions of South African whites, while that of Lundy & Feldesman9 are still the most applicable for South African blacks. However, the revised values to compensate for soft tissue33 should also be applied after the skeletal height has been calculated using the Lundy & Feldesman formulae for South African blacks.
We thank the University of the Witwatersrand for a bursary provided towards completing this study. Our heartfelt appreciation goes to Beverley Kramer and Jan Meiring for permission to use the collections, Elijah Mofokeng for accession to the specimens, and John Lundy for all his advice and motivation during the study.
1. Stewart T.D. (1979). Essentials of Forensic Anthropology. Charles C. Thomas, Springfield, Ill. [ Links ]
2. Fairgrieve S.I. (1999). Forensic Osteological Analysis: A Book of Case Studies. Charles C Thomas, Springfield, Ill. [ Links ]
3. Klepinger L.L. (2006). Fundamentals of Forensic Anthropology. Wiley, New York. [ Links ]
4. Lundy J.K. (1985). The mathematical versus anatomical methods of stature estimate from long bones. Am. J. Forensic. Med. Pathol. 6, 73–76. [ Links ]
5. Fully G. (1956). New method of determination of the height. Ann. Med. Leg. Criminol. Police. Sci. Toxicol. 36, 266–273. [ Links ]
6. Lundy J.K. (1983). Regression equations for estimating living stature from long limb bones in the South African Negro. S. Afr. J. Sci. 79, 337–338. [ Links ]
7. Pearson K. (1899). Mathematical contributions to the theory of evolution. On the reconstruction of the stature of prehistoric races. Phil. Trans. R. Soc. Lond. A 192, 169–244. [ Links ]
8. Dupertuis C.W. and Hadden J. (1951). On the reconstruction of stature from long bones. Am. J. Phys. Anthropol. 9, 15–54. [ Links ]
9. Lundy J.K. and Feldesman M.R. (1987). Revised equations for estimating living stature from long bones of the South African Negro. S. Afr. J. Sci. 83, 54–55. [ Links ]
10. Olivier G., Aaron C., Fully G. and Tissier G. (1978). New estimations of stature and cranial capacity in modern man. J. Hum. Evol. 7, 513–518. [ Links ]
11. Trotter M. and Gleser G.C. (1952). Estimation of stature from long bones of American Whites and Negroes. Am. J. Phys. Anthropol. 10, 463–514. [ Links ]
12. Introna F., Di Vella G. and Petrachi S. (1993). [Determination of height in life using multiple regression of skull parameters]. Boll. Soc. Ital. Biol. Sper. 69, 153–160. [ Links ]
13. Chiba M. and Terazawa K. (1998). Estimation of stature from somatometry of skull. Forensic Sci. Int. 97, 87–92. [ Links ]
14. Musgrave J.H. and Harneja N.K. (1978). The estimation of adult stature from metacarpal bone length. Am. J. Phys. Anthropol. 48, 113–119. [ Links ]
15. Meadows L. and Jantz R.L. (1992). Estimation of stature from metacarpal lengths. J. Forensic Sci. 37, 147–154. [ Links ]
16. Holland T.D. (1995). Estimation of adult stature from the calcaneus and talus. Am. J. Phys. Anthropol. 96, 315–320. [ Links ]
17. Byers S.N., Akoshima K. and Curran B. (1989). Determination of adult stature from metatarsal length. Am. J. Phys. Anthropol. 79, 275–279. [ Links ]
18. Jit I. and Singh S. (1956). Estimation of stature from clavicles. Indian J. Med. Res. 44, 137–155. [ Links ]
19. De Mendonça M.C. (2000). Estimation of height from the length of long bones in a Portuguese adult population. Am. J. Phys. Anthropol. 112, 39–48. [ Links ]
20. Bidmos M.A. and Asala S.A. (2005). Calcaneal measurement in estimation of stature of South African blacks. Am. J. Phys. Anthropol. 126, 335–342. [ Links ]
21. Ryan I. and Bidmos M.A. (2007). Skeletal height reconstruction from measurements of the skull in indigenous South Africans. Forensic Sci. Int. 167, 16–21. [ Links ]
22. Bidmos M.A. (2006). Adult stature reconstruction from the calcaneus of South Africans of European descent. J. Clin. Forensic Med. 13, 247–252. [ Links ]
23. Chibba K. and Bidmos M.A. (2007). Using tibia fragments from South Africans of European descent to estimate maximum tibia length and stature. Forensic Sci. Int.169, 145–51. [ Links ]
24. Steyn M. and Iscan M.Y. (1998). Sexual dimorphism in the crania and mandibles of South African whites. Forensic Sci. Int. 98, 9–16. [ Links ]
25. Henneberg M. and van den Berg E.R. (1990). Test of socioeconomic causation of secular trend: stature changes among favored and oppressed South Africans are parallel. Am. J. Phys. Anthropol. 83, 459–465. [ Links ]
26. Louw G.J. and Henneberg M. (1997). Lack of secular trend in adult stature in white South African males born between 1954 and 1975. HOMO 48, 54–61. [ Links ]
27. Martin R. and Knussman R. (1988). Anthropologie: Handbuch der vergleichenden Biologie des Menschen. Gustav Fischer Verlag. [ Links ]
28. McMinn R.M.H., Hutchings R.T. and Logan B.M. (1989). A Colour Atlas of Foot and Ankle Anatomy, 2nd edn. Wolfe Medical Publications, Weert, the Netherlands. [ Links ]
29. Weissman S.D. (1989). Radiology of the Foot, 2nd edn. Williams & Wilkins, Baltimore. [ Links ]
30. Gentili A., Masih S., Yao L. et al. (1996). Pictorial review: foot axes and angles. Br. J. Radiol. 69, 968–974. [ Links ]
31. King K.A. (2004). A test of the Fully anatomical method of stature estimation (abstract). Am. J. Phys. Anthropol. (Suppl.) 38, 125. [ Links ]
32. Bidmos M.A. (2005). On the non-equivalence of documented cadaver lengths to living stature estimates based on Fully's method on bones in the Raymond A. Dart Collection. J. Forensic Sci. 50, 501–506. [ Links ]
33. Raxter M.H., Auerbach B.M. and Ruff C. B. (2006). Revision of the Fully technique for estimating statures. Am. J. Phy. Anthropol. 130, 374–384. [ Links ]
34. Galloway A. (1988). Estimating actual height in the older individual. J. Forensic Sci. 33, 126–136. [ Links ]
35. Trotter M and Gleser G.C. (1958). A re-evaluation of estimation of stature based on measurements of stature taken during life and of long bones after death. Am. J. Phys. Anthropol. 16, 79–123. [ Links ]
36. Tibbetts G.L. (1981). Estimation of stature from the vertebral column in American Blacks. J. Forensic Sci. 26, 715–723. [ Links ]
37. Tobias P.V. (1975). Stature and secular trend among southern African Negroes and San (Bushmen). S. Afr. J. Med. Sci. 40, 145–164. [ Links ]
38. Tobias P.V. (1985). The negative secular trend. J. Hum. Evol. 14, 347–356. [ Links ]
39. Steyn M. and Smith J.R. (2007). Interpretation of ante-mortem stature estimates in South Africans. Forensic Sci. Int. 171, 97–102 [ Links ]
40. L'Abbe E.N., Loots M. and Meiring J.H. (2005). The Pretoria Bone Collection: a modern South African skeletal sample. HOMO 56, 197–205. [ Links ]
Received 13 April 2007. Accepted 14 March 2008.
* Author for correspondence. E-mail: mad.phd@gmail.com
** Present address: Anatomical Sciences, School of Medical Sciences, Medical School North, The University of Adelaide, South Australia, 5005 Australia
*** Present address: Department of Archaeology, University of Sheffield, Sheffield, U.K.














