Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.104 n.1-2 Pretoria Jan./Feb. 2008
RESEARCH ARTICLES
SERGE: a spatially explicit generator of local rainfall in southern Africa
Dirk EisingerI; Kerstin WiegandII, *
IDepartment of Ecological Modelling, UFZ-Centre for Environmental Research, P.O. Box 500136, 04301 Leipzig, Germany
IIInstitute of Ecology, Friedrich Schiller University, Dornburgerstr. 159, 07743 Jena, Germany
ABSTRACT
This article describes the features of SERGE, a stochastic, spatially explicit tool for the simulation of daily rainfall in arid environments. Rainfall data (either raw or produced by a rainfall generator) are frequently available on a daily basis but at low spatial resolution. Furthermore, although the rainfall characteristics of a given small area may vary little when averaged over the long term, rainfall does vary substantially on a daily time scale. It is exactly this short-term, small-scale variation that is of interest to modellers in many applications. A tool is needed therefore that generates spatio-temporal rainfall estimates based on only temporal data. To fill this gap, we developed SERGE using an ad hoc approach. Based on known characteristics of rainfall at a point, SERGE projects spatially homogeneous daily rainfall produced by a rainfall generator into spatially heterogeneous estimates by distributing clouds of fixed size and random position. Our algorithm preserves the long-term rainfall characteristics at each point, but introduces spatial autocorrelation of variable length. SERGE provides a simple and flexible tool for the simulation of spatio-temporal rainfall to be integrated into other models. SERGE is intended for modellers wanting to investigate the effect of spatially variable rainfall in their system. Given the importance of spatial variability in arid environments, this should be of interest to scientists in the fields of ecology, range management, agriculture, climate change, and hydrology.
Introduction
Rainfall is among the most important drivers of the spatio-temporal distribution of flora and fauna. Rainfall therefore has important consequences for potential land use and so for people's livelihoods. Worldwide, inter-annual rainfall variation is inversely related to long-term average rainfall.1 Inter-annual rainfall variability is therefore of particular interest in arid and semi-arid environments, where productivity is low and land use is dominated by rangelands. Ecologists currently lead a debate on the dynamic forcing mechanisms driving rangeland systems. For example, traditional range management concepts assume the existence of an equilibrium livestock carrying capacity mainly forced by mean annual rainfall of the region and by biotic feedbacks of livestock on vegetation productivity. However, the 'new rangeland science' views rangelands as non-equilibrium systems driven primarily by stochastic abiotic factors, notably variable rainfall, which result in highly variable primary production.2 Furthermore, simulation models that apply different rainfall scenarios to agricultural crop models show that inter-annual rainfall variability can have substantial negative or positive effects on crop yields.3
In contrast to temporal variability, intra-annual spatial variability of rainfall has received very little attention even though rainfall in arid and semi-arid environments is often patchily distributed with spatial cells as small as 1 km2.4-8 Localized convective processes lead to summer anomalies that are more spatially complex than in winter, when broad-scale synoptic and frontal processes cause precipitation.9 This spatial variability of rainfall affects the spatial distribution of plant and animal communities. For example, germination and early survival of many plant species depends critically on frequent but not necessarily high rainfall during early summer.10 In this case, plant population and community dynamics in areas as small as a few hectares may depend on the spatio-temporal mosaic of rainfall because its spatial distribution is determined by the spatio-temporal overlap of several rain cells.11 The effects of spatially complex rainfall on vegetation range from straightforward consequences such as spatially heterogeneous grass production to complicated outcomes that mediate the coexistence of trees and grasses in arid savannas.8,11,12 The resulting spatio-temporal distribution of plants can have pronounced effects on the distribution of animals, for example, of larks,13 rodents,14 and gorillas.15 Moreover, the spatio-temporal distribution of rainfall is likely to have notable effects on species diversity.16
Our original interest is savanna ecology, specifically the effect of fine-scale variability of rainfall on tree-grass dynamics. A new hypothesis to explain tree-grass coexistence is the patch-dynamics theory,12 which proposes that savannas can be interpreted as patch-dynamic systems where landscapes are composed of many patches in different states of cyclical transition between woody and grassy dominance. Transition is spatially asynchronous within patches and is driven by self-thinning and localized rain events. Self-thinning arises from the density-dependent mortality of woody plants and drives the transition of a tree-dominated to a grass-dominated patch. Repeatedly overlapping rain events may induce mass germination of a tree cohort and promote the transition of a grassy patch to woody dominance. To study the tree-grass ratio of patch-dynamic savannas, therefore, daily rainfall data of fine-scale spatial resolution are needed. Generators of daily rainfall occurrence and amounts like the models by Stern and Coe,17 Zucchini et al.18 and others19 provide us with temporally autocorrelated rainfall at the scale of one day. To represent spatial variability, current alternatives are to use the same rainfall across the entire simulated areathat is, 100% spatial autocorrelation or to use independent rainfall data for different locations within the areathat is, without spatial autocorrelation. However, the effect of spatially correlated rainfall on ecosystem dynamics (e.g. the role of savanna patch dynamics for tree-grass coexistence) is probably best investigated using rainfall data of variable autocorrelation lengths. Existing spatio-temporal rainfall models20-23 are difficult to apply in this situation because they need to be fitted to spatio-temporal data which frequently are not available.
To bridge the gap between the need to study the effects of spatially varying rainfall and the absence of spatio-temporal data, we present SERGE (for Spatially Explicit Rainfall GEnerator), a tool for the simulation of spatially autocorrelated rainfall on a daily basis. As a result of our specific interest in southern Africa, the generator is based on the non-spatial Zucchini model for daily rainfall over the subcontinent.18,24,25 SERGE maintains the temporal distribution pattern predicted at every location by Zucchini's algorithm while showing spatial variability of variable autocorrelation lengths.
Methods
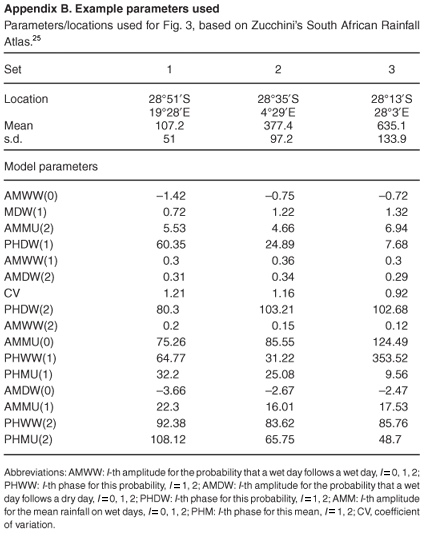
The Zucchini model comprises 16 parameters and has been calibrated in terms of daily rainfall records throughout South Africa.24,26 The model is therefore a reliable representation of temporal rainfall. The rainfall characteristics of the Zucchini model vary from station to station, each one of which may be regarded as representative of the average rainfall over a certain area. However, a spatial component in the sense of how rainfall varies within such an area is missing. We designed SERGE to generate spatially variable rainfall estimates of different spatial correlation, while preserving the temporal rainfall distribution of the Zucchini24 model in any single cell. In SERGE, spatial variability is introduced parsimoniously by invoking clouds under the simplifying assumption of constant cloud size on a given day, with cloud being the area which will receive rain in one of several events each rainday. Compared with the Zucchini model, this requires just one additional parameter that describes cloud size (Figure, Appendix A).
In short, for a given day, SERGE calculates a regional rainfall amount on the basis of an adjusted Zucchini24 algorithm. This rain is distributed in the modelled area using several randomly positioned rain clouds. The resulting rainfall of each individual cell reproduces the characteristics of the original Zucchini model. The rules for the necessary adjustments to the Zucchini algorithm and their derivation are presented in Appendix A.
The need for the adjustment arises from the distribution of rainfall over the region as a result of several randomly distributed clouds. Instead of assuming the same amount of rainfall produced by one large cloud for the entire region, SERGE divides this cloud into several smaller ones of equal size and places them in random positions [Equation (1), Appendix A]. Consequently, on a given rainday not all the cells receive rain, while some cells may receive rain twice on that day (Fig. 1a). To ensure that the locally distributed rainfall reflects the long-term average, several constraints are necessary. The rainfall probability in the region must be higher than its probability in a cell [Equations (10) and (11), Appendix A] and the rainfall amount per cloud must be less than the average amount of rain received in a cell [Equation (12), Appendix A].
All results shown in this paper are based on a modelled area of 100 cells in length. Thus, the area covered by a single cloud equals cloud size divided by 100. Note that for ease of visualization the Results section presupposes that rainfall changes in one spatial direction only. However, the cloud model as presented in Appendix A is not contingent on dimensionalitySERGE is equally valid for rainfall varying in two-dimensional space. Moreover, there is no restriction on the shape of clouds and even the shape can change within a day as the rule derivation depends only on cloud cover staying constant during a day and on the random placement of the clouds.
Results
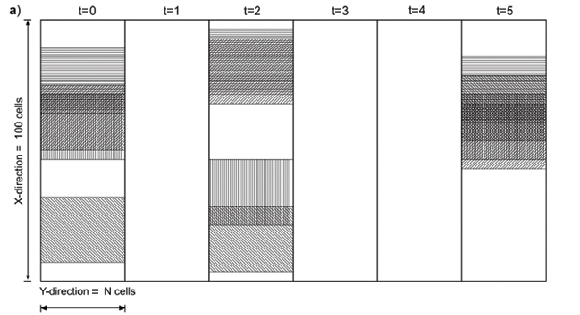
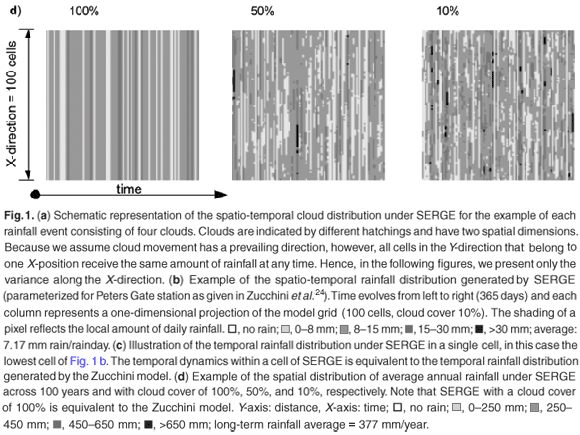
Because all cells along the Y-axis in Fig. 1a receive the same amount of rainfall, we focus on one spatial dimension (the X-axis; Fig. 1b-d). Spatio-temporal daily rainfall generated by SERGE shows a high spatial variability and a typical correlation length that reflects the underlying cloud size (Fig. 1b, cloud size 10 cells). This is in contrast to rainfall that is equally distributed in space (Fig. 1c). Figure 1c is actually an extended representation of the temporal distribution of rainfall in a single cell. Rain falls far more often somewhere in the region (Fig. 1b) than it does in any single cell (Fig. 1c). As a consequence of the spatial variability of daily rainfall in SERGE, annual rainfall is also patchy. Patchiness increases with decreasing cloud size (Fig. 1d).
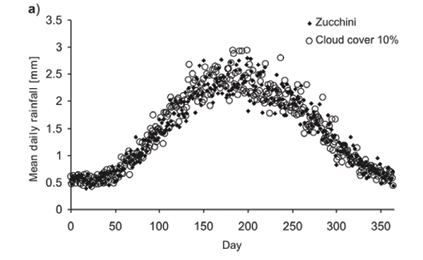
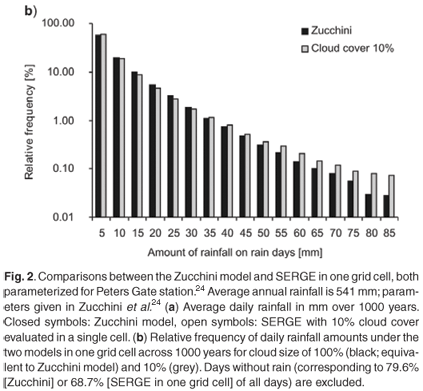
Average daily rainfall of the Zucchini model in a cell is largely preserved by SERGE (Fig. 2a). However, the frequency distribution of daily rainfall for each cell differs slightly from that in the Zucchini model (Fig. 2b). This is due to the possibility of several clouds covering the same cell. This causes an increase in the probability of a single cell receiving very high or, conversely, very small amounts of rain on a single day (Fig. 2b; note the logarithmic scale).
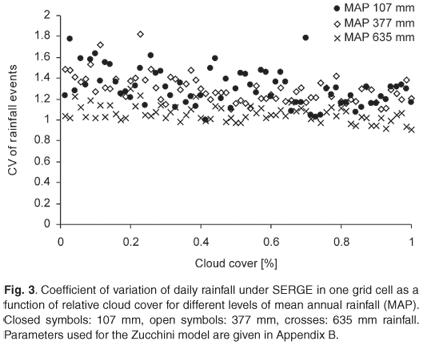
Under SERGE, the coefficient of variation of daily rainfall in one grid cell decreases slightly with cloud size (Fig. 3). In addition, the coefficient of variation tends to be smaller for cells with high long-term average rainfall. This is due to the greater probability of rainfall in a region, making it more likely that all cells have been under a cloud at least once.
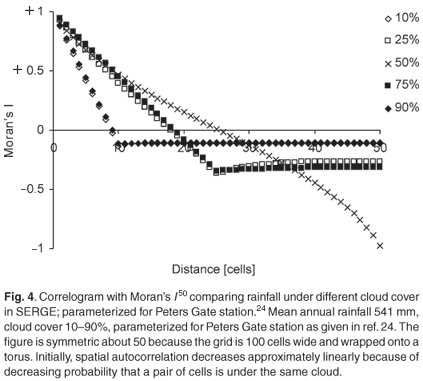
The daily rainfall correlation between cells generally decreases with distance between cells (Fig. 4). The lowest correlation is reached at a distance equal to cloud size. At this distance, two cells are never under the same cloud. The correlation increases slightly thereafter because of the increasing probability that several clouds will lie between two cells and, hence, that neither cell will receive rain.
Discussion
Mathematical and computer models of environmental systems commonly require long-term rain data as model input. Given the limited duration of measured time series, most models are run with synthetic rain data generated by stochastic models that create rainfall with statistical characteristics similar to those of historical data measured at individual rain gauges.27,28 A relatively recent trend in daily rainfall generators is the modelling of daily rainfall at multiple locations.29,30 These multi-site generators preserve the characteristics of historical data measured at a network of rain-gauge stations. For many applications, however, spatially continuous rainfall would be more useful. Hitherto, there have been only a few statistical models that generate rainfall continuously in space.31 Dynamic regional atmospheric models (RCMs) provide spatially continuous rainfall, yet at a spatial horizontal resolution too low to address many ecological and hydrological questions.32-34 We therefore developed SERGE to generate spatially autocorrelated high-resolution rainfall efficiently, based on one of many non-spatial rainfall generators.24 One might criticize our failure to compare our model results with data from a spatial network of rain gauges. However, there is a severe lack of data at the spatial scales we examined, namely several hectares to a few square kilometres. We hope that in the near future there will be sufficient data (such as from satellites) against which to verify SERGE. Our model currently provides the means to test the importance of spatial variability in rainfall for specific applications and at specific locations. If the need for more quantitative predictions arises, the results based on SERGE should be an incentive to collect more detailed data.
We based SERGE on the Zucchini24 rainfall model because the latter is commonly applied in spatially explicit simulation models of plant and animal dynamics in the arid and semi-arid parts of South Africa.35-38 Depending on the species of concern, these models are often of interest for nature conservation39 and/or range management.8,40 With increasing computing power, it is now feasible to simulate areas large enough to encompass spatial rainfall variability, especially for arid environments with very patchy rainfall. Given the importance of rainfall's spatial variability in arid and semi-arid environments, many of these models are likely to benefit from applying spatially explicit rainfall generators such as SERGE.
Whether it is indeed necessary to include spatially explicit rainfall in an ecological simulation of plant or animal dynamics depends mainly on the spatio-temporal scales of both the simulation model and the species modelled. If the spatial extent of a simulation model is small (say, <1 ha), spatially homogeneous rainfall is a good approximation of reality. If a species is able to integrate rainfall over time, it may be sufficient to model rainfall exclusively over time, such as on an annual basis. However, some life stages may be more sensitive to daily rainfall than others. For example, the germination of savanna woody plants is highly sensitive to the daily distribution of rainfall.10,41 To quantify the uncertainties associated with the potential role of the spatial variation of rainfall in impact models, we recommend comparing simulations with and without spatially variable rainfall.
SERGE may also help to understand better the frequency and occurrence of flash floods in arid environments by linking them with hydrological models operating on spatially explicit information on topography, land cover, and soil properties.42,43 Furthermore, we foresee some interesting applications in the investigation of global change. This is highly relevant especially if rainfall variability is expected to increase further with climate change.44 For example, SERGE can be integrated in spatially explicit models of plant and animal persistence in arid and semi-arid environments39,45,46 or in models of carbon and nutrient cycles.47 This application, however, depends on information on how rainfall characteristics are expected to change.48,49 A more straightforward approach is therefore to couple SERGE with RCM climate projections. RCM models have low spatial resolution owing to computational constraints. SERGE may be used to simulate rainfall at a higher spatial resolution, however, while maintaining the rainfall characteristics of the driving RCM (just as it presently maintains the main characteristics of the Zucchini model).
This research was supported by the Volkswagen Foundation and the Deutsche Forschungsgemeinshaft. We thank an anonymous reviewer, Aris Moustakas, Walter Zucchini and Matthias Wichmann for comments on early versions of the manuscript, and Peter Walsh for assistance with its preparation.
1. Schulze R.E. (1997). Climate. In Vegetation of Southern Africa, eds R.M. Cowling, D.M. Richardson and S.M. Pierce, pp. 21-42. Cambridge University Press, Cambridge. [ Links ]
2. Gillson L. and Hoffman M.T. (2007). Rangeland ecology in a changing world. Science 315, 53-54. [ Links ]
3. Mearns L.O., Rosenzweig C. and Goldberg R. (1997). Mean and variance change in climate scenarios: methods, agricultural applications, and measures of uncertainty. Climatic Change 35, 367-396. [ Links ]
4. Green G.C. (1969). Variability and probability of rainfall in relation to coefficients of variation of rainfall series. Agrochemophysica 1, 1-8. [ Links ]
5. Sharon D. (1972). The spottiness of rainfall in a desert area. J. Hydrol. 17, 161-175. [ Links ]
6. Sharon D. (1981). The distribution in space of local rainfall in the Namib Desert. Int. J. Climatol. 1, 69-75. [ Links ]
7. Prins H.H.T. and Loth P.E. (1988). Rainfall patterns as background to plant phenology in northern Tanzania. J. Biogeogr. 15, 451-463. [ Links ]
8. Ward D., Saltz D. and Ngairorue B.T. (2004). Spatio-temporal rainfall variation and stock management in arid Namibia. J. Range. Manage. 57, 130-140. [ Links ]
9. Comrie A.C. and Broyles B. (2002). Variability and spatial modeling of fine-scale precipitation data for the Sonoran Desert of south-west Arizona. J. Arid Environ. 50, 573-592. [ Links ]
10. Wilson T.B. and Witkowski E.T.F. (1998). Water requirements for germination and early seedling establishment in four African savanna woody plant species. J. Arid Environ. 38, 541-550. [ Links ]
11. Wiegand K., Ward D. and Saltz D. (2005). Multi-scale patterns in an arid savanna with a single soil layer. J. Veg. Sci. 16, 311-320. [ Links ]
12. Wiegand K., Saltz D. and Ward D. (2006). A patch dynamics approach to savanna dynamics and woody plant encroachment - Insights from an arid savanna. Persp. Plant Ecol. Evol. Sys. 7, 229-242. [ Links ]
13. Fahse L., Dean W.R.J. and Wissel C. (1998). Modelling the size and distribution of protected areas for nomadic birds: Alaudidae in the Nama-Karoo, South Africa. Biol. Conserv. 85, 105-112. [ Links ]
14. Ernest S.K.M., Brown J.H. and Parmenter R.R. (2000). Rodents, plants, and precipitation: spatial and temporal dynamics of consumers and resources. Oikos 88, 470-482. [ Links ]
15. Walsh P.D. and White L.J.T. (2005). Evaluating the steady state assumption: simulations of gorilla nest decay. Ecol. Appl. 15, 1342-1350. [ Links ]
16. Chesson P.L., Gebauer R., Schwinning S., et al. (2004). Resource pulses, species interactions, and diversity maintenance in arid and semi-arid environments. Oecologia 141, 236-253. [ Links ]
17. Stern R.D. and Coe R. (1984). A model fitting analysis of daily rainfall data. J. R. Statist. Soc. A 147, 1-34. [ Links ]
18. Zucchini W. and Adamson P.T. (1984). The occurrence and severity of droughts in South Africa. WRC Report No. 91/1/84. Water Research Commission, Pretoria. [ Links ]
19. Woolhiser D.A. (1992). Modeling daily precipitation - progress and problems. In Statistics in the Environmental and Earth Sciences, eds A.T. Waldon and P. Guttorp, pp. 71-89. Halsted Press, New York. [ Links ]
20. Cox D.R. and Isham V. (1988). A simple spatial-temporal model of rainfall. Proc. R. Soc. Lond. A 415, 317-328. [ Links ]
21. Charles S., Bates B. and Hughes P. (1999). A spatio-temporal model for downscaling precipitation occurrence and amounts. J. Geophys. Res. 104, 31657-31669. [ Links ]
22. Bellone E., Hughes J.P. and Guttorp P. (2000). A hidden Markov model for relating synoptic scale patterns to precipitation amounts. Climate Res. 15, 1-12. [ Links ]
23. Onof C., Chandler R.E., Kakou A., Northrop P., Wheater H.S. and Isham V. (2000). Rainfall modelling using Poisson-cluster processes: a review of developments. Stochastic Environ. Res. Risk Assess. 14, 384-411. [ Links ]
24. Zucchini W., Adamson P. and McNeill L. (1992). A model of southern African rainfall. S. Afr. J. Sci. 88, 103-109. [ Links ]
25. Zucchini W. and Nenadic O. (2006). A web-based rainfall atlas for southern Africa. Environmetrics 17, 269-283. [ Links ]
26. Zucchini W., Nenadic O. and Kratz G. (2003). A web-based South Africa rain atlas. In ISI 2003: 54th Session of the International Statistical Institute, Berlin. [ Links ]
27. Wilks D.S. and Wilby R.L. (1999). The weather generation game: a review of stochastic weather models. Prog. Phys. Geog. 23, 329-357. [ Links ]
28. Srikanthan R. and McMahon T.A. (2001). Stochastic generation of annual, monthly and daily climate data: A review. Hydrol. Earth Syst. Sci. 5, 653-670. [ Links ]
29. Bardossy A. and Plate E.J. (1992). Space-time model for daily rainfall using atmospheric circulation patterns. Water Resour. Res. 28, 1247-1259. [ Links ]
30. Mehrotra R., Srikanthan R. and Sharma A. (2006). A comparison of three stochastic multi-site precipitation occurrence generators. J. Hydrol. 331, 280-292. [ Links ]
31. Leonard M., Metcalfe A.V. and Lambert M.F. (2006). Efficient simulation of a space-time Neyman-Scott rainfall model. Water Resour. Res. 42, Art. No. W11503. [ Links ]
32. Engelbrecht F.A., Rautenbach C.J. de W., McGregor J.L. and Katzfey J.J. (2002). January and July climate simulations over the SADC region using the limited-area model DARLAM. Water S.A. 28, 361-374. [ Links ]
33. Olwoch J.M., Rautenbach C.J. de W., Erasmus B.F.N., Engelbrecht F.A. and van Jaarsveld A.S. (2003). Simulating tick distributions over sub-Saharan Africa: the use of observed and simulated climate surfaces. J. Biogeogr. 30, 1221-1232. [ Links ]
34. Tadross M.A., Gutowski W.J.J., Hewitson B.C., Jack C.J. and New M. (2006). MM5 simulations of interannual change and the diurnal cycle of southern African regional climate. Theor. Appl. Climatol. 86, 63-80. [ Links ]
35. Wiegand T., Milton S.J. and Wissel C. (1995). A simulation model for a shrub ecosystem in the semiarid Karoo, South Africa. Ecology 76, 2205-2221. [ Links ]
36. Jeltsch F., Milton S.J., Dean W.R.J. and Van Rooyen N. (1996). Tree spacing and coexistence in semiarid savannas. J. Ecol. 84, 583-595. [ Links ]
37. Weber G., Jeltsch F., Van Rooyen N. and Milton S.J. (1998). Simulated long-term vegetation response to grazing heterogeneity in semiarid rangelands. J. Appl. Ecol. 35, 687-699. [ Links ]
38. Reineking B., Veste M., Wissel C. and Huth A. (2006). Environmental variability and allocation trade-offs maintain species diversity in a process-based model of succulent plant communities. Ecol. Modell. 199, 486-504. [ Links ]
39. Wichmann M.C., Jeltsch F., Dean W.R., Moloney K.A. and Wissel C. (2003). Implication of climate change for the persistence of raptors in arid savanna. Oikos 102, 186. [ Links ]
40. Graef F. and Haigis J. (2001). Spatial and temporal rainfall variability in the Sahel and its effects on farmers' management strategies. J. Arid Environ. 48, 221-231. [ Links ]
41. Kraaij T. and Ward D. (2006). Effects of rain, nitrogen, fire and grazing on tree recruitment and early survival in bush-encroached savanna, South Africa. Plant Ecol. 186, 235-246. [ Links ]
42. Foody G.M., Ghoneim E.M. and Arnell N.W. (2004). Predicting locations sensitive to flash flooding in an arid environment. J. Hydrol. 292, 48-58. [ Links ]
43. Nezlin N.P. and Stein E.D. (2005). Spatial and temporal patterns of remotely- sensed and field-measured rainfall in southern California. Remote Sens. Environ. 96, 228-245. [ Links ]
44. IPCC (2001). Climate Change 2001: The scientific basis. Contribution of working group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge and New York. [ Links ]
45. Wichmann M.C., Groenveld J., Jeltsch F. and Grimm V. (2005). Mitigation of climate change impacts on raptors by behavioural adaptation: ecological buffering mechanisms. Global and Planetary Change 45, 273-281. [ Links ]
46. Tews J., Esther A., Milton S.J. and Jeltsch F. (2006). Linking a population model with an ecosystem model: Assessing the impact of land use and climate change on savanna shrub cover dynamics. Ecol. Modell. 195, 219-228. [ Links ]
47. Austin A.T., Yahdjian L., Stark J.M., et al. (2004). Water pulses and biogeochemical cycles in arid and semiarid ecosystems. Oecologia 141, 221-235. [ Links ]
48. Engelbrecht F. (2005). Simulations of climate and climate change over southern and tropical Africa with the conformal-cubic atmospheric model. In Climate Change and Water Resources in southern Africa: Studies on scenarios, impacts, vulnerabilities and adaptation, ed. R.E. Schultze. WRC Report 1430/1/05, pp. 57-74. Water Research Commission, Pretoria. [ Links ]
49. Tadross M.A., Jack C.J. and Hewitson B.C. (2005). On RCM-based projections of change in southern African summer climate. Geophys. Res. Lett. 32, L23713. [ Links ]
50. Overmars K.P., de Koning G.H.J. and Veldkamp A. (2003). Spatial autocorrelation in multi-scale land use models. Ecol. Modell. 164, 257-270. [ Links ]
Received 29 June 2007. Accepted 13 January 2008.
* Author for correspondence. E-mail: mail@kerstin.wiegand.de
Appendix A. Description of cloud model
The rainfall data are produced in two steps. First, we obtain the daily target characteristics of the rainfall for a cell from the Zucchini model (Fig. A1). These are pzucchini, the probability of rainfall on day t, and rainzucchini, the amount of rainfall on day t. In a second step, we use pzucchini and rainzucchini to calculate a regional rainfall (pregion) and (raincloud), which is heterogeneously distributed across space. SERGE's algorithm ensures the reproduction of the rainfall characteristics given above, i.e. pcell = pzucchini and raincell = rainzucchini, in each cell.
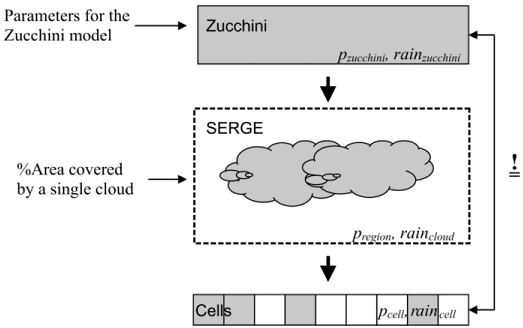
For the first step, the target characteristics for the cell are directly taken from the Zucchini rainfall model,24 which provides us with the daily probability of a rainfall event (pzucchini) and the amount of rainfall per event (rainzucchini). There are two different daily probabilities in the Zucchini model: AMDW (the probability of a wet day following a dry day, here named pdw) and AMWW (the probability of a wet day following a wet day, here named pww), which are used alternately depending on the previous day's condition. In the following, when we speak of the rainfall probabilities (p, pzucchini, pcell, etc.) it will apply to both of the different probabilities: e.g. pcell always should be read both as pdwcell and as pwwcell.
For the second step, we derive below the necessary characteristics for the regional rainfall (pregion, probability of rainfall in the region, and raincloud, amount of rainfall per cloud), which is then distributed using clouds. By 'clouds' we here mean areas which will receive rain in one of several events each rainday. Pregion and raincloud vary with the size of the clouds, hence the derivation starts there.
Rule derivation:
The location of the clouds is determined randomly. We assume periodical border conditions, i.e. a cloud on the border of adjacent cells extends on both sides. This is necessary to ensure that all cells have the same probability of being under a cloud. As long as this is fulfilled and the cloud size is constant throughout that day, clouds may have any size or position. As the area which is covered by one cloud is smaller than the area modelled, we add additional clouds of the same storm depth (raincloud) but different random location until the cumulated area covered by the clouds equals the size of the modelled area. Hence, the number of clouds (NumClouds, including fractions) and the fraction of area which is covered by one cloud (CloudCover) is:
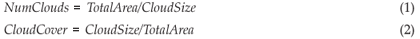
The positions of the clouds vary and some cells are covered by two or more clouds and others not at all. The probability of a cell being under a cloud (probunder_cloud) and getting rain is:

Therefore, the effective daily rainfall probability for a cell would be

As the probability of being under a cloud does not equal one, the probability of a wet day following a dry day (pdw) and of a wet day following a wet day (pww) in a region and cell differ and we need to calculated different pdw and pww values.
One aim is that for each cell the fraction of all days with rainfall, dw, and the fraction of wet days following other wet days, dww, do not differ between the Zucchini and the cloud models. Another is to find regional values of pwwregion and pdwregion for the cloud model that achieve the first aim.
The following equations apply, both regionally and for cells separately:

As mentioned above with respect to clouds, the days with rain somewhere in the region (dwregion) and the raindays in a specific cell (dwcell), differ (pc = probunder _cloud).
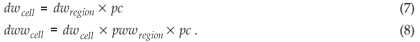
If we want the Zucchini model be fulfilled at the level of the cell (dwzucchini = dwcell and dwwzucchini = dwwcell), it follows that:
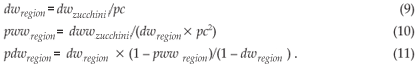
The probabilities are now adjusted. However, since in Equation (9) we have 1/pc more raindays in the region than in the cell, the amount of rainfall in each cloud (raincloud) has to be reduced by this factor to obtain the correct average rainfall for the cell.

Thus, our procedure is as follows:
a) Find the AMDW = pdwzucchini and the AMWW = pwwzucchini of the Zucchini model for each day which corresponds to the desired station, and calculate dwzucchini and dwwzucchini using Equations (5) and (6).
b) Use Equations (9)-11) to find the regional probabilities pdwregion and pwwregion and determine whether it rains on this day.
c) If it does rain, find the amount of rainfall from the Zucchini model24 for that day, multiply it by prob under_cloud [Equation (12)] and distribute it in NumClouds randomly positioned clouds [Equation (1)]. If NumClouds is a non-integer number, use the rounded figure for the number of clouds. The remaining fraction determines the probability of an additional cloud this day.
Using this procedure, one gets the same average rainfall amounts, number of days with rainfall, and number of days with consecutive rainfall for all cloud sizes per cell as is predicted by the Zucchini model. With small clouds, however, it can rain at the same spot several times a day, which produces more-extreme rainfall events. In this case, there are slightly more small and very large rainfall events and fewer mid-range events than in the Zucchini model.