Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.103 n.11-12 Pretoria Nov./Dec. 2007
RESEARCH LETTERS
Reliability stochastic optimization for an n-stage series system with m chance constraints
V.S.S. YadavalliI, †; A. MaladaI; V. CharlesII
IDepartment of Industrial and Systems Engineering, University of Pretoria, Pretoria 0002, South Africa
IIDepartment of Quantitative Sciences, Faculty of Business Management and Professional Studies, Management and Science University, Malaysia
ABSTRACT
This paper addresses the chance constraints reliability stochastic optimization (CCRSO) problem, for which the objective is to maximize system reliability for the given chance constraints. A method is illustrated to determine optimal solutions to an n-stage series system with m chance constraints of the redundancy allocation problem, incorporating the concepts of chance constraints techniques. One can quickly reach an exact real number solution closest to the optimal solution by this means. Once the real number solution is obtained, the branch-and-bound (B&B) technique is used to obtain the integer solution. We illustrate this approach for a 4-stage series system with two chance constraints.
Introduction
Numerous reliability optimization techniques have been proposed in the past three decades.1–4 Stochastic programming models for general redundancy-optimization problems have been studied by Zhao et al.5 Stochastic programming models arise as reformulations or extensions of reliability optimization problems with random parameters. Moreover, the resource elements vary and it is reasonable to regard them as stochastic variables. Problems in this field are not easy to solve. Most research concentrates on developing methods for approximate solutions as optimal solutions. Efficiency in the complex theoretical aspect is usually not considered. Quality statements are mostly restricted to convergence to an optimal solution without considering the implications of the running time of the algorithms for attaining the most accurate solutions. The complexity of stochastic programming problems has recently been addressed, confirming that these problems are harder than most combinatorial optimization problems. The diversity of system structures in engineering, resource constraints, and options for reliability improvement has led to the construction and analysis of several optimization models. The review by Tillman et al.1 classifies papers on reliability optimization according to system structure and its application to problem type and solution method.
This paper addresses the chance constraints reliability stochastic optimization (CCRSO) problem. The chance-constrained programming technique was first proposed by Charnes and Cooper.6 The objective is to maximize system reliability for the given chance constraints. A method is illustrated to determine optimal solutions to an n-stage series system with m chance constraints of the redundancy allocation problem. Various cases of randomness with known distributions, such as uniform, normal, and lognormal distributions, when the resource variables are random, have been discussed. Once the real number solution is obtained using the technique of chance constraints, the branch-and-bound (B&B) method is used to obtain the integer solution. We illustrate this approach for a 4-stage series system with two chance constraints.
This paper has been organized as follows: we discuss the stochastic integer programming problem for an n-stage series system with m chance constraints, and then illustrate the model by deriving the required algorithm to obtain an integer solution along with a numerical example.
Stochastic integer programming: n-stage series system with m chance constraints
The chance constraint optimization problem for an n-stage series system with m chance constraints can be formulated as

subject to P[gi(x) < bi] > 1 – αi,i = 1, 2,..., m; xj > 1, j = 1, 2,..., n, where resource vector b is random in nature; Rs is the reliability of the system; rj, qj is reliability, unreliability of components j; rj + qj ≡ 1, xj, is the number of components used at stage j; gi(x) is the chance constraint i; bi is the amount of resource i available (random), and αi is the level of significance.
Case 1. b is uniformly distributed
Let bi: U(li, ui), the constraint in system (1) is equivalent to gi(x) < τi, where 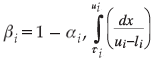 = βi, i.e. τi = αi ui + βi li.
= βi, i.e. τi = αi ui + βi li.
Hence, the deterministic equivalent of system (1) is

subject to gi(x) < αi ui + βi li,i = 1, 2,..., m; xj > 1, j = 1, 2,..., n.
Case 2. b is normally distributed
Let 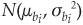 , where
, where 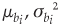 are mean and variance of the normal random variable bi. Using the ith chance constraint of the system (1), restate the chance constraint as P[bi > gi(x)] > 1 – αi,i = 1, 2,..., m, so this expression can be further stated as
are mean and variance of the normal random variable bi. Using the ith chance constraint of the system (1), restate the chance constraint as P[bi > gi(x)] > 1 – αi,i = 1, 2,..., m, so this expression can be further stated as 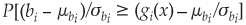 > 1 – αi,i = 1, 2..., m. Using the cumulative density function of the standard normal random 1 – Φ[(gi(x)
> 1 – αi,i = 1, 2..., m. Using the cumulative density function of the standard normal random 1 – Φ[(gi(x) 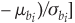 > 1 – αi,I = 1, 2,..., m, where
> 1 – αi,I = 1, 2,..., m, where 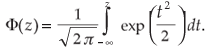 This can be further simplified as
This can be further simplified as 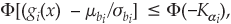 i = 1, 2,..., m. The chance constraint can be transformed into a deterministic constraint as
i = 1, 2,..., m. The chance constraint can be transformed into a deterministic constraint as 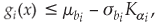 i = 1, 2,..., m.
i = 1, 2,..., m.
Hence, the deterministic equivalent of system (1) is

subject to 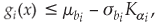 i = 1, 2..., m.
i = 1, 2..., m.
Case 3. b is log-normally distributed
Let bi: LN(µi,σi2), where µi,σi2 are mean and variance of the log-normal random variable bi. Using the ith chance constraint of system (1), we restate the chance constraint as P[ln bi > ln gi(x)] > 1 – αi,i = 1, 2, ..., m. This expression can be further stated as P[ln bi – µi)/σi > (ln gi(x) – µi)/σi] > 1 – αi,i = 1, 2,..., m. The following deterministic ith constraint is obtained by the same arguments made in case 2:
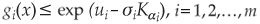
Hence, the deterministic equivalent of system (1) is:

subject to 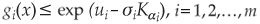 ; xj > 1, j = 1, 2,..., n.
; xj > 1, j = 1, 2,..., n.
General algorithm
1. Convert the deterministic form of the chance constraint into a linear constraint, adopting the technique of sequential linear programming.7–10
2. Code any one of the systems (2)–(4) along with their respective linearized constraints in MATLAB or LINGO and generate optimal solutions by inputting initial values using a random function (in later stages, one can use the derived real solution to generate an integer solution using the step given below).
3. Apply the branch-and-bound algorithm given below to obtain integer solutions.
Branch-and-bound technique
The B&B technique for CCRSO for stochastic optimization is as follows:
1. Solve the problem as if all the variables were real numbers, i.e. not integers, using the general algorithm given above. This solution is the upper bound (for the maximization problem) of the CCRSO problem.
2. Choose one variable at a time that has a non-integer value, say, xj, and branch that variable to the next higher integer value for one problem and to the next lower integer value for the other. The real valued solution of the variable j can be expressed as xj = [xj] + xj*, where [xj] is the integer part of xj and xj* is the fractional part of xj, 0 < xj*< 1. The lower bound and upper bound constraints of the two mutually exclusive problems are xj = [xj] and xj = [xj] + 1, respectively. Add these two constraints to both branched problems.
3. The variable xj is an integer in either branch. Fix the integer of xj for the following steps of the branch-and-bound method. Select the branch that yields the maximum objective function with all constraints satisfied. Then repeat step 2 on another variable
for each of the new sub-problems until all variables become integers.
4. Stop the particular branch if the solution does not satisfy the constraints of the original problem or else stop the branch when all the desired integer values are obtained.
Numerical example
Example 1. A four-stage system with chance constraints is formulated as a pure stochastic integer programming problem using the data given in Table 1. The decision variables, X = (x1,..., x4), are the number of redundancies at each stage. The problem is formulated as in Case 1.
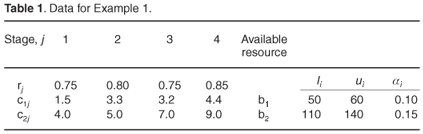
With the data given in Table 1, the real solutions are obtained using the general algorithm, which is exhibited in Table 2. We suggest that the real solution be further elaborated by the B&B technique. Let us take one solution, namely, X = (11.3697, 7.6831, 1.3097, 1.0000) from Table 2. The integer solution is obtained using the B&B technique. Figure 1 illustrates the B&B network.
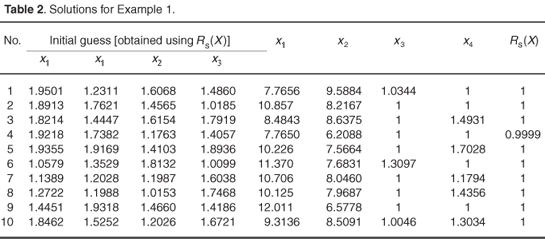
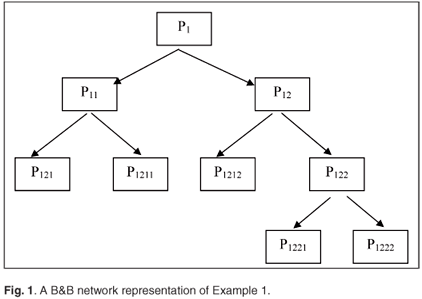
| P1 | : x1 = 11.3697; x2 = 7.6831; x3 = 1.3097; x4 = 1.0000; R = 1.0000 |
| P11 | : Fathomed |
| P12 | : x1 = 11.1175; x2 = 7.1284; x3 = 2.0000; x4 = 1.0000; R = 1.0000 |
| P121 | : x1 = 11.1175; x2 = 7.0000; x3 = 2.0000; x4 = 1.0000; R = 1.0000 |
| P122 | : x1 = 9.2000; x2 = 8.0000; x3 = 2.0000; x4 = 1.0000; R = 1.0000 |
| P1211 | : x1 = 11.0000; x2 = 7.0000; x3 = 2.0000; x4 = 1.0000; R = 1.0000 |
| P1212 | : Fathomed |
| P1221 | : x1 = 9.0000; x2 = 8.0000; x3 = 2.0000; x4 = 1.0000; R = 1.0000 |
| P1222 | : Fathomed |
An alternative optimal integer is obtained from the B&B process, X = (11, 7, 2, 1) and X = (9, 8, 2, 1).
Conclusions
The combination of the chance constraint and the B&B techniques takes advantage of an exact method and an enumerative method. In this paper the chance constraint technique, using a MATLAB program, quickly reaches real solutions that are close to optimum. In addition, the B&B technique generates many sets of integer solutions. The competitive alternatives provide management with several options and flexibility. Since a good approximation is obtained by the chance constraint technique, it does not take many branches for the B&B technique to reach the integer solution. The B&B algorithm given in this paper can be directly applied to the mixed integer stochastic programming problem (MISPP), for which only the integer variables need to be enumerated by the B&B procedure. The real variables are free of restriction after each step of the B&B technique.
1. Tillman F.A., Hwang C.L. and Kuo W. (1977). Optimization techniques for system reliability with redundancy – A review. IEEE Trans. Reliability R26, 148–155. [ Links ]
2. Tillman F.A., Hwang C.L. and Kuo W. (1980). Optimization of System Reliability. Marcel Dekker, New York. [ Links ]
3. Kuo W., Lin H-H., Xu Z. and Zhang W. (1987). Reliability optimization with the Lagrange-multiplier and branch-and-bound technique. IEEE Trans. Reliability R36(5), 624–630. [ Links ]
4. Chern M.S. (1992). On the computational complexity of reliability redundancy allocation in a series system. Operations Res. Lett. 11, 309–315. [ Links ]
5. Zhao R. and Liu B. (2003). Stochastic programming models for general redundancy – optimization problems. IEEE Trans. Reliability R52(2), 181–191. [ Links ]
6. Charnes A. and Cooper. W. W. (1954). Chance constrained programming. Management Science 6, 131–150 [ Links ]
7. Rao S.S. (2000). Engineering Optimization Theory and Practice, 3rd edn. New Age, New Delhi. [ Links ]
8. Jeeva M., Rajalakshmi R. and Charles V. (2002). Stochastic programming in manpower planning – cluster-based optimum allocation of recruitments. Advances in Stochastic Modelling. Notable Publications, New Jersey. [ Links ]
9. Jeeva M., Rajalakshmi R. Charles V. and Yadavalli V.S.S. (2004). An application of stochastic programming with Weibull distribution – Cluster based optimum allocation of recruitments in manpower planning. Stochastic Anal. Appl. 22(3), 801–812. [ Links ]
10. Charles V. and Dutta D. (2003). Bi-weighted multi-objective stochastic fractional programming problem with mixed constraints. Proc. Second National Conference on Mathematical and Computational Models. Allied Publishers, Chennai. [ Links ]
Recieved 23 November 2005. Accepted 26 March 2006.
† Author for correspondence. E-mail: sarma.yadavalli@up.ac.za














