Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.103 n.9-10 Pretoria Sep./Oct. 2007
RESEARCH LETTERS
Intensity, energy and erosivity attributes of rainstorms in the KwaZulu-Natal Drakensberg, South Africa
W. Nel*; P.D. Sumner
IDepartment of Geography and Environmental Science, University of Fort Hare, Private Bag X1314, Alice 5700, South Africa
IIDepartment of Geography, Geoinformatics and Meteorology, University of Pretoria, Pretoria 0002, South Africa
ABSTRACT
Rainfall intensity, kinetic energy and erosivity were analysed for 106 erosive storm events at five locations in the KwaZulu-Natal Drakensberg, from late 2001 to early in 2006. The stations cover an altitudinal range of 1060 m to 3165 m a.s.l. and provide the first detailed rainstorm data for the Drakensberg area. Erosive storm events, defined as total rainfall exceeding 12.5 mm and a maximum 5-minute intensity greater than 25 mm h–1, are found to vary in duration and depth (total rainfall) with the distribution biased towards shorter, shallower storms. Erosive rainstorms are almost exclusively a summer phenomenon and the attributes of these storms (rainfall intensity, kinetic energy and erosivity) are positively correlated with rainfall depth, but not with storm duration. Inter-station similarities exist with respect to rainfall depths and mean kinetic energy from individual storm events. Altitudinal trends are, however, evident for storm maximum intensity, depths of erosive storms and cumulative kinetic energy. Together with frequency of erosive events and extent of collective erosive effects, all these rainfall attributes decrease with station altitude. Dissimilarities in cumulative kinetic energy and cumulative erosivity can be explained by the lack of erosive events during early and late summer on the escarpment and by significant erosive rains during this period at lower altitudes in the foothills.
Introduction
South Africa is predominantly a semi-arid country and it is only primarily in the east that areas record rainfall above 600 mm per annum.1 Along the KwaZulu-Natal Drakensberg escarpment, annual rainfall has been estimated to exceed 1500 mm, although recent records show that this could be an overestimate.2 The escarpment typically reaches above 2800–3000 m in altitude and defines the watershed between the interior catchments of Lesotho, and the shorter and steeper catchments of KwaZulu-Natal (Fig. 1). KwaZulu-Natal contributes nearly twice as much runoff per unit of rainfall as South Africa as a whole, and a quarter of South Africa's streamflow.3 Rainfall in the Drakensberg is highly seasonal, with the five summer months (November to March) accounting for 75% of the annual total, whereas winter months (May to August) contribute less than 10%.4 The main source of precipitation is large-scale line thunderstorms and orographically induced storms that develop mostly over the extended summer period.5 During winter, cold fronts affect KwaZulu-Natal, bringing occasional rain and snowfalls to the mountains.5 Snowfalls are thought to contribute around 100 mm water equivalent to precipitation totals,2 or less than 10% of the rainfall total, but the exact contribution remains unmeasured.
Rainfall erosivity is a major driving force of many hydrological and erosional processes6 and the amount of soil that is detached, as well as other key processes in water erosion, is related to rainfall intensity.7 A combination of rainfall intensity and raindrop fall velocity influences soil splash rate,8 while the extent of erosion caused by rainfall in a storm depends on the rainfall's physical characteristics, including intensity, amount, drop-size distribution, terminal fall velocity, wind speed and inclination.9 Rainfall kinetic energy in particular has been suggested to influence sediment transport10 as well as to act as an indicator of erosivity,11,12 and is used in soil erosion modelling.13 Rainfall intensity can be measured directly, but measurements of kinetic energy and raindrop sizes are, in most cases, unavailable; hence the empirical relationships between rain intensity and kinetic energy.14
Few studies have investigated contemporary rainfall erosivity in the KwaZulu-Natal mountains. Schulze1undertook a study of rainfall kinetic energy using two stations in the central Drakensberg; Cathedral Peak at 1854 m and Ntabamhlope Research Station at 1457 m a.s.l. More recently, in an investigation of rainfall erosivity in southern Africa, Seuffert et al.15 used one station in the central Drakensberg foothills as representative of the mountainous area. Given the paucity of existing data, the aim of the study reported here was to investigate storm erosivity in the summit area and in the foothills east of the escarpment. First, we analysed the characteristics of individual rainstorms. Second, rainfall intensity and kinetic energies of storm events were examined; and finally, rainfall frequency and the magnitude of storm erosivity were determined.
Study sites and data collection
Davis-MC Systems (D-MCS) automated tipping-bucket rain gauges were installed at five Drakensberg locations. These gauges have a 163 mm collection diameter and log totals every 5 min on a tipping resolution of 0.2 mm rainfall. Two sites are on the escarpment edge; one at the summit of Sani Pass (2850 m a.s.l.) in what is known as the southern Drakensberg, and another on the Sentinel Peak (3165 m) in the northern Drakensberg. Gauges were also installed below the escarpment at the Injisuthi Outpost (1920 m) and on the farm Glenisla (1060 m), both in the central Drakensberg, and in Royal Natal National Park (RNNP) (1392 m) in the north (Fig. 1). The two high-altitude stations are the first that attempt to record detailed and long-term rainfall data from the upper reaches of the catchments.
Rainfall at the top of Sani Pass was monitored from September 2001 until mid-April 2003. Some data were thereafter lost due to wind damage, but the logger ran again from early September 2003 to early January 2006, thus including a total of 1425 record-days. Monitoring on the summit of Sentinel Peak began in late November 2002 and data here are for 1201 days, from November 2002 to March 2006. At RNNP, rainfall records began in November 2001 and ended in January 2005 (1147 days). Data presented here for the Injisuthi Outpost are from October 2001 to January 2004 (828 days) and at Glenisla from October 2001 to April 2003 (528 days).
Data analysis and results
Stocking and Elwell16 classify a distinct erosive rainfall event as a storm when total rainfall exceeds 12.5 mm, maximum 5-minute intensity exceeds 25 mm h–1 and the event is isolated by at least a rain-free two-hour period. Applying this definition, the data from the five gauge locations include 106 erosive storm events.
Storm characteristics
Of the 106 storm events, 49 storms were measured at the RNNP station. At Glenisla farm 23 storms were recorded, 14 at Injisuthi Outpost, and at Sani Pass and at Sentinel Peak 9 and 11 storms, respectively. The shortest erosive storm lasted 20 minutes and the longest 26 hours. These storms had a mean duration of 279 minutes (4 hours and 36 min) but the distribution is noticeably skewed (CV = 1.0), with 25% of the storms being shorter than 106 minutes (1 hour and 46 min) and 75% shorter than 335 minutes (5 hours and 36 min). Mean depth (total rainfall) of all individual storm events was 25.3 mm, with the lowest totalling 12.6 mm and the highest 72.0 mm. This distribution is also skewed (CV = 0.5), with 25% of all storms having a rainfall depth of between 12.6 and 15.7 mm, 75% less than 29.5 mm, and 90% of all storms a depth of less than 47.3 mm. There is a statistically significant (P < 0.001) positive correlation (R = 0.61) between storm depth and storm duration.
Given the expected seasonality of rainfall in the Drakensberg,4 monthly rainfall at each station was compared with monthly erosive rainfall (Fig. 2). At the RNNP and Glenisla stations, approximately 40% of the total rainfall measured originates from erosive rainfall events. The high-altitude stations of Sani Pass and Sentinel Peak measured the least rainfall from erosive events, at 8% and 12% of total rainfall, respectively. No erosive storms were recorded during the months of May, June, July and September (Fig. 2), even though collectively 907.4 mm of rainfall was measured at the sites during these months. Glenisla and Sentinel Peak each recorded one erosive event during August, and all other erosive events occurred from October to April, with the highest number logged during January.
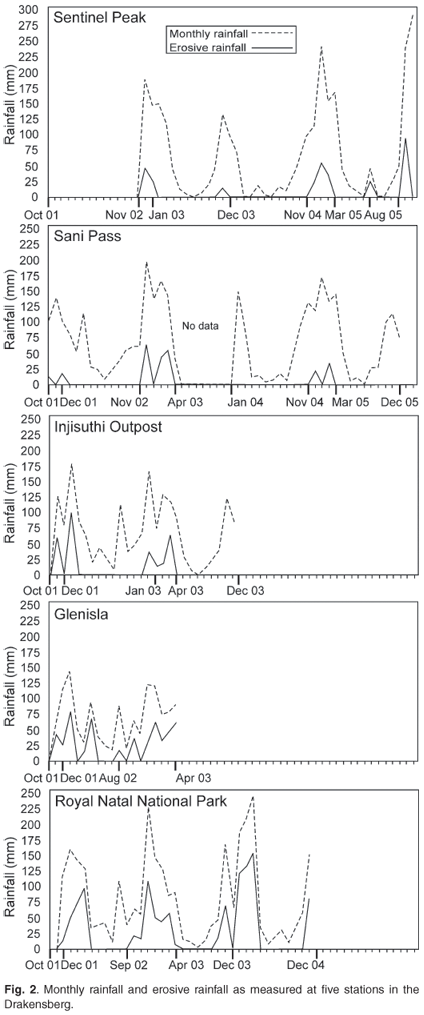
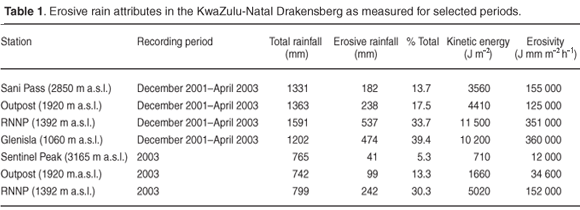
Differences in the distribution and magnitude of monthly erosivity are evident from measurements during 2003 at the RNNP, Sentinel Peak and Injisuthi Outpost stations (Table 1). Although erosive rain was only recorded in summer, there were inter-station differences in the intra-annual distribution of erosive rainstorms. During the early and late summer months of 2003 (February, March and October) no erosive rainfall was recorded at the Sentinel, while at Injisuthi Outpost 30% and at RNNP 45% of total rainfall was erosive. From the 17 months of 5-minute rainfall data from December 2001 to April 2003 at Sani Pass, Glenisla, Injisuthi Outpost and RNNP (Table 1), an altitudinal difference is apparent in the amount of rainfall from erosive storms as a percentage of total rainfall. The lowest station, Glenisla, recorded 39% of its total rainfall from erosive events. At RNNP, 34% was erosive; while at Injisuthi Outpost 18% and at Sani Pass, the highest station, only 14% of total rainfall was generated by erosive events. The foremost difference between stations is that those at higher altitude (Injisuthi Outpost and Sani Pass) recorded no erosive rainfall during the early and late summer months (March, April and October) of 2002, while the lower altitude stations recorded substantial erosive rainstorms during the same period (Fig. 2).
Rainfall intensity
Five-minute rainfall intensity (I5) of erosive events measured at the different stations ranged from 26.4 to 144 mm h–1 and 30-minute rainfall intensity (I30) ranged from 8.0 to 70.4 mm h–1. The maximum rainfall intensity of 144 mm h–1 was measured at the lowest station Glenisla (Table 2). At RNNP, 120 mm h–1 was recorded, and at Injisuthi Outpost, Sani Pass and Sentinel Peak (the highest station) the maximum I5 values measured were 93.6, 79.2 and 69.6 mm h–1, respectively (Table 2). Altitude appears to influence maximum 5-min intensities, but mean 5-min and 30-min rainfall intensities at the different locations for individual events show no appreciable differences (Table 2). There is a statistically significant, positive correlation between storm depth and maximum 5-min intensity (R = 0.25, P = 0.01) and storm depth and maximum 30-min intensity (R = 0.54, P < 0.001) but no statistically significant correlation between mean storm intensity and storm depth.
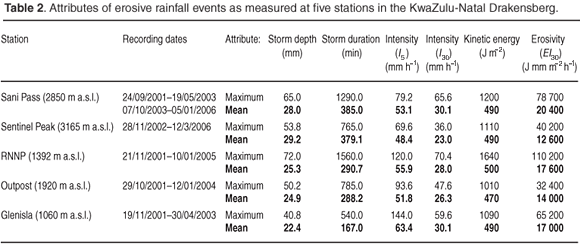
We also considered the occurrence of high-intensity storms; those exceeding an I5 of 50 mm h–1.17 RNNP had 27 such events during the recording period, Injisuthi Outpost experienced only 7, and Glenisla 14. The high-altitude stations (Sani Pass and Sentinel Peak) had the fewest events, with 5 and 6 recorded, respectively.
Storm kinetic energies
Wischmeier and Smith18 used measurements of drop size and terminal velocity to derive a relationship between rainfall intensity and kinetic energy. The proposed relationship is a logarithmic function of the form

where the intensity R is in mm h–1. Van Dijk et al.7 critically appraised the literature on the rainfall intensity–kinetic energy (R–EK) relationship and, based on the average parameter values that were derived from the best available data, the general equation to predict storm kinetic energy content from rainfall intensity data is
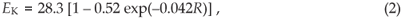
where R is again rainfall intensity. Earlier work by Elwell and Stocking19 in Zimbabwe, however, shows that in subtropical climates the kinetic energy of rainfall (in J m–2 mm–1) is predicted by the equation

where the intensity I is in mm h–1. This equation has also been adopted for use in the Soil Loss Estimation Model for Southern Africa (SLEMSA) and was applied by Schulze20 in a first assessment of the kinetic energy of rainfall in South Africa. For the purpose of a spatial study, and in order to allow for consistency with previous studies in southern Africa, the equation by Elwell and Stocking19 [Equation (3)] is used here to assess the 5-min incremental kinetic energy content. A uniform drop-size distribution is assumed in analysis of kinetic energy. Total storm kinetic energy (E) generated during each individual erosive storm event is calculated through the 5-min kinetic energy content, multiplied by the quantity of rain (mm) falling in that period, to derive the 5-min kinetic energy. Each of these values generated during the storm is then summed to give the total storm kinetic energy.
Maximum energy produced during any individual storm was 1640 J m–2, recorded at RNNP; the storm with the lowest kinetic energy was also measured at this station (140 J m–2). Mean kinetic energy of all erosive events was 490 J m–2 with no large difference between stations (Table 2). An altitudinal difference is apparent with respect to cumulative energies on the overlapping period December 2001 to April 2003 (Table 1). Kinetic energies measured at the Glenisla and RNNP stations are 10 200 J m–2 and 11 500 J m–2, respectively. Lower kinetic energy totals were measured at the higher altitude stations of Injisuthi Outpost (4410 J m–2) and lower again at the escarpment station Sani Pass (3560 J m–2). Similarly, during 2003 at RNNP the annual kinetic energy generated by erosive events was 5020 J m–2, with the corresponding values for Injisuthi Outpost and Sentinel Peak being 1660 J m–2 and 710 J m–2, respectively (Table 1). A strong, statistically significant correlation was found between storm kinetic energy and storm depth (R = 0.83; P < 0.001); however, there was no correlation between storm kinetic energy and storm duration.
Storm erosivity
Seuffert et al.15 developed an integrated rainfall erosivity index (REI) for assessing rainfall structure, runoff and erosion from several factors including rainfall quantity, energy, (dis)continuity, intensity and spatial pattern. Soil erosion can also be measured through process-based models such as the Water Erosion Prediction Project (WEPP),21 where inter-rill erosion or detachment (Di) is modelled as a function of the effective rainfall intensity (Ie). The European Soil Erosion Model (EUROSEM)13 predicts soil detachment by raindrop impact (DR) as a function of total kinetic energy (KE). Erosivity can also be determined by the product (EI30) of the total kinetic energy (E) of the storm and its maximum 30-min intensity (I30), developed by Wischmeier and Smith.22 This equation has been used globally as part of the (Revised) Universal Soil Loss Equation, has been applied in southern Africa to asses the spatial distribution of erosivity,16,23,24 and reflects the combined potential of raindrop impact and turbulence created in overland flow. To be consistent with erosivity studies in southern Africa, the spatial distribution of erosivity in our work was determined by the value of EI30 for each individual storm.
Storm EI30 values vary considerably in the Drakensberg, with the maximum erosive power generated by a storm being 110 000 Jmmm–2 h–1 and a minimum erosivity of 1140 J mm m–2 h–1, both recorded at RNNP. Mean erosivity of storm events for all stations is 16 300 J mm m–2 h–1 and differences exist between stations regarding the mean storm erosivity generated during individual events (Table 2). As with kinetic energy, cumulative erosivity also differs between stations. Erosiviies measured at Glenisla and RNNP from December 2001 to April 2003 (Table 1) were 360 000 and 351 000 J mm m–2 h–1, respectively, but at the higher altitude stations of Injisuthi Outpost (125 000 J mm m–2 h–1) and Sani Pass (155 000 J mm m–2 h–1) values were lower than at the low-altitude stations. At RNNP the annual erosivity generated by erosive events was 152 000 J mm m–2 h–1 in 2003, but at Injisuthi Outpost (34 600 J mm m–2 h–1) and on the escarpment at Sentinel Peak (12 000 J mm m–2 h–1) the corresponding values were an order of magnitude lower. Storm erosivity was also investigated in relation to storm depth and duration. Similar to storm kinetic energy, there was a significant correlation (R = 0.72; P < 0.001) between storm erosivity and depth, but no correlation between erosivity and duration.
Discussion
Erosive storm events across the KwaZulu-Natal Drakensberg vary considerably in duration as well as in depth, and the distribution of events is skewed with a bias towards shorter, shallower storms. Rainfall is expected to be highly seasonal4 and this pattern is also observed in the occurrence of erosive storms with none recorded during the winter months of May, June and July, and only two such events during August. There appears to be a clear contrast between the kinetic energy of orographic storms and those associated with drizzle.7 In South Africa, there is a strong correlation between high-intensity rainfall and thunderstorm activity; low-intensity rainfall is normally associated with frontal systems.20 In the Drakensberg, rainfall in winter displays much lower kinetic energy than in mid-summer;17 an apparent seasonality of erosive events should thus be related to the source of precipitation. The findings indicate that frontal rainfall during winter gives rise to non-erosive, low-intensity drizzle, whereas erosive events that are primarily a summer phenomenon are linked to thunderstorms.
Tyson et al.5 indicate that mean annual rainfall increases with altitude, and that the corresponding value for the top of the escarpment should be over 2000 mm. Schulze1 also defined a clear relationship between altitude and rainfall, and predicted mean annual rainfall exceeding 1800 mm and a January rainfall of 250 mm along the escarpment, but these estimates have been challenged.2,25 There is a significant linear relationship between mean annual rainfall and altitude below 2100 m a.s.l.,4 but whether the increase in rainfall with altitude extends up to the escarpment (above 2100 m a.s.l.) is uncertain. Rainfall totals measured at the different stations for the same period, as well as mean kinetic energies from individual storm events show no spatial difference. Depth of erosive storms as well as cumulative kinetic energy and erosivity do, however, depend on altitude. A high proportion of rain falls as erosive events at the lower altitude stations and only a correspondingly small percentage at the escarpment edge. The lower altitude stations record higher maximum intensities, cumulative kinetic energies and erosivities than those at higher altitude. The main difference can be attributed to lower altitude stations recording considerable erosive rains during the early and late summer, whereas at higher altitude no erosive events were recorded during that period.
Raindrop size distribution at a given intensity should decrease with altitude,7 although greater fall velocities associated with higher elevations could offset the effect on kinetic energy.26 In the central Drakensberg, Schulze1 reported a greater frequency of high intensity storms at Ntabamhlope (1457 m a.s.l) than at the more elevated Cathedral Peak (1854 m a.s.l). Ntabamhlope also showed higher annual kinetic energy at Cathedral Peak per unit of rainfall.1 Seuffert et al. (Fig. 8, ref. 15) suggest that in the Drakensberg the rainfall erosivity index decreases from east to west from the foothills to the escarpment. Similarly, our study found that a lower percentage of rain falls at higher altitude stations as erosive storms, and that the erosivity of rainfall decreases up the escarpment.
Conclusion
Erosive storm events across the KwaZulu-Natal Drakensberg vary in duration and depth, but tend to be short and shallow. Erosive rainfall is associated with thunderstorms and is highly seasonal, with few erosive storms occurring at the study sites during winter. Storms with higher rainfall totals tend to have higher maximum rainfall intensities, kinetic energies and erosivity. The proposed increase in rainfall with altitude in the Drakensberg1,5 is not apparent in our data that compare rainfall totals measured at different stations for the same period.
This study found that an increase in altitude in the Drakensberg is associated with reduced maximum rainfall intensity of erosive events. High-altitude stations recorded lower maximum 5-min rainfall intensities and fewer high intensity events than those at lower altitude, but mean kinetic energy produced during individual storms was similar throughout the area. Individual storm events at all altitudes in the Drakensberg therefore have the potential to detach soil, but at high altitude a lower percentage of rain falls as erosive storms, and the cumulative kinetic energy produced as well as total erosivity of rainfall is less on the escarpment than at lower altitudes. This conclusion compares well with earlier findings from two stations in the foothills1 and with the REI estimates by Seuffert et al.15 Altitudinal differences in cumulative kinetic energy and cumulative erosivity can be explained by the lack of erosive rainstorms during early and late summer at the escarpment, and significant erosive rains during this period at lower altitudes in the foothills.
The Department of Geography, Geoinformatics and Meteorology at the University of Pretoria supplied equipment and principal funding. The Govan Mbeki Research and Development Centre at the University of Fort Hare provided additional funding.
1. Schulze R.E. (1979). Hydrology and Water Resources of the Drakensberg. Natal Town and Regional Planning Commission, Pietermaritzburg. [ Links ]
2. Nel W. and Sumner P.D. (2005). First rainfall data from the KZN Drakensberg escarpment edge (2002 and 2003). Water SA 31, 399–402. [ Links ]
3. Whitmore J.S. (1970). The hydrology of Natal. Paper No. 1, 2nd Technical Session, Symposium Water Natal, Durban. [ Links ]
4. Nel W. and Sumner P.D. (2006). Trends in rainfall total and variability (1970–2000) along the KwaZulu-Natal Drakensberg foothills. S. Afr. Geog. J. 88, 130–137. [ Links ]
5. Tyson P.D., Preston-Whyte R.A. and Schulze R.E. (1976). The Climate of the Drakensberg. Natal Town and Regional Planning Commission, Pietermaritzburg. [ Links ]
6. Moore T.R. (1979). Rainfall erosivity in East Africa. Geogr. Ann. 61A, 147–156. [ Links ]
7. Van Dijk A., Bruijnzeel L. and Rosewell C. (2002). Rainfall intensity–kinetic energy relationships: a critical literature appraisal. J. Hydrol. 261, 1–23. [ Links ]
8. Ellison W.D. (1944). Studies of raindrop erosion. Agric. Engng 25, 131–136. [ Links ]
9. Obi M.E. and Salako F.K. (1995). Rainfall parameters influencing erosivity in southeastern Nigeria. Catena 24, 275–287. [ Links ]
10. Hudson N.W. (1965). The influence of rainfall on the mechanics of soil erosion with particular reference to southern Rhodesia. M.Sc. thesis, University of Cape Town, South Africa. [ Links ]
11. Free F. (1960). Erosion characteristics of rainfall. Agric. Engng 41, 447–449. [ Links ]
12. Ghadiri H. and Payne D. (1977). Raindrop impact stress and the breakdown of soil crumbs. J. Soil Sci. 28, 247–258. [ Links ]
13. Morgan R.P.C., Quinton J.N., Smith R.E., Govers G., Poesen J.W.A., Auerswald K., Chisci G., Torri D. and Styczen M.E. (1998). The European Soil Erosion Model (EUROSEM): a dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf. Proc. Landf. 23, 527–544. [ Links ]
14. Nyssen J., Vandenreyken H., Poesen J., Moeyersons J., Deckers J., Haile M., Salles C. and Goyers G. (2005). Rainfall erosivity and variability in the Northern Ethiopian Highlands. J. Hydrol. 311, 172–187. [ Links ]
15. Seuffert O., Herrig K., Ollesh G. and Busche D. (1999). REI: an integrated rainfall erosivity index for assessing and correlating rainfall structure, runoff and erosion. Geoökodynamik 20, 1–54. [ Links ]
16. Stocking M.A. and Elwell H.A. (1976). Rainfall erosivity over Rhodesia. Inst. Br. Geog. Trans. 1, 231–245. [ Links ]
17. Schulze R.E. (1978). Rainfall intensities, kinetic energies and probabilities: examples of applied climatological studies of Natal. Water SA 4, 179–191. [ Links ]
18. Wischmeier W.H. and Smith D.D. (1958). Rainfall energy and its relation to soil loss. Trans. Am. Geophys. Un. 39, 285–291. [ Links ]
19. Elwell H.A. and Stocking M.A. (1973). Rainfall parameters for soil loss estimation in a subtropical climate. J. Agric. Engng Res. 18, 169–177. [ Links ]
20. Schulze R.E. (1980). The distribution of kinetic energy of rainfall in South Africa—A first assessment. Water SA 6, 49–58. [ Links ]
21. Nearing M.A., Foster G.R., Lane L.J. and Fincker S.C. (1989). A process-based soil erosion model for USDA-Water Erosion Prediction Project technology. Trans. ASAE 32, 1587–1593. [ Links ]
22. Wischmeier W.H. and Smith D.D. (1978). Predicting Rainfall Erosion Losses. Agricultural Handbook 537, USDA, Washington, D.C. [ Links ]
23. Smithen A.A. (1981). Characteristics of rainfall erosivity in South Africa. M.Sc. thesis, University of Natal, Pietermaritzburg. [ Links ]
24. Smith H.J., Van Zyl A.J., Claassens A.S., Schoeman J.L. and Laker M.C. (2000). Soil loss modelling in the Lesotho Highlands Water Project catchment area. S. Afr. Geog. J. 82, 64–69. [ Links ]
25. Nel W. and Sumner P.D. (in press). Rainfall and temperature attributes on the Lesotho-Drakensberg escarpment edge, southern Africa. Geogr. Ann. A 90(1). [ Links ]
26. Beard K.V. (1977). Terminal velocity adjustment for cloud and precipitation drops aloft. J. Atmos. Sci. 34, 1293–1298. [ Links ]
Received 29 June. Accepted 15 September 2007.
* Author for correspondence. E-mail: wnel@ufh.ac.za














