Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Journal of the Southern African Institute of Mining and Metallurgy
On-line version ISSN 2411-9717
Print version ISSN 2225-6253
J. S. Afr. Inst. Min. Metall. vol.117 n.5 Johannesburg May. 2017
http://dx.doi.org/10.17159/2411-9717/2017/v117n5a13
PAPERS OF GENERAL INTEREST
The use of fuzzy-weighted binary integer goal programming to select the optimum site for a central processing plant
E. Bakhtavar; D. Khademi; R. Mikaeil
Department of Mining and Material Engineering, Urmia University of Technology, Urmia, Iran
SYNOPSIS
Fuzzy-weighted integer goal programming has been developed and used to select the most suitable site to construct a central processing plant for several adjacent small-scale dimension stone quarries, based on the most effective criteria. In the first step of mathematical modelling, the most important goals and decision variables were defined. Accordingly, an objective function was used in the model for minimizing the sum of undesired fuzzy-weighted deviations. Fuzzy weights were determined by a matrix of pairwise comparisons of various expert judgments in this field and the fuzzy geometric mean. The goal and systemic constraints were also modelled. The most suitable site for the construction of the plant was selected after solving the mathematical model in the Excel® Solver add-in. The selected site had various advantages over the other sites, such as the shortest average distance to the quarries, the shortest distance to power access and workforce, and the lowest land price.
Keywords: uzzy multi-objective, goal programming, binary integer, dimension stone quarry, processing plant.
Introduction
Selection of the most suitable site of a plant is one of the most important considerations when constructing an industrial project. A suitable site has a significant effect on a company's competitiveness in the market. Selecting a desirable location for constructing plants such as mineral processing facilities is an essential part of the economic planning that will enable a company to meet the needs of related upstream and downstream operations. These units are considered to be best built near the relevant mining sites because of technical difficulties, the cost of transporting minerals, and the traffic hazard caused by the movement of trucks transporting materials. Two main types of research using multiattribute decision-making models have been reported for selection of a processing plant site (Safari et al. 2010, 2012). In that research, the analytic hierarchy process (AHP) and fuzzy technique for order preference by similarity to ideal solution (TOPSIS) approach were applied to select the suitable locations for the mineral processing plants for phases 1 and 2 of Sangan iron ore mine.
Fuzzy goal programming has been developed to solve decision-making problems in a variety of specific scientific applications. However, this technique has not been applied to date for processing plant site selection. A vendor selection decision in a supply chain was formulated as a fuzzy mixed integer goal programming by Kumar, Vrat, and Shankar (2004). A fuzzy multi-goal programming model was developed to select 'thin film transistor liquid crystal display suppliers for cooperation' (Lee, Kang, and Chang, 2009). A fuzzy AHP approach was used to analyse the importance of effective factors based on experts' judgment. Arikan (2013) developed a multi-objective linear programming method to select a multi-source supplier. The programming approach was based on a fuzzy mathematical model and a specific solution using the decision-maker's aspirations for fuzzy goals. Jadidi, Cavalieri, and Zolfaghari (2015) proposed a multi-choice goal programming approach to solve a supplier selection problem, taking into consideration the preferences of decision-makers. Jinturkar and Deshmukh (2011) developed a fuzzy mixed integer goal programming model to plan rural energy for domestic use. Izadikhah (2015) introduced a fuzzy goal programming approach to select a practical machine tool for a manufacturing company. Jones and Wall (2015) developed an extended goal programming model to select an offshore wind farm site in the UK, using a parametric analysis at a meta-objective level.
The most important aspects specific to the current investigation, which have not been considered in other research related to site selection for a processing plant, are as follows:
► Consideration of several small-scale quarries (mines) that are adjacent to each other rather than selection for a processing plant site for one particular mine
► Selection of a site for a dimension stone processing plant. The decision-making process for selecting a plant site for a dimension stone quarry are completely different from those for a metal mine
► A multi-objective mathematical goal programming model with fuzzy weights was developed in the objective function and binary integer decision variables.
Due to the large number of dimension stone quarries in the West Azerbaijan province of Iran and their importance, there is a need to solve a more complex problem. This paper proposes an integrated multi-attribute and multi-objective model to select the most suitable site for a processing plant in all cases where there are several adjacent small-scale dimension stone quarries.
Material and methods
Selection of the most suitable site to construct a processing plant for several adjacent dimensional small-scale stone quarries has a multi-objective nature, and as such, goal programming is used for base modelling. Also, the objective here is to select one alternative among others, indicating the necessity of using (0-1) binary integer variables, in which the value of 'one' signifies selection of an alternative, and 'zero' signifies rejection. Each of the criteria (goals) has different importance, so each should be assigned a different weight. The following criteria are considered in order to identify the most suitable site for construction of a dimensional stone processing plant:
► Depth of groundwater
► Distance to high-voltage power source
► Distance to urban gas supply
► Average distance of the quarries from the alternative plant sites
► Distance to the point of consumption and processed stone markets
► Closest distance to local labour
► Topography
► Land price.
The fuzzy-weighted geometric mean of pairwise comparisons from different experts can be used to apply real conditions that are often uncertain and fuzzy in nature. Hence, the proposed approach is termedfuzzy-weighted binary integer goal programming and is, in fact, a developed version of the goal programming model. Firstly, we examine the steps and nature of the proposed approach, using a mining region that includes four small-scale travertine dimension stone quarries. The most important criteria and related effective goals on theoretical problem-solving are then expressed. In the next step, taking into account the degree of importance and the effectiveness of each goal in selecting the most desired alternative, the method of the fuzzy-weighted geometric mean from pairwise comparisons from different experts is used. After defining both types of systemic and goal variables, the fuzzy objective function and the related constraints are modelled mathematically.
Studied sites and quarries
Three sites were pre-selected for the study to find the most suitable site for a plant to process the stone extracted from four adjacent small-scale travertine quarries within the city limits of Takab, located in Western Iran. The names of the quarries and the distance of each from the studied sites are listed in Table I.
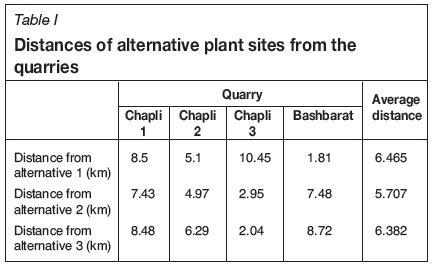
The first alternative plant site is near the village of Bashbarat and the road of Shahindezh-Takab in close proximity to the city of Takab. The second alternative is located about 2 km from the village of Chapli towards Shahindezh. The third alternative is located about 3 km from the village of Chapli towards Shahindezh. Photographs of the quarries are given in Figure 1.

Goals
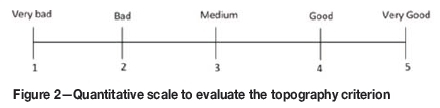
Table II summarizes the most important criteria and the related data based on the three considered alternatives. The topography criterion is initially evaluated by a qualitative scale, then by using the quantitative scale shown in Figure 2.
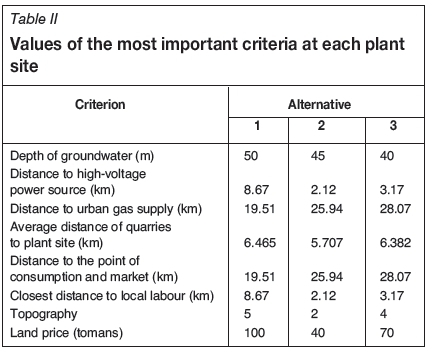
According to the criteria in Table II, the goals considered in the case study are as follows:
► Goal 1: Maximum distance between the plant site and the quarries. The maximum distance for the case study is 5 km
► Goal 2: Maximum distance between the plant site and the point of consumption (sales market). The maximum distance for the case study is 20 km
► Goal 3: Maximum distance between the plant site and high-voltage power source. The maximum distance for the case study is 1 km
► Goal 4: Maximum distance between the plant site and the workforce. This maximum distance for the case study is 4 km
► Goal 5: Maximum depth to access groundwater. In the study region, the cost of drilling is approximately doubled at depths of over 45 m. Therefore, the maximum depth is considered to be 45 m
► Goal 6: According the classification for topography (Figure 2), the desirable topography is in the category 'good'
► Goal 7: A maximum cost should be assigned to acquiring the land for the plant site. Regarding the initial investment limitation and conditions in the region, the maximum land price is 70 million tomans ($21 000)
► Goal 8: Maximum distance between the plant site and gas supply. This maximum distance for the case study is 10 km.
Determining weights forgoals
First, a qualitative questionnaire was prepared and completed by 12 experts in the field to determine the weights of the goals. Pairwise comparison matrices composed of triangular fuzzy numbers are formed using information collected from the completed questionnaires and regarding a common fuzzy scale. An example of a fuzzy triangular pairwise comparison matrix resulting from the judgments of experts is given in Table III.
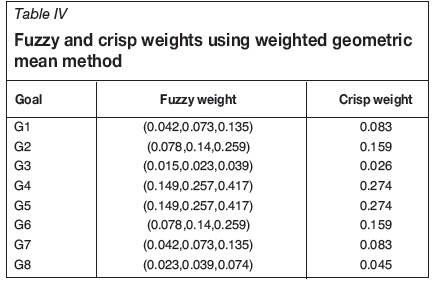
In the next step, the weighted geometric mean method, which was introduced by Aczel and Saaty (1983) as the best method for the aggregation of individual judgments, is developed to apply in the fuzzy form according to Equations [1] and [2]. Each goal's fuzzy weight is determined using Equations [1] to [3]. First, the fuzzy triangular geometric mean weight of criterion (goal) i in comparison with criterion j based on the judgments by all experts is determined using Equation [1]. Then, Equations [2] and [3] are used to determine the fuzzy triangular geometric weight of each goal. Finally, the fuzzy triangular geometric weights are defuzzified using Equation [4] as the centre of area defuzzification method to obtain crisp weights; the results are given in Table IV.
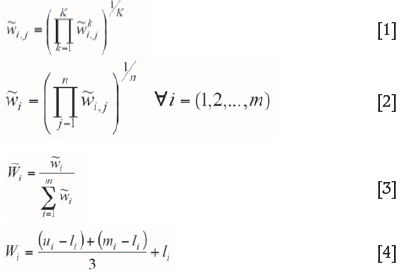
where
is the fuzzy triangular geometric mean weight of criterion (goal) i in comparison with j based on the judgments by all experts
is the fuzzy triangular weight of criterion (goal)i in comparison with j based on the judgment of Mi expert
K is the number of experts is the fuzzy triangular geometric mean weight of ith goal
is the fuzzy triangular geometric weight of ith goal; it is defined as (lv mo ui)
is the crisp weight of ith goal
lj is the lower point of the fuzzy triangular weight of ith goal
mi is the middle point of the fuzzy triangular weight of ith goal
ui is the upper point of the fuzzy triangular weight of ith goal
Definition ofsystemic and goal decision variables
The first step of mathematical modelling and formulating a mathematical model is to define the decision variables that form the base of the mathematical programming. The nature of programming for this investigation is a little different because it is multi-objective and based on goal binary intege programming, in that a series of goal variables should be defined in addition to systemic decision variables, which in fact indicate amounts of desirable and undesirable deviations from the goals. Goal variables (desirable and undesirable deviations where i is an index for the goals), unlike systemic variables (χ, wherej is the index for the alternatives) that have the nature of zero and unity are both in the objective function and the constraints. In fact, the objective function is only based on goal variables (undesirable deviations) and goal constraints are modelled using all systemic and goal variables. Systemic and goal variables used in this case study are as follows:
where i is an index for the goals), unlike systemic variables (χ, wherej is the index for the alternatives) that have the nature of zero and unity are both in the objective function and the constraints. In fact, the objective function is only based on goal variables (undesirable deviations) and goal constraints are modelled using all systemic and goal variables. Systemic and goal variables used in this case study are as follows:
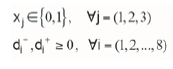
Definition of the objective function and constraints
The general mathematical expression of the objective function in the developed approach is according to Equation [5]. It indicates minimization of the sum of undesirable deviations from different goals by considering the degree of importance and affecting the weight of each. The objective function is modelled as Equation [6] by considering the effec of the fuzzy weights for each of the goals. The goal constraints are expressed as Equations [8] to [15] based on Equation [7] and using the data summarized in Table II. The only systemic constraint is modelled as Equation [16].
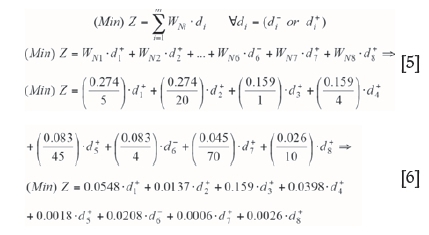

Results and discussion
In this section, the model formulated as Equations [5] to [16] is used to select the most suitable processing plant site from the three pre-selected sites. The model was solved using Excel® Solver on a computer with a 2.4 GHz processor and 4 GB RAM. The results, including both deviational and systemic decision variables as well as achievement values of goals, are presented in Table V.
According to the results given in Table V and the software output (Figure 3), the second alternative is the most suitable site. The second site is closer to the quarries, the high-voltage power source, and workforce, although it has only a moderate access level to groundwater and a moderate distance to the market and gas supply. Furthermore, it is more desirable than other sites on the basis of topography and land price. The first alternative (site) is well positioned in terms of distance to the market and gas supply, but in other aspects it is less desirable. The third alternative has only the best access to water.
The resulting deviational values for the four goals 1, 2, 3, and 8 are 0.7, 5.9, 1.1, and 15.9, respectively. However, other deviational values for goals 4, 5, 6, and 7 were zero. It is worth noting that only undesirable goal variables 1, 2, 3, and 8 influence the total value of the objective function (0.3393). As observed, goals 4, 5, 6, and 7 are satisfied by the exact upper bound values of 4, 45, 4, and 70, respectively; without any deviation. On the other hand, goals 1, 2, 3, and 8 have been satisfied through the values 5.03836, 20.08083, 1.1749, and 10.4134, respectively after adding deviational values (0.03836, 0.08083, 0.1749, and 0.4134) to their upper bounds. The third goal constraint includes a higher deviation than other goal constraints. According to goal constraint 8, access to gas supply includes an additional cost. Goal constraint 1, with a very low deviation, reveals that if the distance of the quarries from a given plant site is less and connection is possible in all seasons of the year, it could be considered as effective regarding the supply of raw materials. Goal constraint 2 includes a negligible deviation. Based on that, being near to the point of consumption (market) is one of the most important parameters for a construction site.
Other goal constraints (4, 5, 6, and 7) have no deviation. In this case, based on goal constraint 4, many personnel are indoors workers and less experienced people, and for this reason, the maximum distance to a workforce is 4 km, with no deviation value. One of the basic requirements for a stone cutting and processing plant is a plentiful water supply to cool the cutting and polishing machinery. Water wells are usually used for this purpose. According to goal constraint 5, the best location for the plant will be where the groundwater is closest to the surface, where minimum drilling will be required to access the water. The maximum drilling depth is 45 m with no deviation value, and the cost of drilling doubles at greater depths. As goal constraint 6 is defined, in areas with flatter topography less excavation is required, and there is more flexibility in the location and extent of activities. As considered in goal constraint 7, the price of land is an important parameter. However, this is a one-time payment, so the maximum price is considered as being 70 million tomans ($21000) without any deviation.
Considering the in-situ investigations in the studied area and based on the priorities of the related goals, the second alternative seems to be the most suitable site. This indicates that the results of the fuzzy goal programming model are valid. Despite the acceptable responses from the developed model, the result depends on the accuracy of the data collected from the field.
Conclusions
Selection of the most suitable site for a processing plant is a key step in the construction process, in that the results of this decision could have an important and long-term impact on various aspects on the plant and the related upstream and downstream industries. Owing to the cost of transportation of stone from quarries to the plant and the point of marketing, such plants are built near quarries and as close as possible to where the stone is marketed. Selection of the most desirable place to construct a processing plant to serve several quarries that are adjacent to each other is a consideration that has not yet been studied in other research, especially by multi-objective modelling. Accordingly, a multi-objective approach has been developed with fuzzy weights and priorities and using binary integer decision variables for a locality with four quarries, and three possible alternatives for a plant site. Local surveys and research were conducted, and information obtained from several experts was examined to determine acceptable numbers to start the activity. After introducing the fuzzy goal programming mathematical model, Excel® Solver was used to solve the model and determine the best site for plant construction. The best alternative was selected based on the shortest distance to the quarries, the workforce, and the high-voltage power source.
References
Arikan, F. 2013. A fuzzy solution approach for multi objective supplier selection. Expert Systems with Applications, vol. 40. pp. 947-952. [ Links ]
Aczel, J. and Saaty, T.L. 1983. Procedures for synthesizing ratio judgements. Journal of Mathematical Psychology, vol. 27, no. 1. pp. 93-102. [ Links ]
Izadikhah, M. 2015. A fuzzy goal programming based procedure for machine tool selection. Journal of Intelligent & Fuzzy Systems, vol. 28, no. 1. pp. 361-372. [ Links ]
Jadidi, O., Cavalieri, S., and Zolfaghari, S. 2015. An improved multi-choice goal programming approach for supplier selection problems. Applied Mathematical Modelling, vol. 39, no. 14. pp. 4213-4222. [ Links ]
Jinturkar, A.M. and Deshmukh, S.S. 2011. A fuzzy mixed integer goal programming approach for cooking and heating energy planning in rural India. Expert Systems with Applications, vol. 38, no. 9. pp. 11377-11381. [ Links ]
Jones, D.F. and Wall, G. 2015. An extended goal programming model for site selection in the offshore wind farm sector. Annals of Operations Research. DOI 10.1007/s10479-015-1828-2. [ Links ]
Kumar, M., Vrat, P., and Shankar, R. 2004. A fuzzy goal programming approach for vendor selection problem in a supply chain. Computers and Industrial Engineering, vol. 46, no. 1. pp. 69-85. [ Links ]
Lee, A.H.I., Kang, H.Y., and Chang, C.T. 2009 Fuzzy multiple goal programming applied to TFT-LCD supplier selection by downstream manufacturers. Expert Systems with Applications, vol. 38. pp. 6318-6325. [ Links ]
Safari, M., Ataei, M., Khalokakaei, R., and Karamozian, M. 2010. Mineral processing plant location using the analytic hierarchy process-a case study: the Sangan iron ore mine (phase 1). Mining Science and Technology, vol. 20, no. 5. pp. 691-695. [ Links ]
Safari, M., Khalokakaei, R., Ataei, M., and Karamozian, M. 2012. Using fuzzy TOPSIS method for mineral processing plant site selection. Arabian Journal of Geosciences, vol. 5. pp. 1011-1019. [ Links ]
Paper received Dec. 2015
Revised paper received Mar. 2017














