Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950
Print version ISSN 0378-4738
Water SA vol.41 n.1 Pretoria Jan. 2015
http://dx.doi.org/10.4314/wsa.v41i1.19
Surface-complexation modelling for describing adsorption of phosphate on hydrous ferric oxide surface
Haile A MengistuI, *; Abera TessemaII; Molla B DemlieIII, IV; Tamiru A AbiyeV; Oddvar RoeysetVI
IWayne County Comm unity College District, 801 W Fort St., Detroit MI 48226, USA
IIDepartment of Geology, University of Limpopo, Turfloop Campus, Sovenga 0727, Private Bag X1106, South Africa
IIISchool of Geological Sciences, University of Kwazulu-Natal, Private Bag X54001, Durban, South Africa
IVGNS Science, Private Bag 2000, Taupo, New Zealand
VSchool of Geosciences, University of the Witwatersrand, Private Bag X3, PO Wits 2050, Johannesburg, South Africa
VINorwegian Institute for Water Research (NIVA), Gaustadalleen 21, N-0349 OSLO, Norway
ABSTRACT
Adsorption of dissolved phosphate onto synthetic hydrous ferric oxide (HFO) was measured in the laboratory as a function of pH, ionic strength, and phosphate relative concentration. Experimental data were used to constrain optimal values of surface complexation reactions using a geochemical modeling code JCHESS according to the diffuse layer model. The results provide a consistent set of model equilibrium constant (log K) values at 25° C and 100 KPa for the following reactions:
>FeOH + PO43- + 3H+ = >FeO-H2PO4 + H2O (log K1int = 19.0)
>FeOH + PO43- + 2H+ = >FeO-HPO4- + H2O (log K2int = 14.3 ± 0.17)
>FeOH + PO43- + H+ = >FeO-PO42- + H2O (log K3int = 8.32 ± 0.27)
These results differ significantly from previously-published estimates of log K2int and log K3int [1-3], and provide a more accurate fit to experimental measurements over a broad range of pH (3-12), ionic strength (0.001-0.1 mol/ℓ) and total relative phosphate concentration (12-500 μmol phosphate/g HFO). The results provide a close fit to the experimental data within a wide range of conditions, and should be adopted in modelling the chemical speciation of phosphate in natural systems containing HFO as a predominant adsorbing material.
Keywords: phosphate, adsorption, hydrous ferric oxide, surface complexes, equilibrium constants
INTRODUCTION
Soluble phosphate salts are widely used as agricultural fertilisers to boost food production, and a common environmental problem associated with fertiliser overuse is elution of dissolved phosphate into ground and surface waters (Delgado and Torrent, 1997; Cisse and Mrabet, 2004). Elevated concentrations of soluble phosphate from agricultural discharges lead to eutrophication, anoxia, and degradation of freshwater habitats (Bennett et al., 2001). Natural background phosphate concentrations in freshwater settings typically vary between 0.095 and 0.95 mg/ℓ (Luisells et al., 2000), whereas in groundwater of heavily fertilised agricultural soils, it can generally reach levels of up to 2 mg/ℓ (Fadiran et al., 2007).
Under conditions where excess phosphate is not taken up through biological assimilation, temporary storage of labile phosphate in soils and aquifers occurs through adsorption onto mineral surfaces (Bowden et al., 1980; Dzombak and Morel, 1990; Nilsson et al., 1996; Geelhoed et al., 1997; Luisells et al., 2000; Dideriksen and Stripp, 2003) and refractory organic matter in sediments (Hiradate and Uchidan, 2004; Hutchison and Hesterberg, 2004). As a result, phosphate adsorption onto solid particles can provide a buffer against eutrophication of downstream systems, by slowing the throughput of phosphate in the vadose zone thereby decreasing the availability of dissolved phosphate to plant roots. Phosphate adsorption onto soil components can also influence the mobility of synthetic pesticides (Gimsing et al., 2004a; Gimsing et al., 2004b) impacting both water quality and ecosystem health.
Competitive adsorption of phosphate onto geologic media can enhance the mobility of other metal oxy-ligands such as arsenate and selenate (Manning and Goldberg, 1996; Geelhoed et al., 1997; Jackson and Miller, 2000; Bose and Sharma, 2002; Gao and Mucci, 2001) and the mechanism may be partially responsible for widespread arsenic contamination of groundwaters in heavily agricultural areas of Bangladesh and West Bengal (India), although other factors are reported to be causes of arsenic release (Bose and Sharma, 2002; Smedley and Kinniburgh, 2002). Jain and Loeppert (2000) investigated competitive phosphate and arsenate adsorption onto ferrihydrite, and found that phosphate uptake by ferrihydrite surfaces can substantially diminish arsenate sorption, thereby making dissolved arsenate available in solution, and that this effect is highly dependent on both pH and relative ligand activity. A study by Quaghebeur and Rengel (2004) found that addition of phosphate to soil media can increase free arsenate available for biological uptake, which was previously adsorbed onto soil particles. Phosphate coordination onto mineral surfaces can also influence cation speciation. For example, adsorption of phosphate onto goethite-coated quartz sand can enhance U(VI) adsorption due to the formation of >FeO-PO4-UO2, a ternary surface complex (Cheng et al., 2004). It is imperative that the principal reactions governing phosphate surface complexation in geologic systems is thoroughly understood because phosphate plays an important role in a wide variety of biogeochemical processes (Sherman and Randal, 2003; Karamalidis and Dzombak, 2010).
Experimentally-derived values for phosphate adsorption onto hydrous ferric oxide (HFO) reported in Dzombak and Morel (1990), Ryden et al. (1977a) and Ryden et al. (1977b) are perhaps the most commonly-referenced values used in surface complexation modelling studies. However, it is unclear to what extent these values can be applied rigorously across a range of geochemical conditions. Accurate model-dependent values for phosphate adsorption are necessary to quantify not only the speciation of phosphate itself, but also to describe and predict the speciation of phosphate in mixed systems containing other adsorbing solutes (Lee and Windt, 2001).
In the present study, the extent of phosphate adsorption onto HFO is measured in a controlled environment over a wide range of pH, background electrolyte (NaNO3) ionic strength, and relative phosphate concentration. HFO is chosen as a sorbent in the ongoing study because the surface property of HFO is very well characterised by several previous adsorption experiments (Hiemstra and Van Riemsdijk, 2009; Antelo et al., 2010; Liu et al., 2014; Villalobos and Antelo, 2011; Hofmann et al., 2004). The adsorption curves from the experiment are then used to constrain mass action parameters for phosphate surface complexation reactions with a geochemical code JCHESS on the basis of the diffuse layer model (DLM) (Dzombak and Morel, 1990). It has been found that FeO-PO4 forms a mono-dentate, bi-nuclear complex using X-ray absorption near edge structure (XANES) fingerprinting, and DLM is therefore appropriate to explain the adsorption process (Khare et al., 2007).
The outcome of the investigation is very important for understanding eutrophication of several reservoirs and lakes, and to broaden the current knowledge of various non-point phosphate pollution, mainly from agriculture. It also helps to understand the influence of phosphate speciation on the fate of other contaminants such as arsenate and selenate. Furthermore, the laboratory-based results can be applied to pilot-scale tests around phosphate plants and mines, where both phosphate and other trace metals are released into the environment in the presence of substantial solid particles.
MATERIALS AND METHODS
All source reagents used in the experiments were commercial (Fisher Scientific) reagent-grade materials, which were used without further purification unless otherwise specified. Solutions used in preparation of HFO and for adsorption experiments were prepared using 18 Mfl deionised water produced from a Barnstead Nanopure system. All glass- and plasticware used in the experiments were acid washed in trace metal grade HNO3 prior to use.
Preparation of HFO
Hydrous ferric oxide used in the experiments was prepared according to a previously-published procedure of Schwertmann and Cornel (2000). Forty (40) grams of Fe(NO3)3°9H2O or FeCl3 was dissolved in 500 mℓ of 18 MΩ water, and pH was adjusted to neutral value using approximately 300 m ℓ of 1 mol/ℓ KOH. KOH solution was gradually added to ferric nitrate/ferric chloride solution to achieve a pH of 7 to 8 after approximately 1 h of equilibration without any atmospheric CO2 exclusion. The resulting suspension was washed 6 times in 18 MΩ water, followed each time by centrifugation at 1 500 r/min for 5 min until no electrolyte is detected and conductivity of the supernatant is <10 μS/cm. The dialysed precipitate was freeze-dried in a LabConco™ sediment freeze drier to prevent the precipitates from mineralising to stable forms of ferric hydroxides such as goethite. The final precipitate was allowed to thaw afterwards at room temperature in a closed translucent Nalgene vessel for no more than 1 month prior to use. Some batches of HFO were manually ground with alumina mortar after being freeze-dried, while other batches were used in experiments without further modification.
HFO surface area and X-ray diffraction (XRD) measurement
Detailed surface characterisation of the sorbent (HFO) was conducted because surface complexation theory deals with interactions between the sorbate and the surface of the sorb-ent (in this case, HFO) (Dzombak and Morel, 1990; Khare et al., 2007; Karamalidis and Dzombak, 2010). Specific surface area for ground and un-ground HFO was measured using N2-adsorption Brunauer-Emmett-Teller (BET) analysis as an independent test of the qualitative effect of grinding and to assess the effect of the different HFO synthesis.
Two replica HFO samples having an estimated total surface area of 10 to 20 m2 (0.1 to 0.2 g) were put into thin glass tubes. The samples were first out-gassed in a vacuum for 2 and 24 h at temperatures of 50°C and 65°C. N2 gas, used as the analysis gas for surface area measurement, flowed into the sample tubes at different pressures to produce an adsorption isotherm. Specific surface area of the samples was calculated with the NovaChrome software, based on 11 point BET using sample density (assumed to be 3.8 g/ℓ) and the measured sample mass of each sample. The BET specific surface area measurement of a batch of HFO using FeCl3 and vacuum filtering was 96 m2/g, whereas surface area value of the HFO batch using Fe(NO3)3 and multiple centrifugation was 160 m2/g (Table 1). When the HFO samples of both batches were ground to roughly 4 nm , the specific surface area was 200-280 m2/g (Table 1). Repeated effort to synthesise HFO with surface area close to 650-750 m2/g reported in Dzombak and Morel (1990) did not succeed using the two-point method; similar HFO synthesis by Antelo and colleagues (Antelo et al., 2010) resulted in a surface area of 220 m2/g, significantly different from the ideal surface area of 650-750 m2/g. Possible causes of diminished surface area include uncertainty of the BET method (use of N2 gas with incomplete access to all available surface area), and a strong dehydration procedure as well as method uncertainties with the 2-point HFO synthesis procedure (Antelo et al., 2010).

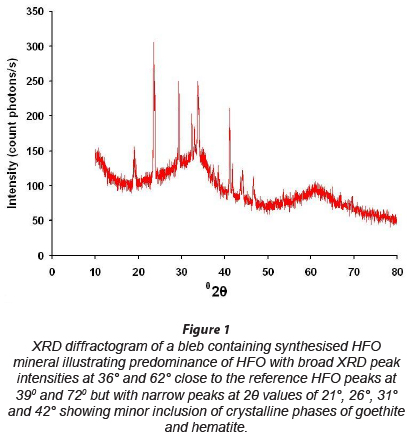
Powder XRD measurements were performed to characterise HFO synthesised in this study. The HFO, synthesised according to the procedure of Schwertmann and Cornell (2000), should result in 2-line ferrihydrite with broad XRD diffractogram peak intensities centered around 2Ө values of 39° and 72°. The measured XRD diffractogram has 2 broad peaks at 2Ө values of about 36° and 62°, which are comparable with the ideal 2-line diffractogram (Fig. 1). However, comparison with the typical diffractogram of hematite and goethite shows that sharp narrow picks in the measured diffractogram around 29 values of 20°, 26°, 31° and 42° may be due to the presence of very small amounts of mixtures of other phases of iron oxides of crystalline nature (hematite and goethite), possibly formed due to aging, freezing and thawing temperatures, and, to some extent, CO2 inclusion during HFO synthesis (Schwertmann and Cornell, 2000; Hofmann et al., 2004; Villalobos and Antelo, 2011).
Dissolved phosphate for adsorption experiments was prepared using a 1 000 μg/g P atomic absorption (AA) phosphorus standard (VWR brand) in 2% HNO3. Dissolved phosphate was diluted to an appropriate working concentration for each experiment using 18 Mfl water in various background electrolyte (NaNO3) concentrations (0.001-0.1 mol/ℓ). Electrolyte solutions were prepared using solid NaNO3 salt; to assess the influence of background electrolyte on phosphate adsorption.
Approximately 0.1 g of dry HFO was added to each of a series of parallel 50 mℓ polyethylene centrifuge tubes, into each of which was added 50 mℓ of NaNO3 solution containing varying initial concentrations of dissolved phosphate, to produce an overall HFO concentration of 2 g/ℓ and 24 to 1 000 μmol/ℓ phosphate. In each trial series, the pH of each separate 50 ml vessel was initially titrated manually to a desired pH range (~3 to 13) using 1 mol/ℓ NaOH and/or 0.1 mol/ℓ HNO3. Solution pH was measured potentiometrically using an epoxy semi-micro pH combination electrode and handheld meter (VWR brand). Vessels were placed on a rotating mixer and allowed to equilibrate for 2 h, after which pH was re-adjusted as necessary. Vessels were then allowed to equilibrate for an additional 22 h. After 24 h total equilibration time, the pH of each vessel was measured and centrifuged at 5 000 g for 15 min to separate colloidal HFO from supernatants. Three (3) mℓ of supernatant was removed from the upper portion of each centrifuged vessel, and analysed for dissolved phosphorus using the colorimetric ascorbic E procedure of Eaton and Franson (2005; Standard Methods). Colorimetric measurements were made using a Spectrocam UV/Vis spectrophotometer.
Following the procedures developed to evaluate the influence of carbonate co-adsorption in the adsorption of various chemical species in the presence of goethite nano-particles, CO2 exclusion adsorption experiments were conducted based on various solution pH conditions (Villalobos and Leckie, 2001; Kanematsu et al., 2011). The adsorption under both closed (fixed total CO2) and open (fixed PCO2) conditions was conducted to assess the potential influence of dissolved bicarbonate and carbonate on phosphate adsorption onto HFO. The closed experiment involves careful exclusion of CO2(g) from the phosphate adsorption experiment with a Coy glove-box anaerobic chamber containing an atmosphere of 95% N2 and 5% H2. Carbon dioxide exclusion experiments were performed using similar methodology as those completed in air. For all experiments parallel controls were maintained that contained dissolved phosphate, but no HFO.
The kinetics and reversibility of phosphate adsorption onto HFO were measured in a separate set of experiments. In these trials, dissolved phosphate (500 and 1 000 μmol/ℓ) was combined with 2 g/l of HFO in 1 l volume Nalgene reaction vessels in 0.01 mol/ℓ NaNO3 at a pH of 2.65 (Fig. 2). Reaction vessels were allowed to equilibrate in air under constant vigorous stirring on a magnetic stir plate. Aliquots were removed by syringe as a function of time from reaction vessels and filtered to 0.2 μm through fresh Nylon syringe filters. Filtered aliquots were analysed for dissolved phosphate by colorimetric spectro-photometry. Phosphate was allowed to adsorb onto HFO for up to ~12 h, after which pH of solutions was adjusted to 12 and the systems were allowed to re-equilibrate. Over the next 40 h, sample aliquots were extracted, filtered, and analysed for eluted phosphate by colorimetric spectrophotometry.
Surface complexation modelling
Results of phosphate adsorption experiments were modelled using the chemical speciation program JCHESS (*) and its associated thermodynamic database (Lee and Wendt, 2001). JCHESS speciation software was used to calculate the extent of phosphate surface complexation onto HFO as a function of phosphate/HFO relative concentration, pH and NaNO3 ionic strength using literature values for phosphate adsorption onto HFO provided in Dzombak and Morel (1990), Ryden et al. (1977a) and Ryden et al. (1977b) for a DLM depiction.
Speciation calculations took account of aqueous compl-exation reactions involving all dissolved electrolyte and pH titrant ions (Na+, NO3-), autoionisation of water, and the specia-tion effects of atmospheric CO2 dissolution (for experiments conducted in air) and aqueous complexation (Sverjensky and Sahai, 1996). Activity coefficients for aqueous species were calculated using a Debye-Huckel model. JCHESS modelling of experimental data was carried out by calculating the predicted fraction of dissolved and adsorbed phosphate as a function of pH for each experimental trial series at constant initial phosphate, HFO and ionic strength in NaNO3. The calculated pH-dependent distribution of phosphate was compared with the appropriate set of experimental results.
The values for mass action parameters (equilibrium constants) for specific phosphate adsorption relations were itera-tively adjusted to achieve an optimal overall fit to the trend of experimental data for each series. Phosphate adsorption onto HFO was hypothesised to occur by the formation of 3 different monodentate surface complexes (Dzombak and Morel, 1990; Ryden et al., 1977a; Ryden et al., 1977b):
where:
>FeOH represents a proton-exchanging surface hydroxyl site on HFO (Dzombak and Morel, 1990).
For each of Eqs (1) to (3) the mass action expression governing surface complexation of the appropriate phosphate aqueous species can be described according to the conventional equilibrium expression, taking account of electrostatic effects that cause deviation between the apparent (Kapp) and intrinsic (Kint) equilibrium constants (Eq. (4)):

where:
the exponential term defines a coulombic correction to Kapp that may be calculated from the change in surface charge accompanying the reaction (AZ), Faraday's constant (F), the electrical potential at the HFO surface (y), the universal gas constant (R) and temperature (T).
The electrical potential at the HFO surface is determined according to the mass law and mass action expressions for intrinsic hydrolysis at the HFO-water interface, and DLM constraints relating surface charge to potential (Dzombak and Morel, 1990; Stumm and Morgan, 1996; Saha and Streat, 2005).
RESULTS
Experimental results
Results of phosphate adsorption experiments onto HFO are shown in Figs 4-9, for uptake of 12-500 μmol phosphate/g HFO as a function of pH, in 0.001 to 0.1 mol/ℓ NaNO3 background electrolyte. In general the results of phosphate adsorption experiments conform to expectations based on previous studies of ligand adsorption (Dzombak and Morel, 1990; Ryden et al., 1977a; Ryden et al., 1977b) that uptake of phosphate by HFO is minimal at pH values greater than about 12, increases at lower pH values across a characteristic adsorption edge, and that maximum uptake is achieved at pH values below 8.
In the current study, phosphate adsorption onto HFO shows little ionic strength dependence at low to circum-neutral pH, but at high pH values adsorption is substantially more dependent on ionic strength (Fig. 2). At high pH values, phosphate adsorption is diminished relative to circum-neutral conditions, and is further diminished as ionic strength decreases, from approximately 50% adsorption at 0.1 mol/ℓ NaNO3, to insignificant adsorption at 0.001 mol/ℓ NaNO3 (Fig. 2). These results are consistent with inner-sphere binding of phosphate onto the HFO surface, as has been shown previously (Persson et al., 1996; Torrent et al., 1990; Saha and Streat, 2005).
Reversibility experiments were performed at 250 and 500 μmol phosphate/g HFO, and the results of these studies are shown in Fig. 3. Sorption of available phosphate at a pH of 3 was initially rapid, and reached an apparent maximum after approximately 3 h. Desorption at a pH of 11.3 was slower, and elution of only about 70% of adsorbed phosphate was observed after 800 min. The results of adsorption experiments reveal that even at a pH of approximately 25-30% of available phosphate is taken up by HFO, but combining this fraction with the observed extent of reversed desorption nonetheless indicates that at a pH of 11.3 about 25% of adsorbed phosphate is retained irreversibly by the HFO within the duration of the experiments. These results are consistent with previous studies, which have shown that phosphate sorption by ferric oxides is partially irreversible over short timescales, mostly because of slow kinetics of inner-sphere complex detachment (Torrent et al., 1990; Torrent and Delgado, 2001).
Comparison of the CO2 free adsorption experiment with those completed in the presence of air demonstrates that the effect of CO2 is negligible in causing any change in the equilibrium constant of high pH adsorption (Fig. 4). Similarly, a previous investigation reported weak carbonate adsorption on goethite surface (Kanematsu et al., 2011). The measured adsorption edge generally diminished slightly, especially at high pH ranges (pH > 8) in the open system (CO2-inclusion) compared to adsorption edges conducted in closed setup (CO2-excluded) (Fig. 4). The data is not unexpected but it is also evident that the reduction is not significant enough to modify the calculated adsorption equilibrium constants.
At 500 μmol phosphate/g HFO approximately 80% of available phosphate is taken up by HFO at pHs ranging between 6 and 7 (Figs 5a and 5b). All available dissolved phosphate is taken up by HFO at low pH, and up to 250 |mol phosphate/g HFO. At a phosphate loading of greater than 250 μmol phosphate/g HFO, adsorption curves as a function of pH display a distinct inflection, presumably suggesting discrete adsorption of a least two separate surface species (Figs 5a and 5b). At high pH values, phosphate adsorption was negligible at phosphate loadings less than 125 μmol phosphate/g HFO, but at greater phosphate loadings significant uptake (20-25% of available phosphate) was observed up to the maximum experimental pH of ~12 (Figs 6 and 7). At low phosphate loading (12-62.5 μmol phosphate/g HFO) adsorption edges are sharp, but become less steep with increasing relative phosphate concentration (Figs 8 and 9).
At the estimated specific surface area of 120 m2/g, obtained from modelling calculations, a maximum phosphate adsorption capacity of roughly 3.3 μmol phosphate/m2 HFO is equated, corresponding closely with the range of published values for the phosphate adsorption capacity of ferrihydrite (2.4-3.9 μmol P/m2) (Torrent et al., 1990). Moreover, it is consistent with the recommended site density of the low-energy (weak) site on HFO, 3.11 μmol/m2, provided by Dzombak and Morel (1990); Ryden et al. (1977a) and Ryden et al. (1977b), which was used in this study.
Results of surface complexation modeling
JCHESS model calculations were used to fit the experimental data using a depiction of phosphate binding at the HFO surface governed by 3 different monodentate surface species, as illustrated in Eqs (1), (2) and (3). Previous spectroscopic work (Persson et al., 1996) shows that orthophosphate adsorption onto goethite is likely dominated by monodentate surface complexes involving >FeO-H2PO4, >FeO-HPO4-, and >FeO-PO42-, whereby each species binds separately onto a low-energy proton-exchangeable surface site, with little contribution from bidentate or bridging complexes (Hoell and Kalinichev, 2004). A similar depiction was adopted by Dzombak and Morel (1990), Ryden et al. (1977a) and Ryden et al. (1977b,) for phosphate adsorption onto HFO. The model was used to evaluate phosphate adsorption onto HFO in the current study, according to a DLM surface complexation scenario.
Table 2 provides optimal estimates of intrinsic equilibrium constants for reactions (1), (2) and (3) governing phosphate adsorption onto HFO, constrained by the experimental data obtained in this study. Separate optimisations were performed for each set of experimental data at a particular set of ionic strength and phosphate-loading conditions. Optimisations for each set of experimental data provided model-dependent estimates for the values of all three adsorption equilibrium constants. Mean values for the three pertinent equilibrium constants, obtained by averaging model results from 12 separate sets of experimental data spanning 12-500 μmol phosphate/g HFO and 0.1 to 0.001 mol/ℓ electrolytes, are provided in Table 2. The model values are highly reproducible, as shown by relatively low percentage standard deviation values (1.2% to 3.3%), representing a one-sigma sample standard deviation range of 0.17 to 0.27 log units for the three estimated equilibrium constants. The optimal values for logarithms of equilibrium constants of >FeO-HPO4- and >FeO-PO42- complexes are 14.2 ± 0.17, and 8.3 ± 0.27, respectively. The same value for >FeO-H2PO4 adsorption, 19.0, was used in all calculations. It was found that model calculations at less than 250 |mol phosphate/g HFO were insensitive to the chosen value of log K1intbecause there is complete adsorption at lower loadings and lower pH conditions, but model insensitivity does not diminish the significace of the >FeO-H2PO4 surface complex.
The optimal value for log K2int (14.2) describing HPO42-adsorption generated in the current experiment differs from the value of 13.04 recommended by Ryden et al. (1977a) and Ryden et al. (1977b), and predicts a slightly more stable >FeO-HPO4-surface complex. The optimal value for stability of the surface >FeO-PO42- species (log K3int = 8.3) is 3 orders of magnitude greater than the earlier estimate of 5.37 (Ryden et al., 1977a; Ryden et al., 1977b), predicting a substantially greater tendency for PO43- adsorption.
DISCUSSION
The optimal model equilibrium constants provided in Table 2 were calculated using experimental data at 3 different estimated specific surface areas, ranging from 60 m2/g to 120 m2/g. A range of surface areas was used because of different HFO preparation methods used in this study; subsequent to freeze-drying, some batches of HFO were ground in an alumina mortar prior to use, which resulted in a smaller average grain size of roughly 4 nm to achieve a qualitatively representative specific surface area. This approach allowed constraining of phosphate adsorption edges with surface complexation modelling using DLM under a range of various HFO specific surface area. The majority of the experiments were conducted in mixture of the HFO samples with surface areas ranging from 96-220 m2/g. Various values for laboratory synthesised surface areas of HFO have been reported, including 200-750 m2/g by Hofmann et al. (2004) and 200-350 m2/g by Hiemstra et al. (2009). On the other hand, Villalobos and Antelo (2011) compiled HFO surface areas ranging from 300 up to 1 120 m2/g, indicating the wide range of measured specific surface area. According to Villalobos and Antelo (2011), aging, freezing temperature and carbonate inclusion can cause various HFO-specific surface areas. Technical difficulty in completely excluding atmospheric CO2 during HFO synthesis and subsequent particle growth was suggested as the main cause of diminished specific surface area (Villalobos and Antelo, 2011). HFO synthesis at high Fe concentration was also suggested as a possible cause of reduced surface area by Hiemstra et al. (2009). Antelo et al. (2010) recommended conducting potentiometric titration at various background electrolyte ionic strengths to estimate a compromise surface area, provided that the freshly synthesised HFO does not aggregate into a more crystalline form. Hofmann et al. (2004) concluded that exclusion of CO2 was achieved through N2 gas bubbling during HFO synthesis, but the theoretical surface area was not achieved. The relatively lower specific surface areas in this study are highly likely to have been caused by aging and carbonate inclusion during HFO synthesis.
Measured surface area values were not adopted quantitatively in surface complexation modelling exercises because, when used alongside the recommended HFO weak-site density of 3.11 μmol/m2 (Dzombak and Morel, 1990; Ryden et al., 1977a; Ryden et al., 1977b), anomalously low values (by several orders of magnitude) are predicted for phosphate adsorption equilibrium constants of surface complexes of >FeO-H2PO4, >FeO-HPO4-, and >FeO-PO42-. A possible explanation could be the adsorption isotherm data covering a narrow range of pH values.
Reactive site density is difficult to estimate experimentally from various saturation of surface sites with ions (Hiemstra et al., 2009). Villabos and Antelo (2011) reported a range of values of reactive site density for HFO between 8.8 and 9.1 nm-2, whereas Hiemstra et al. (2009) distinguished site densities with respect to coordination of surface groups as singly cordinated groups forming bidentate complexes and double corner/edge sharing with 2.5 ± 0.1 and 3.5 ± 0.4 nm-2, respectively, as well as 1.2 ± 0.2 nm-2 for triply coordinate surface groups. The data presented in this research, albeit with a different unit, is comparable to the value suggested by Dzombak and Morel (1990) and Svjerjensky (2003). Therefore a compromise was adopted in this study, where a site density of 3.11 |mol/m2 was assumed, and a surface area of 120 m2/g was constrained by an optimal fit to the trends in experimental data obtained in 500 μmol phosphate/g HFO experiments (maximum loading), as shown in Fig. 5. Table 2 shows that, although the specific surface area constrained by the model in this study is lower than most values, the final surface complexation constant would not be significantly altered.
In an effort to minimise errors associated with variable surface areas, and to standardise model equilibrium constants of the study to values that may be applied to a wide range of potential conditions, the predicted values of the current investigation were recalculated to be consistent with the proposed standard state of Sverjensky (2003) for mineral surface sites and species. Sverjensky (2003) reported that equilibrium constants for conventional surface complexation reactions such as Eqs (1), (2) or (3) may be recalculated in reference to an arbitrary standard state according to the following equation:

where:
Kint is the apparent intrinsic equilibrium constant under arbitrary conditions at 298 K and 100 KPa NSis surface site density of the solid sorbent (sites/m2)
AS is the specific surface area of the solid sorbent (m2/g)
CS is the amount of sorbent present (g/ℓ)
N# is the hypothetical site density at the adopted standard state
A# is the hypothetical specific surface at the adopted standard state
KΘ int is the standard state intrinsic equilibrium constant
A hypothetical surface site density of 1018 sites/m2 and a hypothetical specific surface area of 10 m2/g at standard reference condition was adapted from Sverjensky (2003). The model values for log K1int, log K2int and log K3int, recalculated in terms of log KΘ1int, log KΘ2int and log KΘ3int, are shown in Table 2. The relative standard deviations among individual model values for log KΘ2int and log KΘ3int are smaller in magnitude than those for log K2int and log K3int.
The results of the current investigation are compiled based on the work of Sverjensky (2003), which show that deviations among model values for adsorption equilibrium constants can be minimised by accounting for differences in assumed mineral properties via a reference-state correction such as Eq. (5). In the case of log K1int, one value was used for all model calculations, while different surface areas were used; therefore Eq. (5) produces a variance in log KΘ1int values that is an artefact of the calculation. The recalculated standard-state equilibrium constants shown in Table 2 may be compared directly with those obtained in other experiments where different values for specific surface area or site density have been assumed, by rearranging Eq. (5) appropriately and solving for the desired values. Equilibrium constants of different reactions, obtained by different authors, and calculations based on different assumptions regarding the HFO surface, may be reconciled quantitatively and used in concert to provide an improved depiction of chemical speciation equilibria under a wide range of conditions.
Figures 5-9 illustrate model curves for phosphate adsorption onto HFO using the estimated log K1int, log K2int and log K3int values (solid lines), calculated using JCHESS, alongside the experimental data. The figures also depict model curves (dotted lines) that are calculated using the recommended phosphate adsorption equilibrium constants of Ryden et al. (1977a) and Ryden et al. (1977b). The trends shown in Figs 5-9 demonstrate that the values of Ryden et al. (1977a) and Ryden et al. (1977b) cannot account for phosphate adsorption throughout the range of conditions examined in this study, and substantially underestimate the extent of phosphate adsorption at circum-neutral to basic pH conditions, and at low loading. The extent of underestimation is greatest under conditions where PO43- accounts for a substantial fraction of dissolved phosphate activity, because the principal difference between earlier estimates of phosphate adsorption and the estimates obtained in this study lie in the predicted stability constant of the >FeO-PO42- surface complex.
Under acidic pH conditions, there is little difference between the previous and newly predicted values of log K1int and log K2int, mainly because of maximum phosphate adsorption. Quantum mechanics calculation was used by Wang et al. (2013) to postulate that diprotonated bi- and mono-dentate complexes dominate phosphate adsorption on HFO within a pH range of 4 to 6 . Similar conclusions were drawn by Antelo et al. (2010), whereas Luengo et al. (2006) proposed protonated bidentate phosphate surface complexes at lower pH condition using attenuated total reflection-infrared (ATR-IR) spec-troscopic measurements. On the other hand the presence of non-protonted bidentate complexes at pH 7.5 was confirmed by Arai and Sparks (2002). Nevertheless, the majority of previous studies did not rule out the presence of unidentified surface species at various pHs. It was also suggested that conclusions drawn regarding surface complexes of HFO are generally taken based on goethite as a proxy mineral and therefore HFO surface characterisation still lacks accuracy (Antelo et al., 2010; Kare et al., 2011; Arai and Sparks, 2002).
The phosphate loading, being much lower than the available reactive site density, must also be taken into consideration to avoid precipitaiton. In this instance, precipitation is ruled out because it has been confirmed that the adsorption reaction within or lower than the maximum site density is reversible with the kinetic experiments (Fig. 2). At higher pH values, especially above the pH of zero proton charge (PZPC of ~8.7), the HFO surface (>FeOH-) is deprotonated having a net negative charge, which tends to electrostatically repulse the dominating aqueous phosphate species HPO42- and PO43- (Antelo et al. 2010). The discrepancy observed between this study and the previously published surface complexation constant (K2) for circum-neutral to pH 8.7 is marginal, implying that the surface complexes and the actual model predictions are fairly acceptable.
However, at sufficiently higher pH, the significant difference (up to 3 orders of magnitude) between the calculated and published K3 value can only be justified by the presence of unidentified surface species, as suggested by previous publications (Antelo et al. 2009; Luengo et al. 2006; Arai and Sparks, 2002). It is anticipated that significant errors could arise when values of Ryden et al. (1977a) and Ryden et al. (1977b) are used to predict the reactive transport of phosphate, for instance, in carbonate-buffered aquifers, as those values substantially under-predict the extent of phosphate adsorption under neutral to basic conditions. The modest discrepancy between the model and the measured analytical data in this study could most likely be explained by the interference of carbonates, especially at higher phosphate loading and sufficiently higher pH values consistent with the carbonate co-adsorption on goethite results of Villalobos and Leckie (2001) and Kanematsu et al. (2011).
The combined adsorption edges of the various phospate loadings (12 μmol/ℓ p/g HFO - 500 μmol/ℓ p/g HFO) demonstrate sharp adsorption edges in low phosphate loadings when compared to adsorption edges at higher phosphate loadings (Fig. 10). The model-fitting exercise, with a close match between predicted and measured adsorption edges, is qualitative evidence that singly-coordinated surface groups dominate the entire pH range, in line with previously published studies (Antelo et al. 2010; Hiemstra et al. 2009).
In the pH range higher than 8.7, >FeO-HPO4- and >FeO-PO42- are the dominant surface complexes. In this investigation, the inclusion of triply-coordinated surface groups in the model exercise did not improve the fits and therefore was not considered to contribute significantly to the adsorption process. Direct surface spectroscopic measurements by various researchers indicate that there are unidentified surface groups (Antelo et al. 2009; Luengo et al. 2006; Arai and Sparks, 2002) suggesting that there is a high level of uncertainty in the existing knowledge of HFO surface complexes at higher pH values. Previously published works of Wang et al. (2013), Antelo et al. (2010), Kare et al. (2011) and Arai and Sparks (2002) show that the non-protonated mono-dentate binuclear complex is the predominant mode of phosphate adsorption on the three Fe (hydr)oxides. The improved model-fits achieved in the current investigation, within a wide range of pH conditions, various phosphate loadings and background electrolyte ionic strengths, qualitatively suggest insignificant contribution of other surface complexes not incorporated in the modelling process.
Moreover, under natural conditions where extreme phosphate loading is present, as in heavily over-fertilised agricultural settings, the current model results do not predict substantially different phosphate speciation than would the values of Ryden et al. (1977a) and Ryden et al. (1977b), unless pH is greater than ~8. However, at lower phosphate loading, typical of most polluted natural settings, the results from the current study demonstrate, and predict, substantially more phosphate adsorption onto HFO under circum-neutral to basic pH conditions.
CONCLUSIONS
Adsorption of dissolved phosphate onto synthetic hydrous ferric oxide (HFO) was measured in the laboratory as a function of pH, ionic strength, and phosphate relative concentration. An increase in background ionic strength showing enhanced adsorption, especially at high loadings and high pH conditions, implies that phosphate adsorption on HFO is an inner-sphere ligand exchange process. A reversibility expriment confirms that phosphate adsorption within the measured phosphate loadings and solution conditions is a ligand exchange reaction with no or negligible precipitation.
Relatively low specific area surface of HFO nano-particles measured in the current study is likely due to agregation caused by ageing and freezing-thawing temperatures as well as difficulty in excluding CO2 during the HFO sythesis process. Three complexation constants with singly coordinated >FeO-H2PO4, >FeO-HPO4- and >FeO-PO42- surface complexes fairly describe the adsorption process within a wide range of solution conditions. The fit for the complexation constant (K3) at higher pH conditions (pH > 9.5) is more accurate than previously published values and may be compared directly and quantitatively with adsorption equilibria for other reactions obtained by assuming different properties for the HFO surface. The minor discepancy between the modelled and measured adsorption data in this study can be best explained by unidentified surface complexes, as confirmed by direct spectroscopic surface characterisations.
ACKNOWLEDGEMENTS
The authors would like acknowledge Prof. Carla Korestky for her critical advices and input to the manuscript. The authors would also like to thank Western Michigan University, Department of Geosciences, for laboratory facilities and research funding.
REFERENCES
ANTELO J, FIOL S, PERES C, MARINO S, ARCE F, GONDAR D and LOPEZ R (2010) Analysis of phosphate adsorption onto ferrihydrite using the CD-MUSIC model. J. Colloid Interface Sci. 347 112-119. [ Links ]
ARAI Y, SPARKS DL (2002) ATR-FTIR spectroscopic investigation on phosphate adsorption mechanisms at the ferrihydrite-water interface. J. Colloid Interface Sci. 371 (2) 317-326. [ Links ]
BENNETT E, CARPENTER S and CARAVAN N (2001) Human impact on erodable phosphorus and eutrophication: A global perspective. BioScience 51 227-234. [ Links ]
BOWDEN J, NAGARJAH S, BARROW J, POSNER A and QUIRK J (1980) Describing the adsorption of phosphate, citrate and selenate on a variable-charge mineral surfaces. Aust. J. Soil Sci. 18 49-60. [ Links ]
BOSE P and SHARMA A (2002) Role of iron in controlling speciation and mobilization of arsenic in subsurface environment. Water Res. 36 4916-4926. [ Links ]
CHENG T, BARNETT MO, RODEN EE and ZHUANG JL (2004) Effects of phosphate on uranium-VI adsorption to goethite-coated sand. Environ. Sci. Technol. 38 6059-6065. [ Links ]
CISSE L and MRABET T (2004) World phosphate production: Overview and prospects. Phosphorus Res. Bull. 15 21-25. [ Links ]
DELGADO A and TORRENT J (1997) Iron-related phosphorus in overfertilized European soils. Eur. J. Agron. 6 205-214. [ Links ]
DIDERIKSEN K and STRIPP L (2003) The adsorption of glyphosate and phosphate to goethite: a molecular-scale atomic force microscopy study. Geochim. Cosmochim. Acta 67 (18) 3313-3327. [ Links ]
DZOMBAK D and MOREL F (1990) Surface Complexation Modeling: Hydrous Ferric Oxide. Wiley Company, New York. 393 pp. [ Links ]
EATON AD and FRANSON MH (eds) (2005) Standard Methods for the Examination of Water and Waste Water. American Public Health Association, Washington DC. 1 368 pp. [ Links ]
FADIRAN AO, DLAMINI SC and MAVUSO A (2007) A comparative study of the phosphate levels in some surface and ground water bodies of Swaziland. Bull. Chem. Soc. Ethiop. 22 (2) 197-206. [ Links ]
GAO Y and MUCCI A (2001) Acid-base reactions of phosphate and arsenate complexation and their competitive adsorption adsorption at the surface of goethite in 0.7 m NaCl solution. Geochim. Cosmochim. Acta 165 (14) 2361-2378. [ Links ]
GEELHOED J, HIEMSTRA T and VAN RIEMSDIJK W (1997) Phosphate and sulfate adsorption on goethite: Single anion and competitive adsorption. Geochim. Cosmochim. Acta 61 (1 2) 2389-2396. [ Links ]
GIMSING AL, BORGGAARD OK and SESTOFT P (2004) Modeling the kinetics of the competitive adsorption and desorption of glyphosate and phosphate on goethite and gibbsite and in soils. Environ. Sci. Technol. 38 1718-1722. [ Links ]
GIMSING AL, BORGGAARD OK and BANG M (2004) Influence of soil composition on adsorption of glyphosate and phosphate by contrasting Danish surface soils. Eur. J. Soil Sci. 55 183-191. [ Links ]
HIRADATE S and UCHIDA N (2004) Effects of soil organic matter on pH-dependent phosphate sorption by soils. Soil Sci. Plant Nutr. 50 665-675. [ Links ]
HIEMSTRA T and VAN RIEMSDIJK WH (2009) A surface structural model for ferrihydrite I: sites related to primary charge, molar mass, and mass density. Geochim. Cosmochim. Acta 73 (1 5) 4423-4436. [ Links ]
HOELL W and KALINICHEV A (2004) The theory of formation of surface complexes and its application to the description of multi-component dynamic sorption systems. Russ. Chem. Rev. 73 351-370. [ Links ]
HOFMANN A, PELLETIER M, MICHOT L, STRADNER A, SCHURTENBERGER P, KRITZSCHMAR R (2004) Characterization of the pores of hydrous ferric oxide aggregates formed by freezing and thawing. J. Colloid Interface Sci. 271 163-173. [ Links ]
HUTCHISON KJ and HESTERBERG DJ (2004) Dissolution of phosphate in a phosphorus-enriched ultisol as affected by microbial reduction. J. Environ. Qual. 33 1793-1802. [ Links ]
JACKSON P and MILLER P (2000) Effectiveness of phosphate and hydroxide for desorption of arsenic and selenium species from iron oxides. Soil Sci. Soc. Am. J. 64 1616-1622. [ Links ]
JAIN A and LOEPPERT RH (2000) Effect of competing anions on the adsorption of arsenate and arsenite by ferrihydrite. J. Environ. Qual. 29 1422-1430. [ Links ]
KANEMATSU M, YOUNG T, FUKUSHI K, SVERJENSKY D, GREEN GP and DARBY LJ (2011) Quantification of the effects of organic and carbonate buffers on arsenate and phosphate adsorption on a goethite-based granular porous adsorbent. Environ. Sci. Technol. 45 (2) 561-568. [ Links ]
KARAMALIDIS A and DZOMBAK D (2010) Surface Complexation Modeling: Gibbsite. Wiley Company, New Jersey. 304 pp. [ Links ]
KHARE N, MARTIN DJ and HESTERBERG D (2007) Phosphate bonding configuration on ferrihydrite based on molecular orbital calculations and XANES fingerprinting. Geochim. Cosmochim. Acta 71 (14) 4405-4415. [ Links ]
LEE JVD and WINDT LD (2001) Present state and future directions of modeling of geochemistry in hydrogeological systems. J. Contam. Hydrol. 47 265-282. [ Links ]
LENOBLE V, BOURAS O, DELUCHAT V, SERPAUD B and BOLLINGER JC (2002) Arsenic adsorption onto pillared clays and iron oxides. J. Colloid Interface Sci. 255 52-58. [ Links ]
LIU H, LI X, WANG Y, YANG X, ZHEN Z, CHEN R, HOU D and WEI Y (2014) New insights into the effect of the formation environment of ferrihydrite on its structure and properties. RSC ADV. 411451-11458. [ Links ]
LUENGO C, BRIGANTE M and AVENA M (2006) Kinetics of phosphate adsorption on goethite: comparing batch adsorption and ATR-IR measurements. J. Colloid Interface Sci. 300 (2) 511 - 518. [ Links ]
LUISELLS C, ELSABETTA B and FRANCO M (2000) Sorption of phosphate on goethite at high concentrations. Soil Sci. 165 (3) 657-664. [ Links ]
MANNING B and GOLDBERG S (1996) Modeling competitive adsorption of arsenate with phosphate and molybdate on oxide minerals. Soil Sci. Soc. Am. J. 60 121-13. [ Links ]
NILSSON N, PERSSON P, LOVGREN L and SJOBERG S (1996) Competitive surface complexation of o-phtalate and phosphate on goethite particles. Geochim. Cosmochim. Acta 60 (22) 4385-4395. [ Links ]
PERSSON P, NILSSON N and SJOBERG S (1996) Structure and bonding of orthophosphate ions at the iron oxide-aqueous interface. J. Colloid Interface Sci. 177 263-275. [ Links ]
QUAGHEBEUR M and RENGEL Z (2004) Phosphate and arsenate interactions in the rhizosphere of canola (Brassica napus). Funct. Plant Biol. 31 1085-1094. [ Links ]
RYDEN JC, MCLAUGHLIN JR and SYERS JK (1977) Mechanisms of phosphate sorption by soils and hydrous ferric oxide gel. J. Soil Sci. 28 72-92. [ Links ]
RYDEN JC, MCLAUGHLIN JR and SYERS JK (1977) Time-dependent sorption of phosphate by soils and hydrous ferric oxides. J. Soil Sci. 28 585-595. [ Links ]
SAHA B and STREAT M (2005) Adsorption of trace heavy metals: Application of surface complexation theory to a macroporous polymer and a weakly acidic ion-exchange resin. Ind. Chem. Res. 44 (23) 8671-8681. [ Links ]
SCHWERTMANN U and CORNELL RM (2000) Iron Oxides in the Laboratory: Preparation and Characterization. Wiley-VCH Company, Weinheim. 188 pp. [ Links ]
SHERMAN D and RANDAL S (2003) Surface complexation of arsenic(V) to iron(III) (hydr)oxides: Structural mechanism from ab initio molecular geometries and EXAFS spectroscopy. Geochim. Cosmochim. Acta 67 (22) 4223-4230. [ Links ]
SMEDLEY PL and KINNIBURGH DG (2002) A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 17 (5) 517-568. [ Links ]
STUMM W and MORGAN JJ (1996) Aquatic Chemistry and Rates in Natural Waters. Wiley Company, New York. 1022 pp. [ Links ]
SVERJENSKY DA (2003) Standard states for the activities of mineral surface sites and species. Geochim. Cosmochim. Acta 67 17-28. [ Links ]
SVERJENSKY D and SAHAI N (1996) Theoretical prediction of single site surface protonation equilibrium constants for oxides and silicates in water. Geochim. Cosmochim. Acta 60 (20) 3773-3797. [ Links ]
TORRENT J and DELGADO A (2001) Using phosphorus concentration in the soil solution to predict phosphorus desorption to water. J. Environ. Qual. 30 1829-1835. [ Links ]
TORRENT J, SCHWERTMANN U and BARRON V (1990) Phosphate adsorption and desorption by goethites differing in crystal morphology. Soil Sci. Soc. Am. J. 54 1007-1012. [ Links ]
VILLALOBOS M and LECKIE J (2001) Surface complexation modeling and FTIR study of carbonate adsorption to goethite. J. Colloid Interface Sci. 235 (1) 15-32. [ Links ]
VILLABOS M and ANTELO J (2011) United surface structural model for ferrihydrite proton charge, electrolyte binding and arsenate adsorption. Rev. Int. Contam. Ambient 27(2) 139-151. [ Links ]
WANG X, LIU F, TAN W, LI W, FENG X and SPARKS DL (2013) Characteristics of phosphate adsorption-desorption onto ferrihy-drite: comparison with well-crystalline Fe (hydr)oxides. Soil Sci. 178 1-11. [ Links ]
Received 8 June 2013
Accepted in revised form 8 January 2014
* To whom all correspondence should be addressed. +17345020743; e-mail: hmengis1@wcccd.edu; hrmengistu@gmail.com















