Services on Demand
Journal
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Water SA
On-line version ISSN 1816-7950Print version ISSN 0378-4738
Water SA vol.41 n.1 Pretoria Jan. 2015
https://doi.org/10.4314/wsa.v41i1.9
Effects of data resolution and stream delineation threshold area on the results of a kinematic wave based GIUH model
Asghar AzizianI; Alireza ShokoohiII, *
IHydraulic Structure Department, Tehran University, PO Box 4111, Karaj, Iran
IIWater Engineering Department, Faculty of Engineering and Technology, Imam Khomeini International University, Qazvin 34149 - 16818, Iran
ABSTRACT
This research addresses the effect of using digital elevation models (DEMs) derived from different sources on the results of a kinematic wave based GIUH model. DEMs from different sources exhibit data-resolution effects on the important derived geomorphological properties of watersheds used in rainfall-runoff modelling. Using DEMs derived from topography maps (TOPO DEM) and the SRTM DEM, it was illustrated that different threshold areas for stream network extraction affect GIUH model performance. The results show that the SRTM DEM gives higher values for sub-basin and channel slope as well as number of streams, than the TOPO DEM, while mean length of overland and channel flow is greater for the latter source. The results also indicate that peak flow and slope of the hydrograph rising limb obtained from the SRTM DEM at different threshold areas (ranging from 0.25% to 3%) are greater than that for the TOPO DEM. Investigating the effects of stream network delineation threshold area on the simulated peak flow shows that the maximum and minimum differences (12% and 1%) occur at the threshold areas of 0.5% and 1%, respectively, while for threshold areas higher than 2% the difference in peak flow of the two sources is limited to 10%. Based on the results of this research, it is deduced that the effects of data resolution and stream network delineation threshold areas on the geomorphological parameter values and the performance of GIUH-based models are significant and should be considered when using SRTM DEMs in ungauged watersheds.
Keywords: SRTM DEM, topographic maps, rainfall-runoff Modelling, KW-GIUH, threshold area
INTRODUCTION
One of the most important steps in hydrological modelling is the extraction of the geomorphological parameters of watersheds. Nowadays, due to the use of digital elevation models (DEM), this extraction is simple. Currently, various sources are available to prepare DEMs for different applications, e.g., 1:25 000 and 1:50 000 topographic maps, 30 and 90 m SRTM DEMs, 30 m ASTER DEMs, and 1 km GTOPO30 DEMs. While the main source of DEMs is topographic maps based on ground surveys, these are not always at hand. Maathuis and Sijmons (2005) have indicated that the lack of adequacy, accuracy, and access to such sources is one of the most important problems faced by researchers, especially in developing countries. Over the past decades, satellite-based DEMs have found extensive use in hydrology and other earth sciences. These DEMs can be provided from different sources with a wide range of resolutions. With a DEM of appropriate resolution, watershed parameters can be computed with an acceptable accuracy.
Before the introduction of the SRTM DEMs, the only DEM sources covering the entire earth were the GTOPO30 and GLOBE (Hastings and Dunbar, 1998). Because of their low resolution (1 km x 1 km), they have not been extensively used in hydrological modelling (especially at small scales). Therefore, these have been replaced by DEMs from other sources. On the other hand, there are DEMs from sources such as LIDAR and SAR that enjoy an appropriate quality, but because of their high cost have limited application in rainfall-runoff modelling.
The introduction of SRTM DEMs, for all parts of the world, ended hydrologists' long wait for DEMs with an acceptable accuracy and resolution (Ludwig et al., 2006). The SRTM DEMs resolution is 30 m for the USA and 90 m for other countries. Uniformity of data, free access, and ease of use are the main reasons for the extensive application of these types of DEMs in rainfall-runoff modelling (Jensen, 1991; Wise, 2000; Rabus et al., 2003). Various algorithms, including watershed delineation and artificial stream network extraction, have been developed to derive basic characteristics of watersheds from DEM (Mark, 1984; Band, 1986; Jensen and Dominque, 1988; Li and Wong, 2010). Moreover, there are several studies which have shown the spatial accuracy of DEMs necessary for hydrological modelling (Gyasi et al., 1995; Baker et al., 2006). Tulu (2005), using the SWAT (Soil and Water Assessment Tool) software, showed the applicability of SRTM and ASTER DEMs in simulating daily discharges of the Malewa River basin, Kenya. He indicated that the average daily discharge, estimated with the help of information derived from SRTM DEMs, was lower than that derived based on ASTER DEMs. Hancock et al. (2005) used SRTM DEMs with a resolution of 10 and 90 m to extract the stream network and to simulate runoff in the Camp Creek watershed, Australia. The results indicated that both DEMs gave the same pattern for the stream network, but that the simulated runoff was different. Akbari et al. (2010) performed a comprehensive study in the Collang watershed, Malaysia, to compare the performance of SRTM DEMs and the DEMs derived from 1:25 000 topographic maps in extracting watershed characteristics. They found that for mountainous areas there are no significant differences among the watershed characteristics (area, perimeter, slope, etc.) extracted from the two DEMs. In this study, they indicated a high correlation between geomorpho-logical parameters derived from the two DEMs in the mountainous area. Alarcon and O'Hara (2006) used 3 DEM sources (30 m SRTM DEM, DEM from NAD (United States National Elevation Data), and USGS DEM) to extract the geomorpho-logical parameters of a watershed located in Saint Luis, USA. The results indicated that the sub-basin area and perimeter extracted from the SRTM DEMs was more accurate than that extracted from the NAD and USGS DEMs.
The most important aspect to consider when using SRTM DEMs for rainfall-runoff modelling is the adequacy/inadequacy of these DEMs relative to the required resolution for modelling. This aspect is very important in ungauged watersheds, where the accuracy of geomorphological information is essential for rainfall-runoff modelling. The main goal of the current study is to address this problem by analysing the effects of data resolution on the performance of rainfall-runoff models. The model used in this study is the KW-GIUH (Lee and Yen, 1997), which is a conceptual rainfall-runoff model. This model, which is explained in the following section, uses the geomorphological instantaneous unit hydrograph to simulate floods. The motive for using this model for rainfall-runoff modelling in this study was the importance of geomorphologic parameters in the model structure, which enables a more reliable comparison between the effects of topographic maps (TOPO DEM) and SRTM DEMs on model performance.
METHODS
Structure of the KW-GIUH model and its parameters
Geomorphological parameters are time-invariant, which makes them appropriate for rainfall-runoff modelling in ungauged watersheds (Himanshu, 2013). The geomorphological instantaneous unit hydrograph (GIUH) was first introduced by Rodriguez-Iturbe and Valdez (1979). These researchers represented flood hydrographs in the form of a travel-time probability distribution and by considering the geomorphological structure of watersheds. In this approach, the excess rainfall travels through different paths overland and in streams of different orders towards the watershed outlet. The method used by Rodriguez-Iturbe and Valdez (1979) is based on stream order; therefore, one can state that the reliable computation of raindrop travel-time in different phases of overland and stream flow plays an important role in the successive application of this method. Travel-time depends on flow velocity which varies both in space and time. Rodriguez-Iturbe and Valdez (1979) used regression equations to estimate the travel-time that could differ from one catchment to another. Lee and Yen (1997), instead of using empirical equations to estimate the travel-time within the catchment, represented a new model known as KW-GIUH based on the kinematic wave equation. The method used by Lee and Yen considers travel-time as a probabilistic quantification, but uses hydraulic methods for its calculation. Some reports are available on successful application of this model and modified versions of the model in different climates and topographic conditions: e.g. United States (Yen and Lee, 1997; Lee and Huang, 2013), Taiwan (Yen and Lee, 1997; Lee and Chang, 2005; Lee and Huang, 2013), Palestine (Shadeed et al., 2007), Japan (Chiang et al., 2007), India (Kumar, 2008), Russia (Lee et al., 2009), and Iran (Azizian and Shokoohi, 2014).
Based on the Horton-Strahler ordering scheme, the flow in a watershed of order Ω can be divided into different states such as overland and channel flow. In Fig. 1, xoi denotes the i-th order overland flow regions and xi denotes the i-th order channels, where i=1, 2, . . .  . The instantaneous unit hydrograph u(t) of a watershed can be expressed as follows (Rodriguez-Iturbe and Valdes 1979):
. The instantaneous unit hydrograph u(t) of a watershed can be expressed as follows (Rodriguez-Iturbe and Valdes 1979):
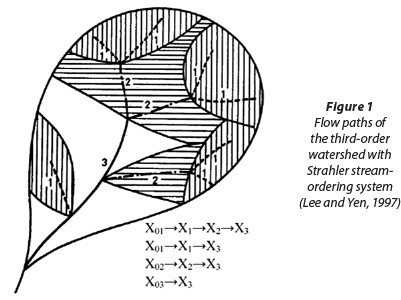
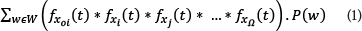
where:
fxoi is the travel-time probability density function in state
xoi with a mean value of T
fxj(t): is the travel-time probability density function in state
xj with a mean value of Txj
'*' denotes the convolution integral
P(w) is the probability of a drop of effective rainfall adopting path w
W is the space of flow paths given as W = (xoi, xi, xj, ...,x
) and the relationship between i and j means the subsequent state of the flow from an i-th order channel to a j-th order channel.
Figure 2 shows the runoff structure in which an i-th order sub-basin is conceptually simplified as a V-shaped plane.
Using kinematic-wave approximation, Lee and Yen (1997) derived travel-time equations for different orders of overland areas and streams. The runoff travel-time for a specified flow path can be estimated as follows (Lee and Yen, 1997):
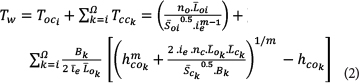
where:
Tw is the runoff travel-time for a specified flow path w
Toci is the mean runoff travel-time on the i-th order overland planes
Tcck is the mean runoff travel-time in the k-th order channels
Loi is the mean length of the i-th order overland flow
LCk is the mean length of the k-th order channel
ie is the excess rainfall intensity
Soi is the mean slope of i-th order overland flow
SCk is the mean slope of k-th order channel
Bk is the width of the k-th order channel
is the largest order of the watershed stream network
no and nc are the roughness coefficients for overland flow areas and channels, respectively
hcok is the inflow depth of the k-th order channel
The value of hcok is equal to zero for k=1 because no flow enters the channel from upstream. For 1<k<  , hcokcan be expressed as follows (Lee and Yen, 1997):
, hcokcan be expressed as follows (Lee and Yen, 1997):
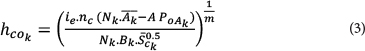
where:
Nk is the number of k-th order channels
is the mean area of the k-th order sub-basins
As shown in Eq. (2), a number of geomorphological parameters are required to estimate the runoff travel-time on overland areas and in channels. While these parameters can be obtained from a map, the channel width and roughness coefficient can only be defined by field investigation. To reduce the amount of field work required, the following relationship between channel width and watershed could be used (Lee and Yen, 1997; Lee et al., 2009):

where:
Bk is the k-th order channel width
B
is the channel width at the watershed outlet is the mean drainage area of order k
A is the total catchment area
Thus, the channel width at the watershed outlet is the only geometric feature required to be measured in the field. The roughness coefficient for overland and channel flow estimation could be obtained from field observation or by satellite image classification (Shuyou et al., 2010).
Pre-processing of DEMs and extraction of the stream network
DEMs should be free of sinks before extracting the stream network and other required parameters for hydrological modelling, in order to increase the accuracy of the DEM and guarantee model performance. A sink, a set of cells with the same height, creates holes in DEMs and breaks cell connectivity, and thus can introduce errors in flow tracing. In most cases, sinks appear in narrow valleys which have a width that is smaller than the DEM cell size. Moreover, because of interpolation errors, sinks may appear in low-slope areas. Archydro extension embedded in ArcView GIS is a common tool for the elimination of sinks. After this step, a flow-direction grid is extracted for each cell in the DEM. This grid is one of the key functions required to extract the hydrological characteristics of watersheds, and is actually a basis for all steps in watershed modelling (Tarboton, 1991). By using the flow-direction grid, the flow-accumulation grid is derived. In a flow-accumulation grid, the value of each cell represents the total number of cells draining into that cell. In this study, the D8 algorithm (the flow-tracing algorithm in the Archydro extension) is used to extract the flow-direction and flow-accumulation grids for a DEM of 50 m resolution. In a flow-accumulation grid, cells with the highest accumulation number represent streams and cells with a value of zero match the watershed boundaries. To extract an artificial stream network from a flow-accumulation map, it is necessary to precisely determine a threshold area, as the percentage of cells which pour into the target cell. Choosing a low threshold area leads to a high number of streams (smaller sub-basins), while choosing a high threshold area yields a smaller number of streams (larger sub-basins). In this study, two DEMs of 50 m resolution are constructed from a topographic map and by resampling of the SRTM DEMs. Finally, threshold areas of 0.25, 0.5, 1, 2, and 3% are used to extract the stream network and other geomorphological parameters.
Resampling is a process used to interpolate the new cell values of a raster during a resizing operation. There are many resampling methods available through a variety of platforms including GIS software. Each resampling method has strengths and weaknesses which should be considered carefully. Nearest neighbour (NN) resampling is a very commonly used method (Goldsmith, 2009), and was used in this paper to create a 50-m resolution DEM from the 90-m resolution SRTM DEMs.
Study area
The study area was the Kasilian watershed, a sub-basin of the Talar River watershed, in Mazandaran province in the north of Iran. This watershed, in the central Alborz mountain chain, is a mountainous area covered by forest. The Kasilian watershed, with an area of 67 km2 and a perimeter of 3 708 km, is drained by the Kasilian River, of 17 km length. The average slope of the watershed is 16.4%, and its elevation ranges between 1 100 and 2 650 m amsl. The location of Kasilian watershed and its DEM with 50 m resolution are shown in Fig. 3. The Valikbon hydrometric station, at X = 53° 06' and Y = 36° 01', is located at the watershed outlet and has been operated by Mazandaran Regional Water Board since 1975.
Data used for calibration and verification of the model
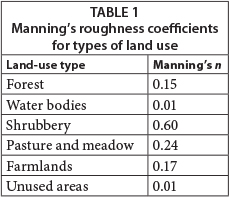
To evaluate KW-GIUH performance in the Kasilian watershed the recorded hydrographs at the Valikbon hydrometric station were used. For this gauge station there are only four reliable recorded hydrographs: two (1991/03/28 and 1987/10/09) were used for model calibration and the two others (2005/11/09 and 1993/09/03) were used for model verification. The major land-use types in the watershed were determined by field investigation. There are different methods for determining the roughness coefficient for overland and channel flow routing, among which the use of tabular data, introduced in literature by, e.g., Chaw (1959) and Yilmaz and Usul (2002). For this study the values suggested by Yilmaz and Usul (2002) (Table 1) were used. Manning coefficients for the channel and overland regions were estimated as 0.3 and 0.6, respectively.
The only important parameter in this model that requires calibration is the infiltration rate. In this model the index is used for net rainfall computation. The value of this parameter could be estimated by trial and error or by using recorded data.
RESULTS AND DISCUSSION
Geomorphological parameters required for the model
The geomorphological parameters of the study area are presented in Table 2.

In this study, to extract the watershed's geomorphological parameters, the threshold areas of 0.25, 0.5, 1, 2, and 3% were applied to the two types of DEM: namely, TOPO DEMs and SRTM DEMs. For all thresholds the trend of variations between the two DEM sources is almost identical except for the 1% threshold. In this section, the obtained results for the maximum and minimum thresholds (3% and 0.25%) are presented, and for the 1% threshold a comprehensive discussion can be found in the next sections. Only the geomorphological parameters derived at the threshold areas of 0.25 and 3% (for both DEM sources) are shown in Figs. 4-9.
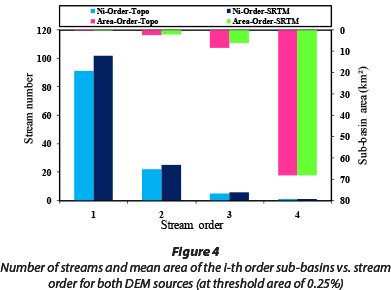
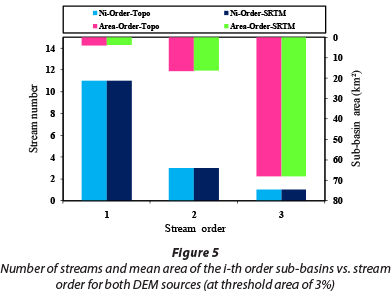
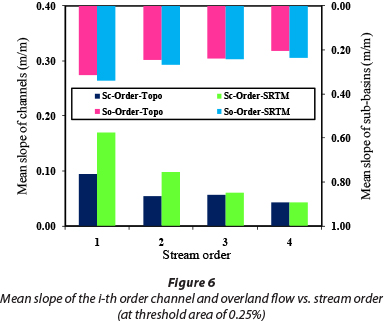
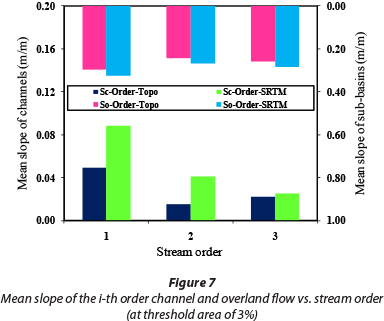
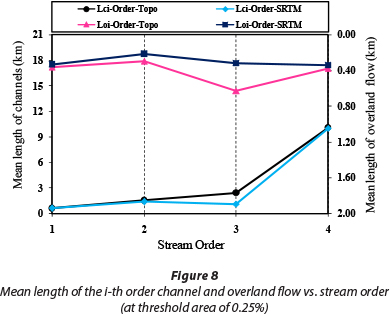
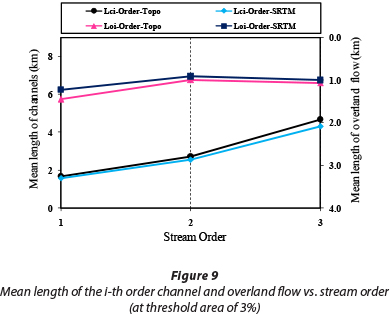
These figures show the variations in the effective parameters in the KW-GIUH model, in which Ni-Order and Area-Order represent the number of streams and mean area of i-th order sub-basins, respectively. Moreover, SC-Order and the SO-Order represent the mean slope of the i-th order channel and i-th order sub-basins, respectively. Also, Lci-Order and Loi-Order represent the mean length of the i-th order channel and i-th order overland flow, respectively. With respect to the number of streams, results indicate that at the threshold area of 3% there is no difference in the parameters derived from different DEM sources, while for lower threshold areas there is a significant difference, especially for streams of order 1 and 2 (Figs. 4 and 5). For example, at the threshold area of 0.25%, the difference for streams of order 1 and 2 is equal to 12.1% and 13.6%, respectively. This difference is important from the perspective of watershed flood generation potential. Studying the mean slope of the i-th order channel and i-th order sub-basins indicates that the values obtained from the SRTM DEMs are always higher than those obtained from the TOPO DEMs (Figs. 6 and 7). The slope of both overland and channel affects the travel-time of raindrops and flood wave velocity moving towards the basin outlet. Therefore, it can be expected that, due to the greater slope of the SRTM DEMs, the peak flow and slope of the hydrograph rising limb obtained from model application will be greater than that obtained for TOPO DEMs. This subject is discussed in more detail in the following sections. Furthermore, at almost all threshold areas the mean length of both i-th order channel and i-th order overland flow obtained from the TOPO DEM is higher than that from the SRTM DEMs (Figs. 8 and 9). This fact could increase the derived travel-time for channel and overland flow when using the TOPO DEM.
Model calibration and verification
One of the most valuable aspects of the KW-GIUH model, similarly to other geomorphological models, is that almost all of its parameters can be obtained from geomorphological properties of watersheds, and that model calibration requires only a few easy-to-find parameters. The only parameter in this model that requires calibration is the infiltration rate, i.e., the  index. The recorded hydrographs at the Valikbon hydrometric station were employed to determine this parameter. A trial-and-error process was used to calibrate the
index. The recorded hydrographs at the Valikbon hydrometric station were employed to determine this parameter. A trial-and-error process was used to calibrate the 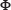 index; i.e., the calibration process was continued until the simulated hydrograph became approximately equal to the observed hydrographs. Figures 10-13 illustrate the results of calibration and verification. The model efficiency based on the Nash-Sutcliffe method is also presented in Table 3.
index; i.e., the calibration process was continued until the simulated hydrograph became approximately equal to the observed hydrographs. Figures 10-13 illustrate the results of calibration and verification. The model efficiency based on the Nash-Sutcliffe method is also presented in Table 3.
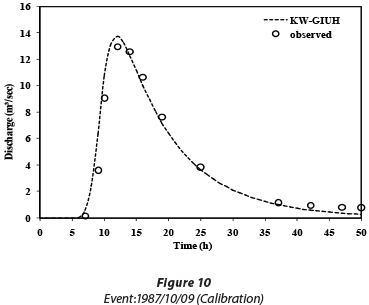

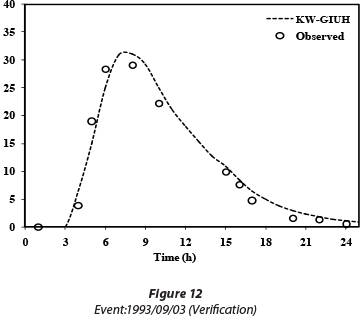
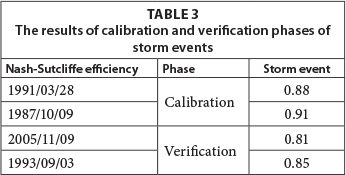
As the table and figures show, both in the calibration and verification phases, the model results conform with the observed data and indicate the acceptable performance of the KW-GIUH in simulating rainfall-runoff in the Kasilian watershed.
The effect of threshold area on model performance
In this study, to extract the stream network and other geomorphological parameters from the two DEM sources, while keeping DEM resolution constant, threshold areas of 0.25, 0.5, 1, 2, and 3% were used. Results indicate that the simulated peak flow is adversely affected by changing the thres hold area; i.e., the peak flow increases when decreasing the threshold area and decreases when threshold area increases. Additionally, with low threshold area, both the base time and the time to the peak of the hydrograph decrease. One of the most important issues for a flood warning system is the time to peak flow, which, according to the results of this study, can be influenced by the selection of a particular threshold area.
Changing the threshold area, the model displays different sensitivities to peak flow, time to peak and hydrograph base time. Maximum sensitivity is to peak flow, and then base time, while time to peak has the least influence on model performance. The simulated peak flow at the threshold area of 0.25% shows a 67% difference with the simulated peak flow at the threshold area of 3%. Also, the base time and the time to peak flow at the threshold area of 3% are 17 h and 1 h greater than that for 0.25%, respectively. Figure 14 shows the effect of different threshold areas on the shape and peak flow value of the simulated hydrograph.
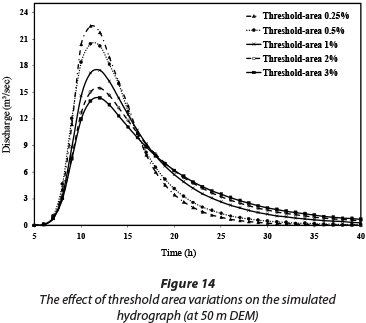
The slope of the hydrograph's rising limb is sensitive to the decrease/increase of threshold areas. As seen in Fig. 14, the rising limb's slope at the threshold area of 0.25% is 1.6 times greater than that of the rising limb at the threshold area of 3%. Actually, by increasing the stream formation threshold area, the number of extracted stream will decrease. For example in the studied watershed, the number of streams of order 1 at the threshold area of 0.25% is 91, while at the threshold area of 3% this is 11. From a hydraulic perspective, increasing the threshold area could increase the contribution of overland area (where resistance to flow is higher) to the total flow. Henceforth, regarding the governing equations in uniform flow such as the Manning equation, flow in sub-basins with low drainage density could be reduced, which will eventually decrease the simulated hygrograph's peak flow, and, based on the principle of mass balance, will increase the hydrograph base time. Similarly, by increasing the number of first-order streams, the effective rainfall will spend less time in each sub-basin and, after arriving in the stream, could move faster toward the watershed outlet. This phenomenon could reduce the time to peak and increase the slope of the hydrograph's rising limb.
Effect of DEM source on performance of KW-GIUH
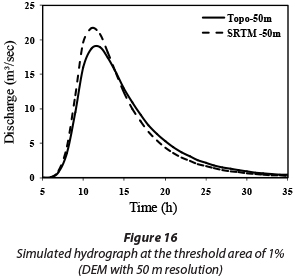
As mentioned above, two different DEM sources (topographic and SRTM) were applied to extract the watershed's geomorphological properties to define the required parameters of the KW-GUIH model. The results indicate that using different DEM sources has a significant effect on the simulated peak flow and also on the shape of the hydrograph. The effect of different sources on the simulated hydrograph at different threshold areas has been shown in Figs. 15 to 17. As can be seen, the simulated hydrographs based on the SRTM DEM have a higher peak flow than those obtained from the topographic maps.
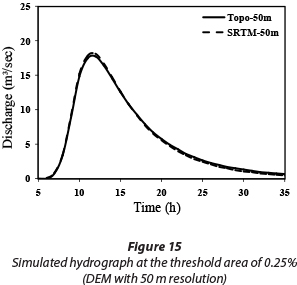

As mentioned in the 'methods' section, the mean length of overland flow derived for SRTM DEMs is less than that for TOPO DEMs. Reducing this parameter can decrease the travel-time for the overland flow to reach the channels. This then increases the velocity of excess rainfall towards the watershed outlet, which in turn decreases the hydrograph base time. Therefore, these two factors can be considered as the main reasons for the increase in the peak flow and slope of the hydrograph's rising limb for the SRTM DEM. The relationship between the mean lengths of overland flow for the two DEM sources is shown in Fig. 18. According to this figure, the mean length of the overland flow for the SRTM DEM, in most cases, is lower than the corresponding value fort he TOPO DEM.
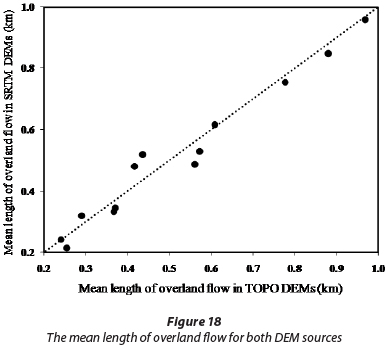
As illustrated in Fig. 19, the average slope of the sub-basins derived from the SRTM DEM is greater than the corresponding values estimated from the TOPO DEM. Considering this and the results for the length of overland flow, it can be deduced that the peak flow and also the slope of the hydrograph rising limb for the SRTM DEM will be greater than that for the TOPO DEM.
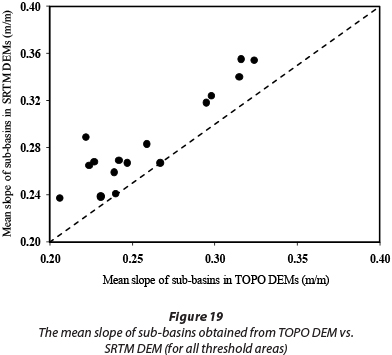
A notable result of the present study is the similarity of the hydrographs obtained from both sources at the threshold area of 1%. In other words, at this threshold area, DEM sources (data resolution) have no significant effects on the shape and peak flow of the hydrograph. This can be attributed to the similarity of important derived geomorphological parameters, such as sub-basin and channel slopes, for both DEM sources. While Fig. 19 shows that for threshold areas other than 1% there is a big difference in the slope of the sub-basins derived from the two different sources. Figure 20 also shows that they are approximately equal for the 1% threshold area. On this basis, it can be concluded that the effect of overland slope on flow routing is superior to the other parameters such as channel slope, channel length, and channel width.
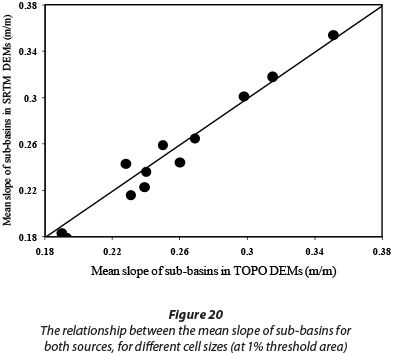
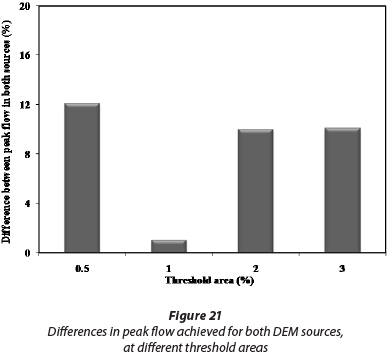
Figure 21 illustrates the effect of different threshold areas on the percentage peak flow difference. As observed, the highest and lowest difference occurs at the threshold areas of 0.5% and 1%, respectively. Furthermore, for threshold areas higher than 2% the peak flow difference between the two sources is limited to 10%.
CONCLUSION
This study intended to address two important issues in rainfall-runoff modelling. The first is the effects of data resolution on the simulated results of a rainfall-runoff model. The second is the applicability, adequacy and reliability of SRTM DEMs, which, due to their ease of access and being free of charge, have achieved a special place in rainfall-runoff modelling. The effects of the SRTM DEM on the derived geomorphological parameters and model performance were therefore compared with those obtained using the DEM interpolated from a 1:25000 topographic map. The GIUH (geomorphologic instantaneous unit hydrograph) models, which are employed extensively for rainfall-runoff modelling in ungauged watersheds, are based on geomorphological parameters. Given the aims of this study, and the considerable dependence of GIUH models on the geomorphological parameters of a watershed, a kinematic wave based GIUH, called KW-GIUH (Lee and Yen, 1997), was employed for this research.
Model performance, effects of different threshold areas for stream delineation (ranging from 0.25 to 3%) and the effects of different DEM sources on geomorphological parameters (such as overland and channel slope, overland and channel length, number of streams of different orders) were examined in a case study watershed in the north of Iran.
In comparison with other conceptual rainfall-runoff models, the calibration of KW-GIUH is very simple and is limited to the calibration of an infiltration index. The results of the calibration and verification phases show reasonable ability of the model to estimate the peak flow and the shape of the hydrograph. The average efficiency of the model based on the Nash-Sutcliff index, for the calibration and verification phases was about 89.5% and 84.5%, respectively. Analysing the derived geomorphological parameters from both DEM sources indicates that overland and channel slope in SRTM DEM are always higher than that derived from the TOPO DEM. Adversely, for almost all threshold areas, the mean length of the channels and overland flow derived from the TOPO DEM was higher than that derived from the SRTM DEM.
For both sources, by decreasing the stream delineation threshold area from 3 to 0.25%, the hydrograph peak flow increased and the base time decreased. This outcome could be due to the increase in the number of first-order streams and the decrease in the overland flow length and then travel-time in low-threshold areas. This could be important for flood warning systems, where the increase in the number of streams equals a faster movement of the flood and thus a reduced flood-warning lead time. By changing the threshold area, the model showed maximum sensitivity firstly to peak flow, then to base time and finally to time-to-peak-flow. According to the achieved results, the simulated peak flow at the threshold area of 0.25% is 67% greater than that for 3%. Also, base time and time-to-peak at a threshold area of 3% are, respectively, 17 h and 1 h greater than that for 0.25%. Studying the effect of different DEM sources on the simulated peak flow shows that the results for the SRTM DEM are greater than the corresponding values for the TOPO DEM. The maximum and minimum differences are at the threshold areas of 0.5% and 1%, respectively, while for threshold areas greater than 2% the difference in peak flow between the two sources is limited to 10%.
Based on the results of this research, it can be deduced that in ungauged watersheds, and where there is a lack of appropriate topographic maps, the SRTM DEMs could be useful for rainfall-runoff modelling and extracting the watershed geomorphologic characteristics. Combining the advantages of SRTM DEMs and the ability of the KW-GIUH model could be a useful tool for engineers in estimating the flood hydrograph in ungauged watersheds.
REFERENCES
AKBARI A, AZIZIAN A and OTHMAN F (2010) Practical use of SRTM digital elevation dataset in the urban-watershed modeling. J. Spat. Hydrol. 10 (2) 13-26. [ Links ]
ALARCON V J and O'HARA GG (2006) Using IFSAR and SRTM elevation data for watershed delineation of coastal watersheds. Proceedings MAPPS ASPRS Fall Conference, Measuring the Earth (Part II). American Society of Photogrammetry Remote Sensing, November 6-10, San Antonio, Texas, USA. [ Links ]
AZIZIAN A and SHOKOOHI AR (2014) DEM resolution and stream delineation threshold effects on the results of geomorphologic-based rainfall runoff models. J. Turk. J. Eng. Environ. Sci. 38 (1) 1-15. [ Links ]
BAKER C, LAWRENCE R, MONTAGNE C and PATTEN D (2006) Mapping wetlands and riparian areas using landsat ETM+ imagery and decision-tree-based models. J. Wetlands 26 465-474. [ Links ]
BAND LE (1986) Topographic partition of watersheds with digital elevation models. J. Water Resour. Res. 22 15-24. [ Links ]
GHYASI Y, WILLGOOSE GR and DETORCH FP (1995) Effect of vertical resolution and map scale of digital elevation model on geomorphological parameters used in hydrology. J. Hydrol. Process. 9 363-382. [ Links ]
HANCOCK G R (2005) The use of DEMs in the identification and characterization of catchment over different grid scales. J. Hydrol. Process. 19 1727-1749. [ Links ]
HASTINGS DA and DUNBAR PK (1998) Development and assessment of the global land one-km base elevation digital elevation model (GLOBE). ISPRS Arch. 32 (4) 218-221. [ Links ]
HIMANSHU SK, GARG N, RAUTELA S, ANUJA KM and TIWARI M (2013) Remote sensing and GIS applications in determination of geomorphological parameters and design flood for a Himalayan river basin, India. Int. Res. J. Earth Sci. 1 (3) 11-15. [ Links ]
JENSON SK and DOMINGUE JO (1988) Extracting topographic structure from digital elevation data for geographic information system analysis. J. Photogram. Eng. Remote Sens. 54 1593-1600. [ Links ]
JENSON SK (1991) Application of hydrologic information automatically extracted from digital elevation models. J. Hydrol. Process. 5 (1) 31-44. [ Links ]
KUMAR A (2008) Predicting direct runoff from hilly watershed using geomorphology and stream-order law ratios. J. Hydrol. Eng. 13 (7) 570-576. [ Links ]
LEE KT and YEN BC (1997) Geomorphology and kinematic-wave based hydrograph derivation. J. Hydraul. Eng. 123 (1) 73-80. [ Links ]
LEE KT and CHANG CH (2005) Incorporating subsurface-flow mechanism into geomorphology-based IUH modeling. J. Hydrol. 311 91-105. [ Links ]
LEE KT, CHEN NC and GARTSMAN BI (2009) Impact of stream network structure on the transition break of peak flows. J. Hydrol. 367 283-292. [ Links ]
LEE KT and HUANG JK (2013) Runoff simulation considering time-varying partial contributing area based on current precipitation index. J. Hydrol. 486 443-454. [ Links ]
LI J and WONG WS (2010) Effects of DEM sources on hydrologic applications. J. Comput. Environ. Urban Syst. 34 251-261. [ Links ]
LUDWIG R, TASCHNER S and MAUSER W (2006) Modeling floods in the Ammer catchment: limitations and challenges from a coupled meteo-hydrological model approach. J. Hydrol. Earth Syst. Sci. 7 (6) 833-847. [ Links ]
MAATHUIS B and SIJMONS K (2005) DEM from active sensors -shuttle radar topographic mission (SRTM). International Institute for Geo-Information Science and Earth Observation. Report W123. ITC, Holland. [ Links ]
MARK D (1984) Automated detection of drainage networks from digital elevation models. J. Cartograph. 21 168-178. [ Links ]
PARDO E and ATKINSON PM (2007) Modeling the semivariogram and crosssemivariogram required in downscaling cokriging by numerical convolution-deconvolution. J. Comput. Geosci. 33 (10) 1273-1284. [ Links ]
RABUS B, EINDER M, ROTH A and BAMLER R (2003) The shuttle radar topography mission: a new class of digital elevation models acquires by space borne radar. J. Photogram. Remote Sens. 57 241-262. [ Links ]
RODRIGUEZ-ITURBE I and VALDEZ JB (1979) The geomorphologic structure of hydrology response. J. Water Resour. Res. 15 (6) 1409-1420. [ Links ]
SHADEED S, SHAHEEN H and JAYYOUSI A (2007) GIS-based KW-GIUH hydrological model of semiarid catchments: the case of Faria catchment, Palestine. Arab. J. Sci. Eng. 32 (1C) 3-16. [ Links ]
SHUYOU C, LEE KT, HO J, LIU X, HUANG E and YANG K (2010) Analysis of runoff in ungauged mountain watersheds in Sichuan, china using kinematic-wave-based GIUH model. Science Press and Institute of Mountain Hazards and Environment. CAS and Springer-Verlag, Berlin. [ Links ]
TARBOTON DG, BRAS RL and RODRIGUEZ-ITURBE I (1991) On the extraction of channel networks from digital elevation data. J. Hydrol. Process. 5 81-100. [ Links ]
TULU MD (2005) SRTM DEM suitability in runoff studies. Master's Dissertation in ITC, Holland. [ Links ]
USUL N and YILMAZ M (2002) A pilot project for flood analysis by integration of hydrologic / hydraulic models and geographic information systems (in Turkish). METU. Ankara. Turkey. [ Links ]
WISE S (2000) Assessing the quality for hydrological applications of digital elevation models derived from contours. J. Hydrol. Process. 14 1909-1929. [ Links ]
WOODING RA (1965) A hydraulic model for the catchment-stream problem. J. Hydrol. 3 254-267. [ Links ]
YEN BC and LEE KT (1997) Unit hydrograph derivation for ungauged watersheds by stream order laws. J. Hydrol. Eng. 2 (1) 1-9. [ Links ]
Received 24 January 2014
Accepted in revised form 10 December 2014
* To whom all correspondence should be addressed. 00982833901148; e-mail: shokoohi@eng.ikiu.ac.ir













